Статистические методы и модели - Костин В.Н., Тишина Н.А

Рассмотрим двусторонний критерий. Для этого α = 0,1 делим пополам. Для двустороннего критерия выдвигаем две гипотезы

H0 :σ~12 =σ~22 ;

H1 :σ~12 ≠σ~22.

Если оценка попадает внутрь интервала, то исходные данные не противоречат гипотезе Н0.

Для двустороннего критерия мы имеем следующую статистику Фи-

шера.

H0

Рисунок 2.8 – Распределение Фишера для двустороннего критерия

По таблице Фишера определим:

Получили двусторонний интервал меньше 0,37 и больше 2,67. Наша оценка находится в интервале принятия решения.

41

2.5 Оценка однородности дисперсии

Оценка однородности дисперсии это оценка принадлежности дисперсии одной генеральной совокупности. Данная оценка производится по

критерию Кохрена. Имеется К выборок σ~12,σ~22, ...,σ~k2 . Несмотря на то, что

все дисперсии различны, они все из одной выборки. Необходимо оценить однородность дисперсий. Кохрен ввел статистику G.

G = max{σ~i2 }.

∑k σ~i2

i=0

Величина G - имеет распределение Кохрена (приложение A). Для применения распределения Кохрена необходимо, чтобы выборки по всем дисперсиям были одинаковы.

По заданному уровню значимости находим Gкр. Рассчитываем Gоп опытное значение. Если Gоп >Gкр - то гипотеза отвергается.

Пример № 6. Имеем четыре независимых выборки (объемом n = 17) из нормальной совокупности σ~2 :0,21; 0,25; 0,34; 0,40. При доверительной вероятности α =0,05 проверить гипотезу однородности дисперсии

По таблице Кохрена для числа степеней свободы n = 17 – 1 = 16 и количества в выборке N = 4 дисперсий находим Gкр = 0,4366. Так как, Gоп <Gкр , то гипотеза об однородности принимается.

2.6 Оценка сомнительных результатов

Допустим, получили результаты из одной генеральной совокупности, для которой некоторые результаты выборки вызывают сомнение. Возникает вопрос: какие наблюдения оставить в выборке, а какие выбросить? Для решения данной задачи существует ряд критериев. Рассмотрим их на примерах.

1 Провели пять выстрелов из гаубицы, имеем следующий ряд точек попадания снарядов по дальности [M]

42

видим, среднее квадратичное (сигма) отличается на порядок.

1 Критерий об оценке сомнительных результатов предполагает, что σ Г - генеральной совокупности известная величина. Вводится статистика

t = xmax − m~ x .

σ Г

Данная статистика распределена не по нормальному закону, но похожа на нормальный закон (рисунок 2.9).

Нормируем случайную величину

n

Запишем через нормальный закон распределения вероятность попадания в критическую область

Рисунок 2.9 – Нормальный закон распределения

43

По заданному уровню значимости находим zкр (смотреть приложение Д). Рассчитываем tоп опытное значение. Если tоп > tкр, то сомнительный ре-

зультат отбрасывается

2 Если σx генеральной совокупности неизвестно, то в этом случае вводим статистику, которая принадлежит критерию Смирнова – Гребса

t = xmaxσ~−x m~x .

Распределение Смирнова – Гребса имеет оценку

табличное критическое значение равно tкр = 2,2 .

Получили опытное значение меньше критического, значит, подозрительный результат следует оставить в выборке.

3 Распределение Смирнова – Гребса по одному выбросу. Вводится статистика Гребса

46

Если Gоп попадает в критическую область, то аномальный результат

отбрасываем.

4 Статистика Титьена – Мура позволяет проводить оценку сразу нескольких выбросов. Определяется опытное значение:

тельных результатов.

Оценка Титьена-Мура имеет большое распределение, входом в таблицу является α , количество выбросов k и объем выборки n.

Пример № 6. Имеются данные – временные затраты на выполнение однотипных работ для десяти человек (таблица 2.4).

Таблица 2.4

персии σ x2 . Есть ли основание для исключения последнего результата из вы-

борки. Проведем оценки по следующим критериям:

1 По критерию Смирнова определяем опытные значения

tкр = 2,3.

Вывод: Результат t =18 – проходит с малой надежностью. 2 По критерию Гребса имеем

45

=1236,96,4 = 0,356,

При уровне значимости α =0,025 по таблице Гребса (приложение Е) определяем критическую область Gкр = 0,3526 . Функция Гребса представлена

на рисунке 2.10.

1

Gкр

0,356

G

Рисунок 2.10 – Функция Гребса

По критерию Гребса результат также проходит с малой надежностью. 3 По критерию Титьена-Мура проверим следующие результаты:

а) если выбросить последний результат t =18 , то получим Zоп = 0,356 . По таблице Титьена-Мура (приложение Ж) при α =0,05 находим критическое значение Zкр =0,418 следовательно, результат необходимо выбро-

сить, а при α =0,01 получаем Zкр =0,28, поэтому результат нужно оставить. б) Определим опытное значение статистики Титьена-Мура

α =0,01, Zкр =0,142.

Вывод: при α =10 % и α = 5 % – результат 15 и 18 необходимо выбросить из выборки. Если α =1% , то результаты 15 и 18 необходимо оставить.

46

3 Обработка результатов эксперимента методом регрессионного анализа

3.1 Зависимость между случайными величинами

При изучении процессов функционирования сложных систем приходится иметь дело с целым рядом одновременно действующих случайных величин. Для уяснения механизма явлений, причинно-следственных связей между элементами системы и т.д., по полученным наблюдениям мы пытаемся установить взаимоотношения этих величин.

В математическом анализе зависимость, например, между двумя величинами выражается понятием функции

y=f(x),

где каждому значению одной переменной соответствует только одно значение другой. Такая зависимость носит название функциональной.

Гораздо сложнее обстоит дело с понятием зависимости случайных величин. Как правило, между случайными величинами (случайными факторами), определяющими процесс функционирования сложных систем, обычно существует такая связь, при которой с изменением одной величины меняется распределение другой. Такая связь называется стохастической, или вероятностной. При этом величину изменения случайного фактора Y, соответствующую изменению величины Х, можно разбить на два компонента. Первый связан с зависимостью Y от X, а второй с влиянием "собственных" случайных составляющих величин Y и X. Если первый компонент отсутствует, то случайные величины Y и X являются независимыми. Если отсутствует второй компонент, то Y

иX зависят функционально. При наличии обоих компонент соотношение между ними определяет силу или тесноту связи между случайными величинами Y

иX.

Существуют различные показатели, которые характеризуют те или иные стороны стохастической связи. Так, линейную зависимость между случайными величинами X и Y определяет коэффициент корреляции.

47

Линейная вероятностная зависимость случайных величин заключается в том, что при возрастании одной случайной величины другая имеет тенденцию возрастать (или убывать) по линейному закону. Если случайные величины X и Y связаны строгой линейной функциональной зависимостью, например,

y=b0+b1x1,

то коэффициент корреляции будет равен r = ±1; причем знак соответствует знаку коэффициента b1 .Если величины X и Y связаны произвольной стохастической зависимостью, то коэффициент корреляции будет изменяться в пределах

−1< r < +1.

Следует подчеркнуть, что для независимых случайных величин коэффициент корреляции равен нулю. Однако коэффициент корреляции как показатель зависимости между случайными величинами обладает серьезными недостатками. Во-первых, из равенства r = 0 не следует независимость случайных величин X и Y (за исключением случайных величин, подчиненных нормальному закону распределения, для которых r = 0 означает одновременно и отсутствие всякой зависимости). Вовторых, крайние значения r = ±1 также не очень полезны, так как соответствуют не всякой функциональной зависимости, а только строго линейной.

Полное описание зависимости Y от X , и притом выраженное в точных функциональных соотношениях, можно получить, зная условную функцию распределения F[Y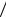 X = x].

Следует отметить, что при этом одна из наблюдаемых переменных величин считается неслучайной. Фиксируя одновременно значения двух случайных величин X и Y, мы при сопоставлении их значений можем отнести все ошибки лишь к величине Y. Таким образом, ошибка наблюдения ∆y будет складываться из собственной случайной ошибки величины Y и из ошибки сопоставления, возникающей из-за того, что с величиной Y сопоставляется не совсем то значение X, которое имело место на самом деле.

Однако отыскание условной функции распределения, как правило, оказывается весьма сложной задачей. Наиболее просто исследовать зависимость между Х и Y при нормальном распределении Y, так как оно полностью определяется математическим ожиданием и дисперсией. В этом случае для описания зависимости Y от X не нужно строить условную функцию распределения, а достаточно лишь указать, как при изменении параметра X изменяются математическое ожидание и дисперсия величины Y.

Таким образом, мы приходим к необходимости отыскания только двух функций:

48

Зависимость условной дисперсии D [Y/X=x] от параметра Х носит название сходастической зависимости. Она характеризует изменение точности методики наблюдений при изменении параметра и используется достаточно редко.

Зависимость условного математического ожидания M[Y/x=x] от X носит название регрессии, она дает истинную зависимость величин Х и У, лишенную всех случайных наслоений. Поэтому идеальной целью всяких исследований зависимых величин является отыскание уравнения регрессии, а дисперсия используется лишь для оценки точности полученного результата.

3.2 Обработка результатов пассивного эксперимента методом регрессионного анализа

3.2.1 Основные понятия классического регрессионного анализа

В пассивном эксперименте исходная информация о функционировании сложной системы может быть получена путем непрерывной или дискретной фиксации уровней исследуемых входных факторов и выходных параметров системы в условиях ее нормального функционирования. В данном случае, как уровни, так и сочетания уровней всех входных факторов в каждый момент времени будут являться случайными величинами. Случайными величинами будут являться и выходные параметры системы. При проведении пассивного эксперимента исследователь каждому сочетанию уровней всех входных факторов должен поставить в соответствие текущий уровень выходных параметров системы. Полученная таким образом информация может быть представлена в виде следующей таблицы.

Таблица 3.1 – Результаты пассивного эксперимента

Выходные параметры системы ys стохастически связаны с входными факторами xi. В общем виде, эту связь можно представить выражением:

где i=1,k;

49

ε– аддитивная помеха, то есть величина, учитывающая случайные ошибки измерений, случайные шумы, влияние неучтенных факторов.

Данную аналитическую зависимость принято называть математической моделью системы, полученной по результатам пассивного эксперимента. Так как математическая модель вида (3.3) находится для каждого выходного параметра системы y1, y2, ..., ys, ..., yr в отдельности, то в дальнейшем будем рассматривать способ ее нахождения лишь в общем виде для одного выходного параметра y.

Выше было отмечено, что истинную зависимость величин X и Y характеризует зависимость условного математического ожидания M[Y/X=x] от параметра. Следовательно, математическую модель (3.3) целесообразно искать в виде уравнения регрессии. Если принять условие, что математическое ожидание аддитивной помехи

M[ε]=0,

то условное математическое ожидание выходного параметра y будет совпадать со значением функции ϕ(xi):

где ϕ(xi) – функция регрессии.

Условное математическое ожидание M[Y/Xi=xi], как правило, зависит не только от входных факторов xi, но и от некоторых параметров βi, тогда

M[Y/Xi=xi]=y=ϕ(xi, βi). (3.5)

В зависимости от того, как данные параметры βi входят в функцию регрессии, модели (3.5) делятся на линейные и нелинейные (по параметрам). Мы будем рассматривать только линейные регрессионные модели.

Точное уравнение регрессии можно получить, только зная M[Y/Xi=xi] для всех допустимых значений переменной xi.

Практически, при проведении экспериментальных исследований такая ситуация невозможна, так как даже отдельные значения M[Y/Xi=xi] не могут быть найдены точно. В связи с этим мы можем искать лишь уравнения приближенной регрессии, оценивая величину и вероятность этой приближенности. Уравнение приближенной регрессии будем записывать в виде:

50