Статистические методы и модели - Костин В.Н., Тишина Н.А

Математическое ожидание и дисперсия для суммы равномерных законов на интервале [a, в] имеет вид:

Если выбрать интервал [0,1], то математическое ожидание и дисперсия будут оцениваться по зависимостям:

Для получения последовательности нормально распределенных случайных величин с заданными M (x) и D ( x ) мы должны использовать величину Zi, которая будет являться нормально распределенной случайной величиной, с параметрами N(0,1). Тогда случайная величина xi будет определять-

ся по формуле:

xi = M (x)+σ(x) Zi .

отсюда нормированная величина будет иметь вид:

При m → ∞ случайная величина Zi стремится к стандартной нормально распределенной случайной величине с нулевым математическим ожиданием и дисперсией равной 1.

На практике обычно берут m = 12, поэтому:

11

Таким образом, моделирование случайной величины χ =N( a,σ ), имеющее нормальное распределение с параметрами аи σ , основано на использовании зависимости:

1.3 Приближенный способ формирования случайной величины с произвольной функцией распределения

Случайная величина может быть задана дискретно. В этом случае интеграл от закона распределения не берется.

1 Способ формирования случайной дискретной величины. Предположим, что случайная величина x принимает следующие зна-

чения

n

Условие нормировки ∑pi =1.

i=1

Для реализации дискретного распределения берется отрезок единичной длины и разбивается на интервалы

y1 = p1,

Длина отрезков пропорциональна вероятности. Тогда вероятность того, что случайная величина примет случайное значение от a до в

в

p(a < x <в)= ∫ f (x)dx =в−а,

a

при условии, что внутри каждого интервала плотность распределения равна единице.

Вероятность того, что x примет значение yi−1 до yi будет равно

p(yi−1 < x < yi )= yi − yi−1 = p1 + p2 +...+ pi − p1 − p2 −...− pi−1 = pi ,

12

то есть, равна длине интервала yi − yi−1 или вероятности.

Формулируем случайную величину R, равномерно распределенную на интервале [0,1]. Определяем в какой интервал попадет R, затем по интервалу определяем вероятность и присваиваем ей значение, которое определено исходными данными (рисунок 1.5).

зом, можно формировать любое дискретное распределение.

2 Способ формирования случайной величины x , заданной непрерывной функцией.

Допустим, непрерывная функция распределения может быть получена опытным путем, а аналитически описать ее не представляется возможным или результат описания опытного распределения не удовлетворяет исследователя. В этом случае используют данный способ.

На первом этапе определяем интервал изменения случайной величины до xmax . Весь интервал изменения случайной величины делится на n

равных интервалов ∆χ (рисунок 1.6)

∆χ = xmax −xmin .

n

f (x)

Рисунок 1.6 – Произвольный закон распределения

На каждом интервале строим криволинейную трапецию, основание которой является ∆x , а верхняя часть кривая функции. В виду того, что ∆x → 0 , тогда площадь криволинейной i-ой трапеции определяется выражением:

13

На каждом интервале строим прямоугольник, площадь которого эквивалентна площади элементарной криволинейной трапеции. Высота прямоугольника равна

Hi = ∆Six .

Теперь необходимо нормировать всю площадь под кривой из условия,

что

Сумма всех площадей

n

S = ∑i=1 Si .

Нормализацию проводим по зависимости

Ωi = SSi ,

тогда, если сложить

n

∑Ωi =1.

i=1

Единичный интервал [0,1] разбиваем на интервалы, соответствующие нормированным площадям Ωi . Вероятность того, что случайная величина x

попадет в интервал p (yi−1 < x < yi )=Ωi .

Внутри каждого интервала случайная величина будет распределена равномерно при условии, что ∆x →0 .

Формирование случайной величины по заданному закону производится следующим образом:

1Генерируется случайная величина R, определяется интервал i, в котором приобретает значение формируемая случайная величина.

2Производится вторичное генерирование случайной величины R. Учитывая, что внутри каждого интервала случайная величина распределена равномерно, то по формуле равновероятного распределения получим

14

1.4 Общие сведения о цепях Маркова

1.4.1 Основные понятия марковских процессов

Марковские случайные процессы названы по имени выдающегося русского математика А.А. Маркова (1856-1922), впервые начавшего изучение вероятностной связи случайных величин и создавшего теорию, которую можно назвать “динамикой вероятностей”. В дальнейшем основы этой теории явились исходной базой общей теории случайных процессов, а также таких важных прикладных наук, как теория диффузионных процессов, теория надежности, теория массового обслуживания и т.д. В настоящее время теория марковских процессов и ее приложения широко применяются в самых различных областях таких наук, как механика, физика, химия и другие.

Благодаря сравнительной простоте и наглядности математического аппарата, высокой достоверности и точности получаемых решений особое внимание марковские процессы приобрели у специалистов, занимающихся исследованием операций и теорией принятия оптимальных решений.

Несмотря на указанную выше простоту и наглядность, практическое применение теории марковских цепей требует знания некоторых терминов и основных положений, на которых следует остановиться.

Марковские случайные процессы относятся к частным случаям случайных процессов (СП). В свою очередь, случайные процессы основаны на понятии случайной функции (СФ).

Случайной функцией называется функция, значение которой при любом значении аргумента является случайной величиной (СВ). По-иному, СФ можно назвать функцию, которая при каждом испытании принимает какойлибо заранее неизвестный вид.

Такими примерами СФ являются: колебания напряжения в электрической цепи, скорость движения автомобиля на участке дороги с ограничением скорости, шероховатость поверхности детали на определенном участке и так далее.

Как правило, считают, что если аргументом СФ является время, то процесс, основанный на такой функции, называют случайным. Существует и другое, более близкое к теории принятия решений, определение СП. При этом под случайным процессом понимают процесс случайного изменения состояний какой-либо физической или технической системы по времени или какому-либо другому аргументу.

Нетрудно заметить, что если обозначить состояние Si и изобразить зависимость Si (t), то такая зависимость и будет случайной функцией.

СП классифицируются по видам состояний Si и аргументу t. При этом

СП могут быть с дискретными или непрерывными состояниями или временем. Например, любой выборочный контроль продукции будет относиться к СП с дискретными состояниями ( S1 - годная, S2 - негодная продукция) и

дискретным временем (t1 , t2 - времена проверки). С другой стороны, случай

15

отказа любой машины можно отнести к СП с дискретными состояниями, но непрерывным временем. Проверки термометра через определенное время будут относиться к СП с непрерывным состоянием и дискретным временем. В свою очередь, например любая осциллограмма, будет записью СП с непрерывными состояниями и временем.

Кроме указанных выше примеров классификации СП существует еще одно важное свойство. Это свойство описывает вероятностную связь между состояниями СП. Так, например, если в СП вероятность перехода системы в каждое последующее состояние зависит только от предыдущего состояния, то такой процесс называется процессом без последействия (рисунок 1.7).

Зависимость Pi/i+1 = f (Si ) называют переходной вероятностью, часто

говорят, что именно процесс без последействия обладает марковским свойством, однако, строго говоря, здесь есть одна неточность. Дело в том, что можно представить себе СП, в котором вероятностная связь существует не только с предшествующими, но и более ранними ( Si−1, Si−2 ) состояниями, то есть

pi/i+1 = f (Si )

Рисунок 1.7 – Схема процесса без последействия

Такие процессы также рассматривались А.А. Марковым, который предложил называть их в отличие от первого случая (простой цепи) - сложной цепью. В настоящее время теория таких цепей разработана слабо и обычно применяют так называемый процесс укрупнения состояний, путем математических преобразований, объединяя предшествующие состояния в одно.

Это обстоятельство должно обязательно учитываться при составлении математических моделей принятия решений.

Остановимся подробнее на понятии “марковской цепи”. Отметим, вопервых, что случайный процесс с дискретными состояниями и временем называется случайной последовательностью.

Если случайная последовательность обладает марковским свойством, то она называется цепью Маркова.

С другой стороны, если в случайном процессе состояния дискретны, время непрерывно и свойство последействия сохраняется, то такой случай-

ный процесс называется марковским процессом с непрерывным временем.

Еще одним условием описания модели является требование, чтобы вероятности переходов из состояния в состояние подчинялись экспоненци-

16

альному закону, то есть переход из состояния в состояние представляет собой пуассоновский поток.

Различают марковские системы по количеству состояний, в которых находится система: системы с конечным состоянием и системы с бесконечным состоянием.

Марковский СП называется однородным, если переходные вероятности Pi/i+1 остаются постоянными в ходе процесса и не зависит от номера ис-

пытания.

Модель марковской цепи может быть представлена в виде ориентированного взвешенного графа (рисунок 1.8).

P23

S2

P12

Рисунок 1.8 – Ориентированный взвешенный граф

Вершины графа обозначают состояние Si , а дуги – переходные веро-

ятности.

Множество состояний системы марковской цепи, определенным образом классифицируется с учетом дальнейшего поведения системы.

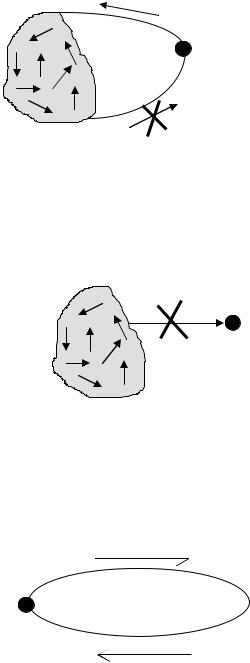
1 Невозвратное множество (рисунок 1.9).

Рисунок 1.9 – Невозвратное множество

В случае невозвратного множества возможны любые переходы внутри этого множества. Система может покинуть это множество, но не может вернуться в него.

17

2 Возвратное множество (рисунок 1.10).

Рисунок 1.10 – Возвратное множество

В этом случае также возможны любые переходы внутри множества. Система может войти в это множество, но не может покинуть его.

3 Эргодическое множество (рисунок 1.11).

Рисунок 1.11 – Эргодическое множество

В случае эргодического множества возможны любые переходы внутри множества, но исключены переходы из множества и в него.

4 Поглощающее множество (рисунок 1.12)

Рисунок 1.12 – Поглощающее множество

При попадании системы в это множество процесс заканчивается. Кроме описанной выше классификации множеств различают состоя-

ния системы:

18

а) существенное состояние (рисунок 1.13): возможны переходы из Si в S j и обратно;

Pij >0

Si 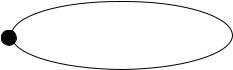S j

Pij >0 ;

Рисунок 1.13 – Существенное состояние

б) несущественное состояние (рисунок 1.14): возможен переход из Si в S j , но невозможен обратный.

Pij >0

Рисунок 1.14 – Несущественное состояние

В некоторых случаях, несмотря на случайность процесса, имеется возможность до определенной степени управлять законами распределения или параметрами переходных вероятностей. Такие марковские цепи называются управляемыми. Очевидно, что с помощью управляемых цепей Маркова (УЦМ) особенно эффективным становится процесс принятия решений, о чем будет сказано впоследствии.

Основным признаком дискретной марковской цепи (ДМЦ) является детерминированность временных интервалов между отдельными шагами (этапами) процесса. Однако часто в реальных процессах это свойство не соблюдается и интервалы оказываются случайными с каким-либо законом распределения, хотя марковость процесса сохраняется. Такие случайные последовательности называются полумарковскими.

Кроме того, с учетом наличия и отсутствия тех или иных, упомянутых выше, множеств состояний марковские цепи могут быть поглощающими, если имеется хотя бы одно поглощающее состояние, или эргодическими, если переходные вероятности образуют эргодическое множество.

19

В свою очередь, эргодические цепи могут быть регулярными или циклическими. Циклические цепи отличаются от регулярных тем, что в процессе переходов через определенное количество шагов (циклов) происходит возврат в какое-либо состояние. Регулярные цепи этим свойством не обладают. Если просуммировать все вышесказанные определения, то можно дать следующую классификацию марковских процессов (рисунок 1.15):

простые сложные

поглощающие эргодические

регулярные циклические

Рисунок 1.15 – Классификация марковских процессов

1.4.2 Переходные вероятности. Матрица перехода

Переход системы из состояния в состояние будем рассматривать в дискретные моменты времени.

Система считается заданной, если заданы два условия.

1 Заданы вероятности возможных состояний системы Pi (t) . Вероят-

ности нахождения в этих состояниях – это доли времени нахождения в каждом состоянии. Имеется вектор начальных вероятностей начального состояния системы

Pi (0 ) = ( P01 , P02 , ... , P0 n ) ,

описывающий начальное состояние системы.

2 Заданы условные вероятности переходов из состояния в состояние за время ∆t . Это вероятность перехода Pik (∆t) из i-го в k-ое состояние за

время ∆t (причем, чем больше ∆t , тем больше вероятность). Данные вероятности переходов задаются с помощью матрицы, которая имеет следующий вид:

20