2.3. Применение идей, лежащих в основе мар

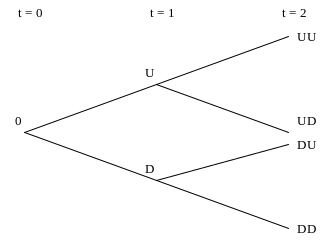
Как только сценарное дерево построено, его можно использовать для разбиения денежных потоков какого-либо проекта на части, соответствующие тому или иному «событию», ради последующей оценки с применением принципа стоимостной аддитивности. В этих целях вначале для каждого «события» определяют «единичный денежный поток», то есть денежный поток единичной величины, который появляется в момент времени, соответствующий заданному «событию», в том и только том случае, если это событие состоялось. (Например, рассмотрим событие UD на сценарном дереве, представленном на Рис.1. Единичный денежный поток UD появляется в периоде t = 2. Он имеет величину $1, если событие UD имеет место, и $0, если событие UD не произошло.) Назовём финансовое требование на такой единичный денежный поток «элементарным условным активом», привязанным к событию UD («э.у. активом UD»).

Требование на любой денежный поток в любой заданный момент времени может быть точно сымитировано путём составления портфеля из элементарных условных активов, соответствующих событиям, которые могут случиться в этот момент. Доля каждого э.у. актива в этом имитирующем портфеле задана величиной данного денежного потока в случае, если соответствующее событие действительно случится.

В качестве примера снова рассмотрим сценарное дерево на Рис.1, а также денежный поток периода t = 2, который примет значение $20, если наступит событие UU, $12 – если случится событие UD, $15 – если случится событие DU, и $9 – если случится событие DD. Требование на такой денежный поток может быть сымитировано путём составления портфеля, в который войдут 20 э.у. активов UU, 12 э.у. активов UD, 15 э.у. активов DU и 9 э.у. активов DD.

Предположим, что мы способны дать оценку текущей стоимости э.у. актива, привязанного к любому событию на сценарном дереве. Назовём эту оценку «ценой события» для каждого события. Тогда стоимостную оценку требования на любой денежный поток можно провести путём стоимостной оценки соответствующего имитирующего портфеля, состоящего из э.у. активов. Оценка осуществляется на основе принципа стоимостной аддитивности. Во-первых, для каждого события на сценарном дереве, имеющего отношение к данному денежному потоку, рассчитывается произведение цены события на величину денежного потока в случае наступления этого события. Затем эти произведения складываются.

Рис.1. Простое двухпериодное дерево сценариев для рынка нефти.

Например, предположим, что текущие рыночные цены э.у. активов (наблюдаемые либо рассчитанные) для четырёх событий периода t = 2, изображённых на сценарном дереве на Рис.1, равны

$0,081225 для события UU,

$0,189525 для события UD,

$0,189525 для события DU, и

$0,44225 для события DD.

Тогда текущая ценность требования на денежный поток, определённый двумя абзацами выше, равна:

20 × $0,081225 + 12 × $0,189525 + 15 × $0,189525 + 9 × $0,442225 =

= $1,624500 + $2,274300 + $2,824875 + $3,980025 = $10,7037.