4.4.2. Цены элементарных условных активов

В соответствии с рекомендациями Раздела 3.6, цену каждого э.у. актива можно разложить на фактор дисконта времени и скорректированную на риск вероятность.

В наших примерах реальные величины факторов дисконта времени определены на основе предполагаемой постоянной безрисковой ставки дисконта в 3% годовых (с непрерывным начислением). Для перевода реальных денежных потоков в номинальные и обратно предполагается, как и в первой статье, постоянный темп инфляции в 3% годовых (с непрерывным начислением), то есть номинальная безрисковая ставка дисконта времени равна 6% годовых (с непрерывным начислением). В наших моделях ставки дисконта времени считаются заданными детерминистски, без присутствия какого-либо элемента непределённости.

Поправка величин денежных потоков на риск будет осуществляться исходя из предполо­жения о наличии независимой от времени цены риска в составе цены на нефть. Как было отмечено в Разделе 4.2, величина этой цены риска принята в каждой из рассматриваемых моделей такой, чтобы краткосрочный дисконт на риск оставался одним и тем же для разных моделей внутри каждой из двух подборок моделей: 4% годовых для моделей перманентного шока и 10,5% годовых для моделей возврата к среднему.

Для того чтобы найти скорректированное на риск распределение вероятности на сценар­ном дереве (которое теперь рассматривается в непрерывном времени, с непрерывной сменой событий), надо для каждой модели цены на нефть пройти через те же самые шаги, через которые мы проходили, рассматривая дискретное сценарное дерево в Разделе 3.

Для каждого события на сценарном дереве в дискретном времени может быть подобрана инвестиционная стратегия, в соответствии с которой из безрисковых активов и требова­ний на поставку газа составляется начальный портфель, с последующей торговлей данны­ми активами по мере поступления новой информации, так что, вне зависимости от того, какой именно сценарий будет реализован, данная стратегия обеспечивает в точности те же платежи, что и э.у. актив, который эта стратегия имитирует. Для динамического имитиро­вания на сценарном дереве, показанном на Рис.1, достаточно торговли двумя активами, так как каждое новое ветвление на этом дереве содержит не более двух путей. С помощью одного из активов (требование на безрисковый денежный поток) процесс имитирования продлевается во времени, а с помощью другого (требование на поставки газа) мы про­водим различие между двумя направлениями движения, возможными из каждого отдельно взятого узла сценарного дерева.

Если сценарное дерево строится в непрерывном времени с непрерывным развитием собы­тий, то его ветвление также имеет непрерывный характер, хотя изменения и локализованы в вероятностном смысле. Поэтому необходимо предположить возможность непрерывной торговли активами, обеспечивающей динамическое имитирование денеж­ных потоков по проекту. При этом оказывается, что нам по-прежнему требуется лишь один актив для того, чтобы продвигать процесс построения имитирующего портфеля далее во времени. Однако, по причине непрерывного характера торговли и локализованных изменений ценовых прогнозов, число активов, которое требуется для отслеживания непрерывного ветвления, задано теперь числом нормально распределённых переменных, необходимых для описания этого ветвления⁸. Для моделей, описанных в Разделе 4.3, которыми мы будем пользоваться и в дальнейшем анализе, это число равно единице. Поэтому, точно так же, как и в случае сценарного дерева, представленного на Рис.1, при построении имити­рующего портфеля для рассматриваемых сценарных деревьев в непрерывном времени можно обойтись лишь требованием на безрисковый денежный поток и требованием на денежный поток, равный цене нефти.

В процессе построения имитирующего портфеля выясняется, что скорректированное на риск распределение вероятностей в каждом данном узле сценарного дерева может быть представлено, так же как и действительное распределение вероятностей, многомерным логнормальным распределением цен на нефть. Такое распределение обычно задаётся значениями математических ожиданий этих переменных и коэффициентов ковариации их логарифмов (которые обычно называются ассоциированными ковариациями). Как отмеча­лось в Разделе 3.6, скорректированные на риск математические ожидания имеют смысл форвардных цен на нефть, вне зависимости от используемой модели ценовой динамики. Тот же аргумент, с помощью которого была продемонстрирована логнормальность скор­ректированного на риск распределения вероятностей, объясняет также, что это распреде­ление характеризуется теми же значениями ассоциированных ковариаций, что и действи­тельное распределение. Продемонстрировать это можно, например, строя бинарное сце­нарное дерево по принципу Рис.1, но покрывая много периодов, постепенно сокращая длительность одного периода до нуля и компенсируя это сокращение увеличением числа периодов (Laughton 1997). Расчёт также может быть выполнен путём обращения напря­мую к формулировке процедуры построения имитирующего актива по Блэку-Шоулзу-Мёртону, как показано в работе Merton (1977). Как отмечалось в Разделе 3.6, в результате получается аналог однопериодного анализа, проведённого в Разделе 3.3, имеющий вид дифференциального уравнения. Решение дифференциального уравнения во времени при соответствующем выборе конечного ограничения и граничных условий эквивалентно процедуре поиска финансовой стратегии продления кредита, описанной в разделе 3.5.

Ключевым аспектом модели ценовой динамики, определяющей структуру скорректи­рованного на риск распределения вероятности, является отсутствие неопределённости при определении факторов дисконтирования. Единственным источником неопределённости в модели служит ценовой прогноз, и именно стохастическая структура ценового прогноза определяет структуру неопределённости цен э.у. активов.

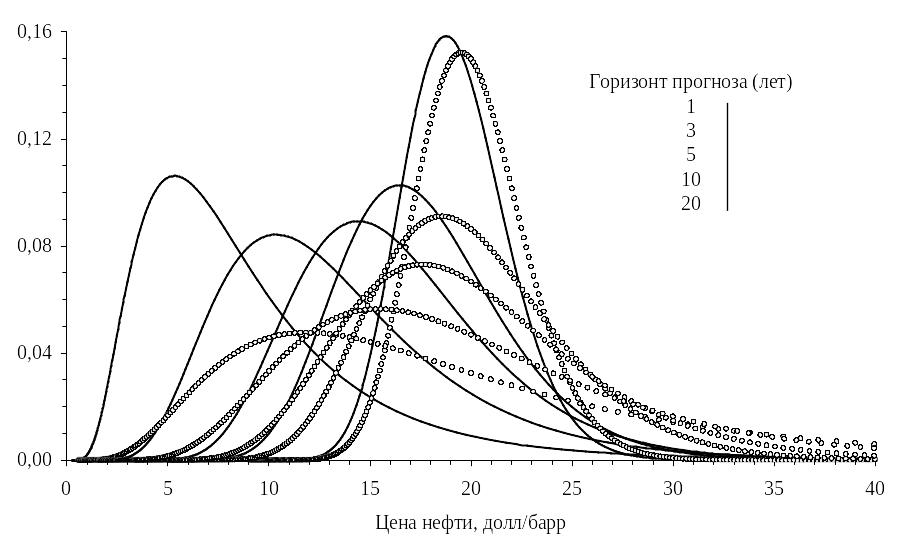
Рис. 5. Действительные (пунктирные линии) и скорректированные на риск (сплошные линии) вероятностные распределения значений цены на нефть. Стохастическая динамика описывается моделью перманентного шока,  = 0,1333 в год.

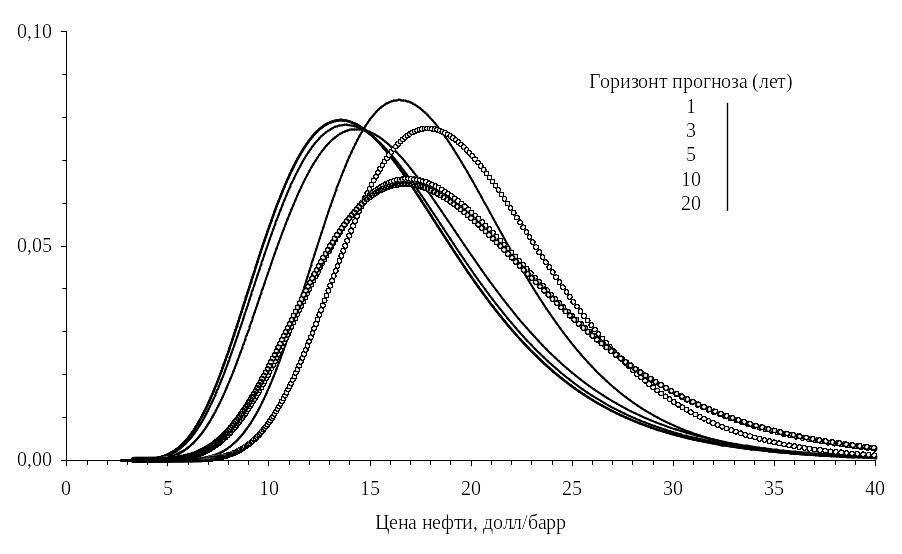
Рис. 6. Действительные (пунктирные линии) и скорректированные на риск (сплошные линии) вероятностные распределения значений цены на нефть. Стохастическая динамика описывается моделью возврата к среднему,  = 0,35 в год.

На Рис. 5 показаны графики одномерных распределений плотности вероятности – дей­ствительных и скорректированных на риск – для прогнозных значений цены на нефть с горизонтом прогноза 1, 3, 5, 10 и 20 лет в случае, когда ценовая динамика описывается моделью перманентного шока с коэффициентом пропорциональной неопределённости 0,133 в годовом выражении. На Рис. 6 показаны аналогичные графики для модели воз­врата к среднему с коэффициентом краткосрочной пропорциональной неопределённости 0,35 в годовом выражении.

Обратите внимание на то, что дисперсия ценовых значений и величина левостороннего сдвига, отражающего поправку на риск, как и следовало ожидать, растут с увеличением прогнозного горизонта. Кроме того, оба эти эффекта в долгосрочной перспективе гораздо ярче выражены в случае модели перманентного шока, чем в случае модели возврата к среднему, причём в последнем случае для них наблюдается существование некоторого предела насыщаемости.