2.3 Подання сигналів в ортогональних базисах

Серед різноманітних математичних прийомів, які використовуються при описі електричних кіл і сигналів, найбільш широко застосовується подання довільної функції у вигляді суми більш простих (“елементарних”) функцій. Нехай s(t) – детермінований сигнал тривалості T_s. Представимо його зваженою сумою деяких базисних функцій

, 0  t  T_s, (2.20)

де a_n – коефіцієнти розкладання,

_n(t) – базисні функції.

Базисні функції вибираються з тих або інших міркувань, потім розраховуються коефіцієнти розкладання. Але найбільш просто коефіцієнти розкладання розраховуються, якщо базисні функції ортогональні на інтервалі (0, Т_s). Помножимо ліву й праву частини рівності (2.20) на _k(t) і проведемо інтегрування на інтервалі (0, Т_s):

.

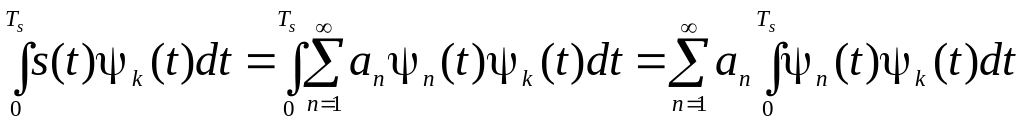Інтеграли в правій частині в силу ортогональності функцій _n(t) і _k(t) дорівнюють нулю крім випадку n = k – у цьому випадку інтеграл дорівнює енергії k-ї базисної функції . Тому остання рівність запишеться

.

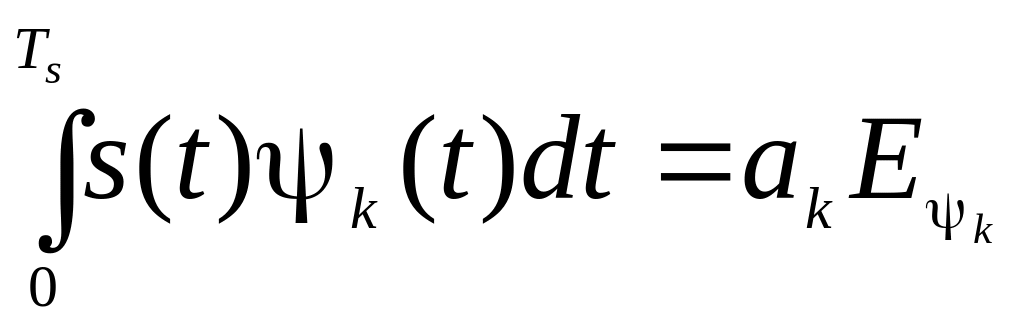Повернемося до індексу n і запишемо правило обчислення коефіцієнтів розкладання

; n = 1, 2, 3, ... (2.21)

Якщо ж базисні функції не тільки ортогональні, а ще й нормовані (ортонормовані), то

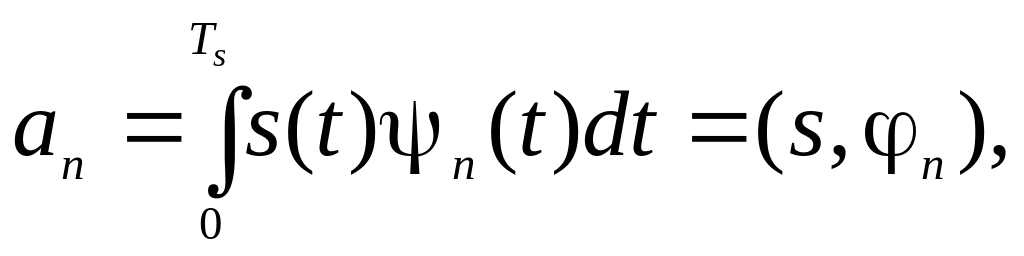n = 1, 2, 3, ... (2.22)

Ряд (2.20), у якому коефіцієнти розкладання визначаються за формулою (2.21), називається узагальненим рядом Фур'є.

При практичному використанні розкладання (2.20) доводиться обмежуватися скінченим числом доданків, що дає наближений сигнал

. (2.23)

При цьому енергія різниці між s(t) і (похибки) визначається

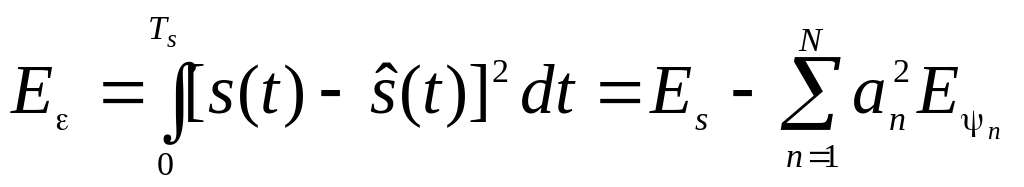. (2.24)

Звичайно вважають, що число N обране так, щоб задовольнити заданій мірі точності, а саме, енергія похибки не перевищує деяке допустиме значення . Тоді в записі розкладання сигналу s(t) використовують знак точної рівності

. (2.25)

Залежно від властивостей сигналу s(t) або задачі, що вирішується, використовують ті чи інші системи базисних ортогональних функцій: тригонометричні функції, експонентні функції, функції відліків, функції Уолша.

Після того, як виконано розкладання сигналу s(t) у ряд, коефіцієнти розкладання повністю задають сигнал s(t), тобто за коефіцієнтами можна відновити сигнал. Коефіцієнти розкладання дозволяють також визначити енергетичні характеристики сигналів: енергію сигналу s(t)

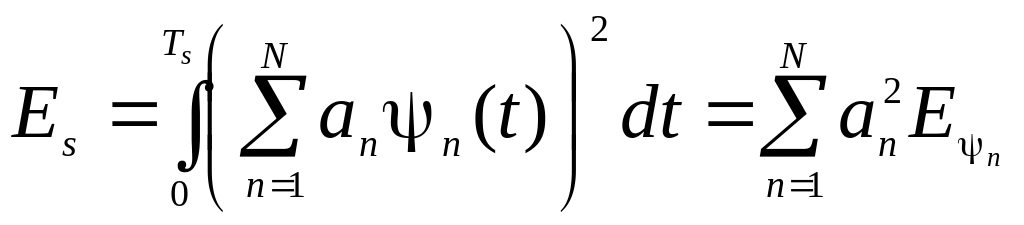(2.26)

і скалярний добуток сигналів s₁(t) і s₂(t)

, (2.27)

де a_n1 і a_n2 – коефіцієнти розкладання сигналів s₁(t) і s₂(t) відповідно.

Визначення коефіцієнтів розкладання можна виконати й апаратно за схемою, наведеною на рис. 2.3, а. Ця процедура називається аналізом сигналу. Знайдені коефіцієнти розкладання повністю описують сигнал. Знаючи їх, можна синтезувати сигнал – відновити його за коефіцієнтами розкладання (рис. 2.3, б). Схеми, наведені на рис. 2.3, знаходять застосування в техніці зв'язку при деяких методах передавання: у передавальному пристрої ведеться аналіз сигналу, каналом зв'язку передаються коефіцієнти розкладання, у прийомному пристрої ведеться синтез сигналу.

2.4 Геометричне подання сигналів

П ри математичному описі сигнали зручно розглядати як такі, що належать деякому N-вимірному простору. Тоді кожний із сигналів відображається вектором або точкою в цьому просторі (рис. 2.4) (точка – це кінець вектора). Згадаємо, що вектор – це відрізок заданого напрямку й довжини. Звичайно вектор задають координатами його кінця. Ясно, що повинна бути задана система координат. Вона задається ортами – векторами одиничної довжини, кути між якими рівні 90. Отже, сигналу s(t) ставиться у відповідність вектор .

Основні співвідношення для N-вимірного лінійного метричного простору:

– довжина (норма) вектора

= , (2.28)

– відстань між векторами й

, (2.29)

– скалярний добуток векторів і

. (2.30)

Функціональним простором називається сукупність всіх функцій часу, заданих на інтервалі (0, T_s). Ці функції розглядаються як вектори у функціональному просторі. Координатами цих векторів є значення самих функцій часу. Ясно, що N  ∞, а співвідношення (2.28)…(2.30) переходять у наступні

– довжина (норма) вектора

, (2.31)

важливо пам'ятати, що довжина вектора дорівнює кореню з енергії сигналу;

– відстань між векторами й

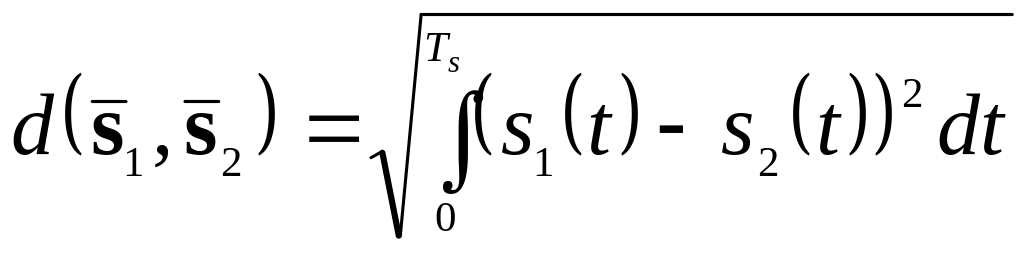; (2.32)

– скалярний добуток векторів і

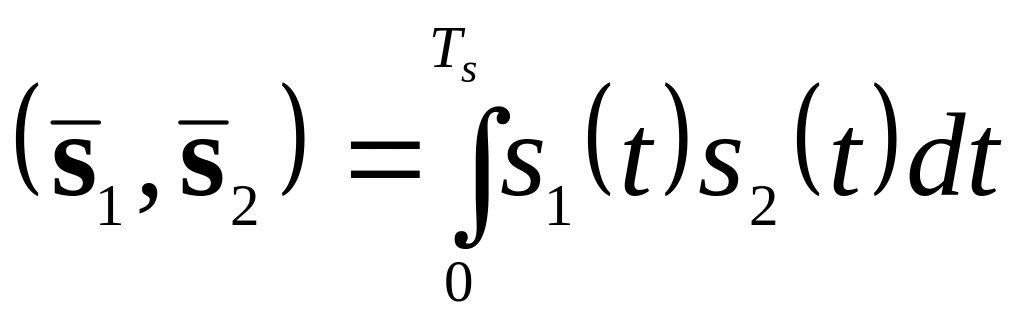. (2.33)

Звернемося до розкладання сигналів в узагальнений ряд Фур'є:

. (2.34)

Уважаємо, що базисні функції ортогональні й нормовані, і їх можна вважати ортами . Перепишемо співвідношення у векторній формі

. (2.35)

Отже, якщо сигнал розкласти в узагальнений ряд Фур'є, то він може бути представлений в N-вимірному просторі.