4.3 Частотна й фазова модуляція

Ці два методи модуляції відносяться до кутових видів модуляції (КМ) – амплітуда модульованого сигналу залишається незмінною, а аргумент (кут) тригонометричної функції-переносника u_пер(t) = a₀ cos(2f₀t + ₀) одержує прирости (t), обумовлені процесом модуляції. Тому сигнал КМ можна записати

u_КМ(t) = a₀ cos(2f₀t + (t) + ₀) = a₀ cos(t). (4.17)

Функцію (t) називають кутом, повною фазою, миттєвою фазою або просто фазою сигналу, а ₀ – початковою фазою сигналу. Миттєва частота сигналу при заданій функції (t) визначається

, (4.18)

де (4.19)

– приріст частоти.

У переносника u_пер(t) миттєва частота f(t) = f₀ – константа, а миттєва фаза лінійно залежить від часу: (t) = 2f₀t + ₀.

При заданій функції f(t) миттєва фаза сигналу визначається

, (4.20)

тобто, приріст фази

. (4.21)

Початкову фазу ₀ можна розглядати як постійну інтегрування.

При фазовій модуляції (ФМ) приріст фази пропорційний миттєвим значенням сигналу, що модулює

(t) = _д b(t), (4.22)

де _д – коефіцієнт пропорційності, що називається девіацією фази. Оскільки максимальне за модулем значення b(t)_max=1, то девіація фази при ФМ це найбільше відхилення фази від лінійної залежності в часі.

Математичний опис сигналу ФМ

s_ФМ(t) = A₀ cos(2f₀ t + _д b(t) + ₀). (4.23)

Під час фазової модуляції миттєва частота залежить від сигналу, що модулює наступним чином

. (4.24)

При частотній модуляції (ЧМ) приріст частоти пропорційний миттєвим значенням сигналу, що модулює

f(t) = f_д b(t), (4.25)

де f_д – коефіцієнт пропорційності, що називається девіацією частоти й визначає максимальне відхиленню миттєвої частоти модульованого сигналу від частоти переносника f₀.

Під час частотної модуляції має місце приріст фази

. (4.26)

Математичний опис сигналу ЧМ одержимо підстановкою виразу (4.26) у формулу (4.17):

. (4.27)

Оскільки b(t) входить у цей вираз під знаком інтегралу, то ЧМ часто називають інтегральним видом модуляції.

З наведених описів сигналів випливає, що ЧМ і ФМ мають багато спільного. Під час модуляції як у випадку ЧМ, так і у випадку ФМ мають місце прирости і частоти, і фази. Назва виду модуляції визначається тим, який з параметрів одержує приріст, пропорційний сигналу, що модулює. Початкова фаза ₀ залежить лише від вибору початку відліку часу, тому її значення не впливає на часові й спектральні характеристики сигналів, які розглядаються. Для спрощення подальших записів приймемо ₀ = 0.

Перепишемо вираз (4.17) у квадратурній формі

u_КМ(t) = a₀ cos(2f₀t + (t)) = a₀ cos(t) cos2f₀t – a₀ sin(t) sin2f₀t. (4.28)

З останнього виразу видно, що сигнал кутової модуляції можна розглядати як суму двох сигналів БМ. Спектр кожного з них визначається зсунутими на частоту f₀ спектрами функцій cos(t) і sin(t), а спектр сигналу u_КМ(t), відповідно до властивості лінійності перетворення Фур'є, їх сумою. Оскільки функції cos(t) і sin(t) нелінійні, то їхні спектри можуть істотно відрізнятися від спектру функції (t) – у спектрах функцій cos(t) і sin(t) можуть з’явитися кратні й комбінаційні частоти, як при нелінійних перетвореннях сигналів, які розглянуть в розділі 3. Отже, при кутових модуляціях зв'язок між спектром сигналу, що модулює, й спектром модульованого сигналу значно складніший, ніж при АМ і її різновидах, тому особливості спектрів сигналів КМ вивчають, приймаючи:

b(t) = cos2Ft (4.29)

– сигнал, що модулює, – гармонічне коливання частоти F.

З врахуванням (4.29) сигнали ФМ і ЧМ запишуться

s_ФМ(t) = A₀ cos(2f₀ t + _д cos2Ft). (4.30)

. (4.31)

На рис. 4.8 наведені часові діаграми сигналу, що модулює, (4.29) і модульованих сигналів (4.30) і (4.31), розраховані при певних числових значеннях, які входять у вирази. На рисунку витримані взаємні часові співвідношення. Легко переконатись, що наведений сигнал ЧМ відповідає сигналу, що модулює: на часовому інтервалі, де миттєві значення сигналу b(t) збільшуються, також збільшуються значення миттєвої частоти сигналу s_ЧМ(t) й навпаки. Саме миттєву частоту легко відслідковувати на часових діаграмах, оскільки період коливань є зворотною величиною до частоти. Під час фазової модуляції приріст частоти відповідно до (4.24) буде пропорційний похідній db(t)/dt, що наведена на рисунку. Бачимо, що значення миттєвої частоти сигналу s_ФМ(t) відповідають значенням функції db(t)/dt.

З рис. 4.8 видно, що при модуляції гармонічним коливанням сигнали ЧМ і ФМ збігаються за формою, вони лише взаємно зсунуті на чверть періоду коливання сигналу, що модулює, а значить їхні амплітудні спектри однакові (властивість перетворення Фур'є – спектр сигналу зсунутого у часі). Для подальшого аналізу спектрів сигналів ЧМ і ФМ уводяться індекси модуляції:

m_ЧМ = f_д /F (4.32)

– індекс частотної модуляції, що визначається відношенням девіації частоти сигналу ЧМ до частоти сигналу, що модулює;

m_ФМ = _д (4.33)

– індекс фазової модуляції, що дорівнює девіації фази сигналу ФМ.

Сигнали ЧМ і ФМ з урахуванням прийнятих позначень записуються у вигляді

s_ЧМ(t) = A₀ cos (2f₀t + m_ЧМ sin 2Ft); (4.34)

s_ФМ(t) = A₀ cos (2f₀t + m_ФМ cos 2Ft). (4.35)

З останніх виразів видно, що індекс модуляції визначає найбільший приріст фази в процесі модуляції. Якщо індекси сигналів ЧМ і ФМ однакові, то однакові їхні амплітудні спектри. Вирази (4.34) і (4.35) підтверджують наведений вище висновок з рис. 4.8, що сигнали ЧМ і ФМ збігаються за формою, вони лише взаємно зсунуті на чверть періоду коливання, що модулює. Для аналізу амплітудних спектрів сигналів ЧМ і ФМ використаємо опис сигналу ЧМ (4.34), позначивши m_ЧМ = m.

За формулою суми косинусів вираз (4.34) перетвориться в

. (4.36)

Функції косинус і синус періодичні в часі, і вони можуть бути представлені рядами Фур’є:

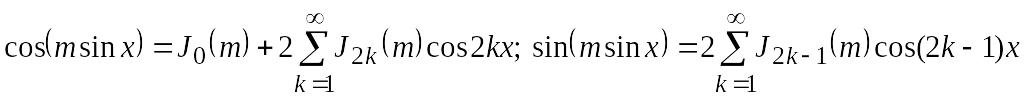, (4.37)

де J_k(m) – функція Бесселя першого роду k-го порядку від аргументу m. Після підстановки (4.37) в (4.36), виконання нескладних перетворень і розкриття добутку тригонометричних функцій, дістанемо

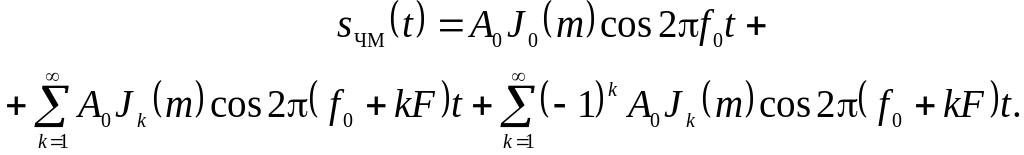(4.38)

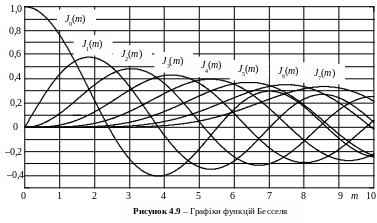
Отже, спектр кутової модуляції при однотональному сигналі, що модулює, такий: перший доданок – гармонічне коливання частоти переносника, перша сума – гармонічні коливання із частотами f₀ + kF (верхня бічна смуга частот), друга сума – гармонічні коливання із частотами f₀ – kF (нижня бічна смуга частот). Кількість складових у верхній і нижній смугах частот теоретично нескінченна, а амплітудний спектр симетричний відносно частоти f₀. Амплітуди спектральних складових визначаються як А₀ J_k(m_ЧМ). Графіки функцій Бесселя для k = 0...7 наведено на рис. 4.9.

Значення функцій Бесселя, яких немає на рис. 4.9, можна розрахувати за рекурентною формулою

. (4.39)

З виразу (4.38) випливає, що протяжність амплітудного спектра нескінченна. Однак основна часка потужності сигналу зосереджена в деякому обмеженому частотному інтервалі навколо f₀, розмір якого і вважають шириною спектра сигналу. Функціям Бесселя властива наступна закономірність: чим більший порядок функції k, тим при більших значеннях аргументу m спостерігаються її істотні значення (рис. 4.9). Для значень k > m + 1 значення функцій Бесселя є малими величинами, тобто, малими будуть амплітуди спектральних складових i ними можна знехтувати. Дійсно, якщо врахувати складові, амплітуди яких не менші за 0,05А₀, то ширина спектра ЧМ і ФМ сигналів розраховується за формулою:

F_ЧМ = F_ФМ = 2F (m + 1). (4.40)

Іноді враховують складові, амплітуди яких не менші за 0,01А₀, і тоді ширина спектра ЧМ і ФМ сигналів розраховується за формулою:

F_ЧМ = F_ФМ = 2F (m + + 1). (4.41)

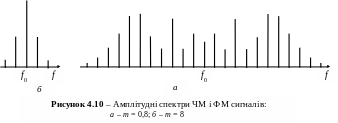
Розрізняють вузькосмугову (у випадку m_ЧМ < 1) і широкосмугову (у випадку m_ЧМ >> 1) модуляції. На рис. 4.10 наведені амплітудні спектри модульованих сигналів з m_ЧМ = 0,8 і m_ЧМ = 8 (частоти складових відрізняються на F). Ширина спектра сигналу вузькосмугової КМ порівнянна із шириною спектра сигналу АМ. Якщо КМ широкосмугова, то у формулі (4.38) можна знехтувати числом 1, і ширина спектра сигналу КМ приблизно дорівнює подвоєній девіації частоти.

Викладений аналіз спектра справедливий як для ЧМ, так і для ФМ. Відмінність між спектрами ЧМ і ФМ сигналів можна виявити, якщо зафіксувати параметри модульованих сигналів і змінювати частоту сигналу, що модулює. У випадку ФМ індекс модуляції m_ФМ залишається незмінним і ширина спектра ФМ сигналу за формулою (4.38) змінюється. У випадку ж ЧМ індекс модуляції m_ЧМ = f_д /F змінюється і ширина спектра ЧМ сигналу за формулою (4.38) практично залишається незмінною.

Якщо сигнал, що модулює, складний, тобто містить ряд гармонічних складових, то спектр ЧМ i ФМ сигналів буде дуже складним, з’являться різні комбінаційні частоти. Як приклад складного (негармонічного) сигналу, що модулює, розглянемо b(t) = А₁ sin 2F₁t + A₂ sin 2F₂t. У цьому випадку модульований сигнал запишеться

s_КМ(t) = А₀cos(2f₀t + m₁sin 2F₁t + m₂sin 2F₂t), (4.42)

де m₁, m₂ – парціальні індекси модуляції (цей вираз описує як сигнал ФМ, так і сигнал ЧМ, якщо цікавитися амплітудним спектром). У спектрі модульованого сигналу будуть такі складові комбінаційних частот

J_k1(m₁) J_k2(m₂) cos(2(f₀  k₁F₁  k₂F₂)t). (4.43)

Кількість складових у порівнянні з випадком модуляції гармонічним коливанням різко збільшується, ускладнюється й аналіз спектра. У випадку складного сигналу, що модулює, з максимальною частотою спектра F_max ширина спектра модульованого сигналу розраховується за формулами

F_ЧМ = 2 (m_ЧМ + 1) F_max, (4.44)

F_ФМ = 2 (m_ФМ + 1) F_max. (4.45)

де m_ЧМ = f_д /F_max. (4.46)