2.11 Дискретизація смугових сигналів

Подання смугових сигналів дискретними необхідно, коли їхнє перетворення (фільтрація, детектування тощо) виконуються процесорами цифрових сигналів. У випадку смугових сигналів, а особливо вузькосмугових сигналів, частота дискретизації може бути істотно менша за 2f_max.

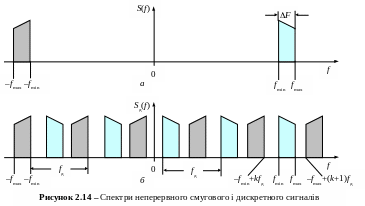
Спектральна густина дискретного сигналу описується виразами (2.63) і (2.63а). На рис. 2.14, а наведено амплітудний спектр довільної форми S(f) смугового сигналу, що зосереджений на інтервалі (f_min, f_max). На рис. 2.14, б зображено амплітудний спектр дискретного сигналу, що може мати місце при дискретизації сигналу зі спектром, наведеним на рис. 2.14, а.

Заради наочності складові спектра дискретного сигналу, які викликані періодичним повторенням смуг частот (f_min, f_max) і (–f_max, f_min), позначені “заливкою” різної густини. Щоб складові спектра на рис. 2.14, б не перекривалися, необхідно так вибрати частоту дискретизації f_д, щоб задовольнити двом умовам, які випливають з рис. 2.14, б:

, (2.86)

де k – ціле число.

Нерівності (2.86) перепишемо так, щоб обмежити знизу і зверху значення частоти дискретизації f_д:

(2.87)

Максимальне значення числа k_max визначається за умови, що складові спектра будуть розміщені максимально близько, з рис. 2.14, б – у формулах (2.86) необхідно знаки нерівностей змінити на знаки рівностей

. (2.88)

За цих рівностей частота дискретизації f_д визначається

. (2.89)

Рішення рівняння (2.89) відносно k_max дає (з урахуванням того, що k ціле)

(2.90)

У випадку, коли k = 0, частота дискретизації f_д  2f_max, тобто це умова вибору частоти дискретизації для первинних сигналів, що задовольняє теоремі Котельникова. Коли k > 0, то подання смугового сигналу дискретним стає більш ощадливим (меншим числом відліків). Найбільш ощадливе подання сигналу буде, коли k = k_max.

Відновлення неперервного смугового сигналу за відліками здійснюється смуговим фільтром, у якого нижня гранична частота смуги пропускання не більша f_min, а верхня гранична частота смуги пропускання не менша f_max.

Контрольні питання до розділу 2

1. Дайте визначення неперервного, дискретного, квантованого і цифрового сигналів.

2. Дайте визначення первинного і вторинного сигналів

3. Дайте визначення детермінованого і випадкового сигналів.

4. Дайте визначення періодичного і неперіодичного сигналів.

5. Дайте визначення простого і складного сигналу.

6. В чому різниця між сигналом та коливанням?

7. Дайте визначення миттєвої потужності сигналу, яка її розмірність і що вона характеризує?

8. Дайте визначення середньої потужності і енергії сигналу.

9. За яких умов сигнал називають нормованим?

10. Дайте визначення кореляційної функції сигналу.

11. Що називають узагальненим рядом Фур'є? Запишіть його вираз та вираз розрахунку коефіцієнтів розкладання.

12. Поясніть поняття аналіз та синтез сигналу.

13. Запишіть основні співвідношення для N-вимірного лінійного метричного простору.

14. Запишіть відомі Вам форми ряду Фур'є при тригонометричному базисі.

15. Дайте визначення амплітудного і фазового спектра періодичного сигналу.

16. Дайте визначення поняттям основна частота і гармоніка сигналу, ширина спектра сигналу.

17. Яким чином здійснюють спектральний аналіз періодичного і неперіодичного сигналів? В чому принципова відмінність їх спектрів?

18. Наведіть відомі Вам властивості перетворення Фур'є.

19. В чому особливість спектра дискретного сигналу? Як здійснюють дискретний спектральний аналіз?

20. Сформулюйте теорему Котельникова та доведіть її в частотній області.

21. Що називається рядом Котельникова і що він ілюструє?

22. Дайте визначення смугового і вузькосмугового сигналів. Як їх описують, які їх основні параметри?

23. Запишіть відомі Вам форми подання смугового сигналу.

24. Який сигнал називається аналітичним і що необхідно для його отримання?

25. Поясніть особливості дискретизації смугових сигналів.