2.8 Теорема й ряд Котельникова

Теорема В.О. Котельникова стверджує: сигнал s(t), який не містить частот вищих F_max, може бути точно відновлений за відліками, узятими через інтервал T_д  1/(2F_max), T_д – інтервал дискретизації, f_д = 1/T_д – частота дискретизації.

Оскільки для будь-якого реального сигналу можна вказати значення максимальної частоти спектра, то можна вважати, що теорема Котельникова може бути застосована до всіх реальних сигналів.

Для доказу теореми розглянемо дискретний сигнал, що описується формулою (2.50) і є послідовністю відліків s(nT_д). Представлення дискретного сигналу за допомогою дельта-функцій можна дати і в іншій формі

. (2.61)

Співвідношення (2.50) і (2.61) еквівалентні, оскільки значення суми дельта-функцій відмінні від нуля тільки в моменти часу t = nT_д.

Спектральна густина добутку сигналів дорівнює згортці спектральних густин співмножників – формула (2.47). Спектральну густину неперервного сигналу позначимо S(j). Оскільки сума дельта-функцій є періодичний сигнал з періодом T_д, то представимо її рядом Фур’є в комплексній формі:

, (2.62)

де 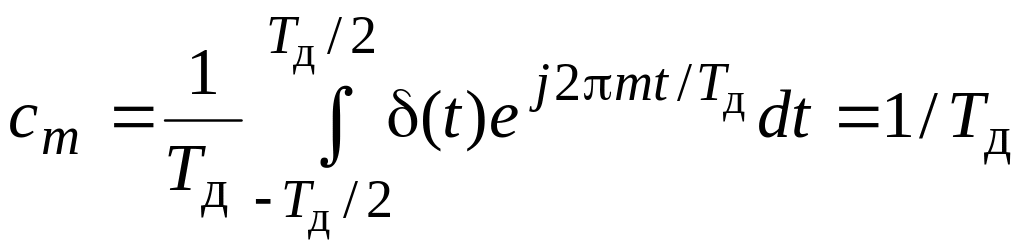. (2.63)

(2.64)

Спектральна густина комплексної експоненти згідно (2.44) дорівнює 2( + 2m/T_д), і спектральна густина суми дельта-функцій (2.64) запишеться

. (2.65)

Знайдемо згортку спектральних густин S(j) і S_(j)

. (2.66)

Змінюючи порядок інтегрування і підсумовування і використовуючи фільтруючу властивість дельта-функції, одержимо

(2.67)

або, переходячи до частоти дискретизації f_д,

. (2.67а)

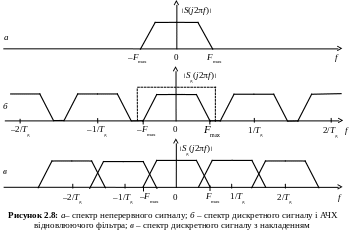
Із (2.67а) видно, що спектральна густина дискретного сигналу є періодичне повторення з періодом f_д спектральної густини неперервного сигналу, з якого отримано дискретний сигнал шляхом узяття відліків. Сказане ілюструється графічно: на рис. 2.8, а показано амплітудний спектр довільного неперервного сигналу з максимальною частотою спектра F_max, на рис. 2.8, б показане його періодичне повторення, що відповідає співвідношенню (2.67) – рисунок побудований для випадку T_д < 1/(2F_max) чи f_д > 2F_max. З рис. 2.8, б видно, що при f_д  2F_max за дискретним сигналом (відліками) за допомогою ФНЧ можна відновити неперервний сигнал (пунктиром показана АЧХ відновлюючого фільтра). При f_д < 2F_max має місце накладення періодичних повторень спектра (рис. 2.8, в), і відновити без похибки неперервний сигнал неможливо. Тим самим теорема Котельникова доведена.

У часовій області зв'язок між неперервним і дискретним сигналами описується рядом Котельникова

, (2.68)

де – частота зрізу відновлюючого ФНЧ.

Значення s(nT_д) є коефіцієнти розкладання сигналу s(t) по відомій з математики системі ортогональних базисних функцій

, n = ..., (–1, 0, 1, 2, ... (2.69)

Графічна ілюстрація ряду Котельникова дана на рис. 2.9.

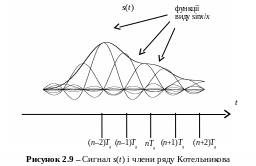
Пояснюється рис. 2.9 наступним чином: при відновленні неперервного сигналу за його відліками ідеальним ФНЧ з частотою зрізу рівною половині частоти дискретизації, відгук фільтра на кожний відлік (δ-функцію) є функцією виду sinx/x з відповідним масштабом і зсувом у часі, сума цих функцій дає сигнал s(t).