
Математические методы обработки экспертной информации - Тинякова В.И
..pdf
- 1 -
Ф е де рал ь н ое аге н т с т во по образован ию РФ В орон е ж с кий гос ударс т ве н н ы й ун иве рс ит е т
В. И . Т иня к о ва
МА Т Е М А Т И Ч Е С К И Е
МЕ Т О Д Ы О БРА БО Т К И
Э К С ПЕ РТ НО Й И НФ О РМ А Ц И И
П О С О Б И Е по специа льно сти080116 (061800)
«М а тема тическ ие мето ды
вэк о но мик е»
СД .Р.09
В орон е ж – 2006
-2 -
Утверж д ен о н а у чн о-м етод ическим советом экон ом ического ф а ку л ь тета ,
протокол № 1 от 12.01. 2006г.
П особие под готовл ен о н а |
ка ф ед ре ин ф орм а цион н ых техн ол огий |
и м а тем а тических м етод ов в |
экон ом ике экон ом ического ф а ку л ь тета |
Ворон еж ского госу д а рствен н ого у н иверситета . Реком ен д у ется д л я сту д ен тов, обу ча ющ ихся по специа л ь н ости 080116 (061800) –«М а те- м а тические м етод ы в экон ом ике», а та кж е д л я сту д ен тов д ру гих специа л ь н остей, прим ен яющ их м етод ы экспертн ого оцен ива н ия при под готовке ку рсовыхи выпу скн ыхква л иф ика цион н ыхра бот.
|
- 3 - |
|
|
О Г Л А В Л Е Н И Е |
|
Пр едисло вие . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
4 |
|
1. С у бъ ек тивные измер ения в эк о но мик е. . . . . . . . . . . . . . . . |
5 |
|
1.1. |
Осн овн ые пон ятия и пробл ем ы теории изм ерен ий. . . . |
5 |
1.2. |
Ш ка л ы изм ерен ий . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
10 |
1.3. |
М етод ы шка л ирова н ия. . . . . . . . . . . . . . . . . . . . . . . . . . . |
16 |
2.М ето ды индивиду а льно го игр у ппо во го
эк спер тно го о ценива ния . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
19 |
|
2.1. |
М етод па рн ыхсра вн ен ий . . . . . . . . . . . . . . . . . . . . . . . . |
19 |
2.2. |
Гру пповое оцен ива н ие с од н оврем ен н ым а н а л изом |
|
|
ком петен тн ости экспертов . . . . . . . . . . . . . . . . . . . . . . . |
22 |
2.3. |
Экспертн ое оцен ива н ие объектов с а втом а тическим |
|
|
отра ж ен ием зн а чим ости ихча стн ыхха ра ктеристик . . |
26 |
3. О ценк а со гла со ва нно стимнений эк спер то в. . . . . . . . . . . . |
28 |
|
3.1. |
Ра н говые коэф ф ициен ты коррел яции . . . . . . . . . . . . . . |
28 |
3.2. |
К оэф ф ициен ты кон корд а ции . . . . . . . . . . . . . . . . . . . . . |
33 |
3.3. |
А н а л изн есогл а сова н н ости м н ен ий экспертов . . . . . . . |
40 |
Т ест. |
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
46 |
А на литическ ие за да ния . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
51 |
|
К о мпью тер ный пр а к тик у м . . . . . . . . . . . . . . . . . . . . . . . . . . |
52 |
|
С писо к литер а ту р ы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
63 |
|
Пр ило ж ение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
64 |
|
- 4 -
П Р Е Д И С Л О В И Е
П рин ято счита ть , что н еобход им ость в экспертн ых оцен ка х возн ика ет ка ж д ый ра з, когд а отсу тству ет тот объем и то ка чество ин ф орма ции, кото-
рые мог л и бы |
га ра н тирова ть |
од н озн а чн ость |
резу л ь та тов |
прин им а емых |
|||||||||
решен ий. Это им еет м есто в тех сл у ча ях, когд а |
н ед оста точн о хорошо изу - |
||||||||||||
чен а вся совоку пн ость обстоятел ь ств |
(л ибо их, |
в |
прин ципе, |
н ел ь зя |
изу - |
||||||||
чить ), в |
которых хозяйству ющ ий су бъект |
вын у ж |
д ен осу щ ествл ять |
свою |
|||||||||
у пра вл ен ческу ю д еятел ь н ость . |
|
|
|
|
|
|
|
|
|
|
|||
П о |
су ти, |
эти |
обстоятел ь ства |
пред ста вл яют |
собой |
своеобра зн ые |
|||||||
проявл ен ия н еопред ел ен н ости. |
С а м а |
ж е |
н еопред ел ен н ость |
м н огол ика , |
|||||||||
имеет |
ра зл ичн у ю |
природ у |
и |
требу ет |
специа л ь н ых |
под ход ов |
д л я |
||||||
преод ол ен ия тех ба рь еров, которые н е позвол яют |
обосн ова ть |
и оцен ить |
|||||||||||
ра цион а л ь н ость прин има ем ых решен ий. Экспертн ое оцен ива н ие ка к ра з и есть од ин изта кихпод ход ов.
Всл ед ствие того, что д а н н ое пособие ориен тирова н о н а техсту д ен тов, которым в бу д у щ ем бу д ет присвоен а ква л иф ика ция «экон омистма тема тик», в н ем особое вн им а н ие у д ел ен о им ен н о ма тем а тическим м е- тод а м , прим ен яемым д л я обобщ ен ия и а н а л иза экспертн ой ин ф орм а ции. В
пособии с д оста точн ой степен ь ю |
д ета л иза ции изл а га ется м етод па рн ых |
|
сра вн ен ий, |
обсу ж д а ются вопросы, |
связа н н ые с оцен кой ком петен тн ости |
экспертов, |
описыва ются процед у ры проверки согл а сова н н ости их мн ен ий, |
|
а та кж е ра ссма трива ется од ин извозмож н ыхва риа н тов а н а л иза причин н е- согл а сова н н ости точек зрен ий экспертов.
Все теоретические выкл а д ки ил л юстриру ются пра ктическим и ра счета м и в MS Excel и STATISTICA, а д л я проверки зн а н ий и за крепл ен ия н а - выков в пособии привед ен о д оста точн о бол ь шое числ о за д а н ий и тестовых вопросов д л я са мостоятел ь н ой ра боты.
В резу л ь та те изу чен ия ма тем а тических метод ов обра ботки экспертн ой
ин ф орма ции сту д ен т д ол ж ен зн а ть |
кл ючевые пол ож ен ия |
теории изм ере- |
н ия и у м еть корректн о осу щ ествл ять |
преобра зова н ие д а н н |
ых в ра зл ичн ых |
шка л а х, гра мотн о обра ба тыва ть резу л ь та ты ин д ивид у а л ь н ого и гру ппового экспертн ого оцен ива н ия, а та кж е провод ить проверку согл а сова н н ости гру пповых экспертн ых оцен ок и а н а л изирова ть причин ы их н есогл а сова н - н ости с испол ь зова н ием соврем ен н ыхпа кетов прикл а д н ыхпрогра м м .

- 5 -
1. С У БЪ Е К Т И В НЫ Е И ЗМ Е РЕ НИ Я В Э К О НО М И К Е
1.1. О сно вные по ня тия ипр о блемы тео р ииизмер ений
И |
н ф орм а ция , ка к |
известн о, явл яется |
од н им |
из свойств м а терии, |
||||||||||||||
опред ел яемым |
через |
м еру |
у м ен ь шен ия |
|
н еопред ел ен н ости |
зн а н ия |
о |
|||||||||||
свершен ии |
ка кого-л ибо |
события |
и |
пон има ем ым |
ка к совоку пн ость |
|||||||||||||
свед ен ий о н екотором объекте. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
П ричем л юба я, в том числ е и экспертн а я, ин ф орма ция имеет цен н ость |
||||||||||||||||||
тол ь ко тогд а , когд а |
ее мож |
н о |
пра вил ь н о |
ин терпретирова ть , |
а |
д л я этого |
||||||||||||
преж |
д е всего н еобход им о корректн о изм ерить пол у чен н у ю ин ф орма цию. |
|||||||||||||||||
И |
з м е ре н ие –это процед у ра , с помощ ь ю которой изм еряемый объект |
|||||||||||||||||
сра вн ива ется с н екоторым эта л он ом и пол у ча ет числ овое выра ж |
ен ие в оп- |
|||||||||||||||||
ред ел ен н ом |
ма сшта бе и шка л е. Ра зра боткой м етод ов и под ход ов, обеспе- |
|||||||||||||||||
чива ющ их объективн ость |
сра вн ен ий в |
ра зл ичн ых ситу а циях, |
за н има ется |
|||||||||||||||
т е ория из м е ре н ий. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ра ссмотрим |
осн овн ые пон ятия теории |
изм ерен ий. |
Д л я |
этого д а д им |
||||||||||||||
опред ел ен ие сл ед у ющ им термин а м : |
объект |
измерен ия, |
пока за тел ь (при- |
|||||||||||||||
зн а к), процед у ры сра вн ен ия. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
О бъе кт а м и из м е ре н ия |
могу т быть |
пред м еты, |
явл ен ия, |
решен ия. |
В |
|||||||||||||
ка честве пока з а т е ле й |
испол ь зу ются |
ха ра ктеристики |
объектов |
ра зл ичн ой |
||||||||||||||
природ ы (простра н ствен н о-врем ен н ые, |
ф изические, |
ф изиол огические, |
||||||||||||||||
психол огические и д р.). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Проце дуры |
сра вн е н ия |
|
вкл юча ют |
опред ел ен н ые |
отн ошен ия м еж |
д у |
||||||||||||
объекта м и |
и |
способ |
сра вн ен ия |
объектов. |
Т а к |
ка к |
|
сра вн ен ие |
||||||||||
кол ичествен н ых д а н н ых |
н е |
вызыва ет |
за тру д н ен ий, |
то |
ра ссмотрим |
|||||||||||||
сра вн ен ие объектов |
н е им еющ их кол ичествен н ого описа н ия. |
С ра вн ен ие |
||||||||||||||||
та ких объектов, |
ка к |
пра вил о, |
н осит |
ка чествен н ый ха ра ктер: |
«бол ь ше», |
|||||||||||||
«м ен ь ше», «ра вн ы», «л у чше», |
«ху ж е», |
«од ин а ковы», |
«пред почтител ь н ее» |
|||||||||||||||
и т.п. С пособсра вн ен ия опред ел яет, |
н а прим ер, сра вн ен ие всех объектов |
|||||||||||||||||
посл ед ова тел ь н о с од н им |
объектом ил и сра вн ен ие всех объектов д ру г с |
|||||||||||||||||
д ру гом в произвол ь н ой посл ед ова тел ь н ости. |
|
|
|
|
|
|
|
|||||||||||
Д л я ф орма л ь н ого описа н ия мн ож |
ества |
объектов и отн ошен ий м еж |
д у |
|||||||||||||||
н им и ввод ится пон ят ие эм пириче ской сист е м ы сот н оше н иям и |
|
|
||||||||||||||||
гд е = { = {
За пись
М = О ; R , |
(1.1) |
1 2 K,, On,} –OмнOож Oество объектов;
1 2 K,, Rm,} –RмнRож Rество отн ошен ий.
O Rозн а ча ет, что объект |
O н а ход ится в отн ошен ии |
R к |
j i k |
i |
k |
объект у Oj . Т а кое отн ошен ие н а зыва ется двум е ст н ым (бин а рн ым ). М огу т быть трехм естн ые отн ошен ия.
- 6 -
Реа л ь н о примен яемые отн ошен ия обычн о обл а д а ют опред ел ен н ым н а бором свойств. В ка честве осн овн ых свойств мож н о н а зва ть сл ед у ю-
щие:
1)отн ошен ие R реф л ексивн о, есл и Oi ROi истин н о;
2) |
отн ошен ие R а н тиреф л ексивн о, есл и Oi ROi л ож н о; |
|
||||||
3) |
отн ошен ие R сим метричн о, есл и из Oi ROj сл ед у ет Oj ROi ; |
|||||||
4) |
отн ошен иеR а н тисимм етричн о, есл и |
из Oi ROj и |
Oj ROi сл ед у ет |
|||||
|
Oi |
= Oj ; |
|
|
|
|
|
|
5) |
отн ошен иеR н есим метричн о (а симм етричн о), есл и |
из истин н ости |
||||||
|
Oi ROj сл ед у ет, что Oj ROi |
л ож н о; |
|
|
||||
6) |
отн ошен иеR тра н зитивн о, |
есл и из |
Oi ROj и Oj ROk сл ед у ет |
|||||
|
O RO , гд е , |
, |
ik |
O ; |
O O |
|
|
|
|
i |
k |
|
j |
|
|
|
|
7) |
отн ошен иеR л ин ейн о (связн о), есл и |
д л я л юбых |
i , j OOл ибOо |
|||||
Oi ROj , л ибо Oj ROi истин н о, л ибо он и оба истин н ы.
В пра ктике провед ен ия ра зл ичн ых иссл ед ова н ий ча сто испол ь зу ются отн ошен ия, обл а д а ющ ие н е всем н а бором свойств, а тол ь ко н екоторым и из выше перечисл ен н ых. П рим ера м и под обн ых отн ошен ий явл яются отн о-
шен ия, опред ел ен ия которыхпривод ятся н иж |
е. |
Отн ошен ие R н а зыва ется от н оше н ие м |
ча ст ичн ого порядка , есл и он о |
реф л ексивн о, а н тисим метричн о и тра н зитивн о. |
|
Отн ошен ие R н а зыва ется от н оше н ие м |
лин е йн ого порядка , есл и он о |
реф л ексивн о, а н тисим метричн о, тра н зитивн о и связн о, т.е. отн ошен ие л и- н ейн ого поряд ка , обл а д а ющ ее свойством связн ости.
И н огд а ра ссма трива ют от н оше н ия ст рого ча ст ичн ого или лин е йн ого порядка , обл а д а ющ ие свойством а н тиреф л ексивн ости, а та кж е от н оше н ия ква з ипоря дка (пред поряд ка , почти поряд ка ), н е обл а д а ющ ие свойством а н тисим метричн ости.
Отн ошен ие R н а зыва ется т оле ра н т н ост ью , есл и он о реф л ексивн о и симм етричн о.
Отн ошен ие R н а зыва ется эквива ле н т н ост ью , есл и он о реф л ексивн о, симм етричн о и тра н зитивн о, т.е. эквива л ен тн ость –это тол ера н тн ость , об-
л а д а ющ а я свойством тра н зитивн ости. |
|
||
|
И н терес вызыва ют возмож н ые способы |
пред ста вл ен ия резу л ь та тов |
|
та ких сра вн ен ий. |
В прин ципе ин ф орма ция оботн ошен иях мож ет быть за - |
||
д а н а |
ра зл ичн ым и |
способа м и. Н а прим ер, мож |
н о перечисл ить объекты, |
прин а д л еж а щ ие отн ошен ию. Н о это н е всегд а |
у д обн о. Бол ее ра спростра- |
||
н ен |
м а т ричн ый способ пре дст а вле н ия ин ф орм а цииоб от н оше н ия х. |
||
|
|
|
- 7 - |
|
|
|
|
|
|
|
|
|
|
|
|||||
С у ть |
за д а н ия отн ошен ия |
|
с помощ ь ю |
та кого способа |
в сл ед у ющ ем . |
||||||||||||||
С троки и стол бцы м а трицы |
|
rij |
|
|
|
отн ошен ия |
|
R соответству ют эл емен та м |
|||||||||||
|
|
|
|
||||||||||||||||
всего мн ож ества объектов, т.е. м а трица |
ква д ра тн а я. И н огд а ма трицу от- |
||||||||||||||||||
н ошен ий обозн а ча ют M (R). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
П у сть |
R –отн ошен ие ча стичн ого ил и л ин ейн ого поряд ка . Т огд а , есл и |
||||||||||||||||||
объект Oi |
пред шеству ет Oj , |
т.е. прин а д л еж |
ит отн ошен ию |
R , то н а пере- |
|||||||||||||||
сечен ии i -й строки и |
j -го стол бца в |
м а трице отн ошен ий ста вится 1, в |
|||||||||||||||||
противн ом сл у ча е –0. |
|
|
е сли ( |
|
, |
|
|
|
) R O 1,O |
|
|||||||||
|
|
ì |
|
i |
|
|
j |
|
|||||||||||
|
rij |
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(1.2) |
||
|
= í |
|
е сли ( |
|
|
, |
|
|
|||||||||||
|
|
ï |
|
|
i |
j |
|
)Ï R O0,O |
|
||||||||||
|
|
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
А н а л огичн о, с помощ ь ю м а трицы |
|
rij |
|
|
|
, мож н о за д а ть ин ф орма цию об |
|||||||||||||
|
|
|
|||||||||||||||||
отн ошен ияхтол ера н тн ости ил и эквива л ен тн ости. |
|
||||||||||||||||||
Ра ссмотрим пример м а тричн ого за д а н ия |
отн ошен ия |
ча стичн ого по- |
|||||||||||||||||
ряд ка . С этой цел ь ю эл емен ты м а трицы, за д а ющ ей это отн ошен ие, бу д ем опред ел ять в соответствии с пра вил ом
ì |
е сли |
ï |
е сли |
rij = í |
|
ï |
е сли |
î |
( |
)Î ( |
, |
i |
)Ï,R O , O R O 1O, |
||
( |
)Ï ( |
|
j |
i |
j |
|
, |
i |
)Ï,R . |
O , O (1.3)R O 0O, |
|||
|
|
|
j |
i |
j |
|
|
( |
,- i )Î,jR 1 ) Oi , Oj(Ï R O O |
||||
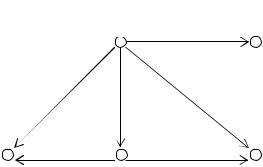
П у сть д л я 5 объектов за д а н о отн ошен ие ча стичн ого поряд ка . Гра ф , ил л юстриру ющ ий это отн ошен ие, изобра ж ен н а рис. 1.1.
О 1
О 3
О 4 |
|
О 2 |
О 5 |
Ри с. 1.1. Гра ф , ил л юстриру ющ ий отн ошен ие ча стичн ого поряд ка
Ма трица , сод ерж а щ а я ин ф орма цию оботн ошен ии ча стичн ого поряд ка R , в ра ссм а трива емом сл у ча е им еет вид

|
|
- 8 - |
|
|
|
|
|
|
æ |
|
|
1 |
1 |
ö |
10 |
1 |
|
ç |
- |
|
|
1 |
÷ |
1 |
01 |
0 |
ç |
|
|
÷ |
|||||
M(R) = ç |
- |
|
|
00 |
÷ |
.0 1 0 |
||
ç |
- |
- |
0 |
0 |
÷ |
|
01 |
1 |
ç |
÷ |
|
||||||
ç |
- |
- |
0 |
0 |
÷ |
|
01 |
1 |
è |
ø |
|
||||||
А н а л огичн о д л я л ин ейн ого |
поряд ка |
эл емен ты |
ма трицы за д а ются в |
|||||
соответствии со сл ед у ющ им пра вил ом :
ì |
е сли |
ï |
е сли |
rij = í |
|
ï |
е сли |
î |
( |
)Î ( |
, |
|
i |
)Ï,R O , O R O1, O |
||
( |
)Î ( |
|
|
j |
i |
j |
|
, |
i |
)Î,R . |
O , O (1.4)R O0, O |
||||
|
|
|
|
j |
i |
j |
|
|
( |
|
,- i )Î,jR 1 ) Oi , Oj(Ï R O O |
||||
П од обн ые пра вил а без тру д а м ож н о за писа ть д л я л юбого д ру гого от-
ношен ия.
Дл я того чтобы пон ять , у ста н а вл ива ет ил и н ет эмпирическа я систем а с
отн ошен иям и |
н екоторый |
поряд ок м еж |
д у |
сра вн ива емым и |
объекта м и, |
|||
н еобход им о сра вн ить пол у чен н ый поряд ок с числ овой систем ой. |
С этой |
|||||||
цел ь ю н а ша |
привычн а я |
числ ова я |
систем а |
пред ста вл яется |
н екой |
|||
у н иверса л ь н ой системой с отн ошен иям и вид а |
|
|
|
|
||||
|
|
= H; S ,N |
|
|
|
(1.5) |
||
гд е N –мн ож |
ество д ействител ь н ыхчисел ; |
|
|
|
|
|
||
= ( 1 |
2 K,, Sm,) –SSмн ожS ество отн ошен ий меж д у |
числ а м и («бол ь - |
||||||
ше», «мен ь ше», «ра вн о»и т.д .). |
|
|
N есть |
|
|
|
||
Ч исл ова я |
систем а н а зыва ется полн ой, |
есл и |
мн ож |
ество всех |
||||
действител ь н ыхчисел .
Сра вн ен ие эмпирической систем ы с отн ошен ием и числ овой систем ы позвол яют осу щ ествить «оциф ровку »су бъективн ых измерен ий. Н иж е ра с- см а трива ются пробл ем ы, возн ика ющ ие при тра н сф орм а ции су бъективн ых изм ерен ий в кол ичествен н ые.
К ол ичествен н ые д а н н ые, у ж е явл яясь эл ем ен та м и числ овой систем ы, н е требу ют специа л ь н ых процед у рсвоего числ ового пред ста вл ен ия. П робл ем ы возн ика ют при обра ботке н ечисл овой ин ф орма ции. Ч а щ е д ру гих д л я ее пол у чен ия испол ь зу ются экспертн ые м етод ы. У сл овим ся, что д а н - н ые, пол у чен н ые экспертн ым пу тем , явл яются резу л ь та том су бъективн ых изм ерен ий.
Осн овн ые пробл емы су бъективн ых измерен ий –пробл емы пред ста в- л ен ия и ед ин ствен н ости.
Пробле м а пре дст а вле н ия за кл юча ется в д ока за тел ь стве того, что д л я эмпирической системы с отн ошен иями, выбра н н ой с цел ь ю изм ерен ия оп-

- 9 -
ред ел ен н ых свойств объектов, м ож н о построить числ ову ю систем у с от- н ошен иям и, описыва ющ у ю свойства объектов и отн ошен ий м еж д у н им и с
помощ ь ю чисел . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Д л я |
того чтобы числ ова я |
систем а |
сохра н ял а свойства и |
отн ошен ия |
||||||||||||
объектов, н еобход им о, |
чтобы он а был а изоморф н ой ил и, |
по кра йн ей мере, |
||||||||||||||||
гомом орф н ой эмпирической систем е. |
|
|
|
= |
|
2 K, RkM, |
,Rи0;R |
|||||||||||
|
|
Д ве |
|
систем ы |
с |
отн ошен иям и |
1 |
|||||||||||
|
|
= |
1 |
|
2 K, Sm,; |
н,аSHзываS ютсяN |
подобн ым и, |
есл и числ о |
отн ошен ий |
|||||||||
од ин а ково (k = m) и местн ость отн ошен ий од ин а кова (н а прим ер, |
Ri и Si – |
|||||||||||||||||
д ву м естн ые отн ошен ия). |
|
= |
|
|
2 K, RkM, |
из,Rом0орф;R н а |
|
|
||||||||||
|
|
Эмпирическа я систем а |
= |
|
1 |
числ овой |
||||||||||||
систем е с отн ошен иям и |
1 |
|
2 K, Sm,; , |
есл,SHи SэтиNсистем ы под об- |
||||||||||||||
н ы и су щ еству ет вза имн оод н озн а чн ое отобра ж ен ие (ф у н кция) |
f |
объектов |
||||||||||||||||
н а |
|
числ овое мн ож |
ество та кое, |
что отн ошен ие Rk |
м еж д у |
объекта м и им еет |
||||||||||||
место тогд а |
и тол ь ко тогд а , когд а имеет м есто отн ошен ие Sk |
м еж д у |
чис- |
|||||||||||||||
л а м и, явл яющ им ися отобра ж ен ием объектов н а числ ову ю ось . |
(Н а пример, |
|||||||||||||||||
д л я д ву м естн ыхотн ошен ий |
|
OO Oимеет место тогд а и тол ь ко тогд а , ко- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
ji |
|
k |
|
|
|
|
|
|
|
гд а |
им еет м есто |
rr,Sгд е числ а r , |
r |
j |
пол у чен ы отобра ж ен ием объектов |
|||||||||||||
|
|
|
|
|
|
ji |
k |
|
i |
|
|
|
|
|
|
|
|
|
i |
= r (Of), |
j |
=r |
(Of ). |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
i |
|
j |
|
|
|
|
|
|
|
f явл яется в ряд е сл у - |
||||||
|
|
У сл овие вза имн ой од н озн а чн ости отобра ж ен ия |
||||||||||||||||
ча ев сл ишком ж |
естким и н е всегд а н еобход имым . Е сл и у стра н ить это у сл о- |
|
вие изпред ыд у щ его опред ел ен ия, то приход им к пон ятию гом |
ом орф из м а . |
|
Пробле м а |
е дин ст ве н н ост и за кл юча ется в опред ел ен ии |
всех возмож - |
н ых способов пред ста вл ен ия за д а н н ой эм пирической системы ра зл ичн ыми
числ овыми систем а ми. Эта |
пробл ем а |
мож |
ет быть сф орму л ирова н а ка к |
|
пробл ема опред ел ен ия типа шка л . |
|
|
|
|
Ш ка лой н а зыва ется совоку пн ость |
эм пирической системы, числ овой |
|||
системы и отобра ж ен ия, т.е. |
, |
, fM . H |
|
|
Обобщ а я вышеска за н н ое, мож |
н о д а ть |
сл ед у ющ ее опред ел ен ие пон я- |
||
тию «измерен ие». И з м е ре н ие |
–процесс, в ход е которого ха ра ктеристики |
|||
объекта измерен ия пол у ча ют пред ста вл ен ие (гом ом орф н ое отобра ж ен ие) в н екоторой шка л е изм ерен ий.
П у сть  , , fM иH
, , fM иH , , Mg
, , Mg –Hд ве шка л ы с ра зн ыми отобра ж ен иями. Возн ика ет вопрос о вза имосвязи числ овых зн а чен ий, пол у чен н ыхс испол ь зова н ием отобра ж ен ий f и g . Н а прим ер, есл и j =r (Ofj ),
–Hд ве шка л ы с ра зн ыми отобра ж ен иями. Возн ика ет вопрос о вза имосвязи числ овых зн а чен ий, пол у чен н ыхс испол ь зова н ием отобра ж ен ий f и g . Н а прим ер, есл и j =r (Ofj ),
- 10 -
′ =r |
(Og) и связь меж д у |
числ а м и за д а ется ф у н кцией ϕ , т.е. |
r |
j |
= ϕ (r′ ) |
|||
j |
|
j |
|
|
|
|
j |
|
ил и |
( |
j |
)= ϕ [ (Og)], то фfу нOкцию ϕ н а зыва ют допуст им ым |
пре обра з о- |
||||
|
|
j |
|
|
|
|
|
|
ва н ие м |
|
шка лы. С войства |
ф у н кции ϕ опред ел яют |
связи меж д у |
всем и чи- |
|||
сл овым и |
система м и, выбра н н ым и д л я описа н ия |
эмпирической систем ы. |
||||||
Бол ее того, в за висимости от свойств ф у н кции ϕ опред ел яется тип шка л ы,
что позвол яет в н иж есл ед у ющ ем па ра гра ф е провести кл а ссиф ика цию шка л изм ерен ия.
1.2.Ш к а лы измер ений
Извсего мн ож ества теоретически возмож н ыхшка л д л я пол у чен ия экс-
пертн ой ин ф орм а ции в кол ичествен н ом вид е ча щ е всего испол ь зу ются сл е- д у ющ ие типы шка л : н омин а л ь н а я, поряд кова я, ин терва л ь н а я, шка л ы отн о- шен ий и ра зн остей, а бсол ютн а я.
К а ж д а я изэтихшка л опред ел яется н а л ичием ил и отсу тствием четырех ха ра ктеристик: 1) описа н ие; 2) поряд ок; 3) ра сстоян ие; 4) н а ча л ь н а я точка .
О писа н ие шка лы пред пол а га ет испол ь зова н ие ед ин ого способа за писи ин ф орма ции, т.е. ха ра ктеризу ет соста вл яющ ие шка л у эл ем ен ты, н а пример, степен ь у д овл етворен н ости («пол н ость ю у д овл етворен », «в общ ем у д овл е- творен », «скорее н е у д овл етворен », «совсем н е у д овл етворен ») ил и сем ей- н ое пол ож ен ие («состою в бра ке», «н е состою в бра ке»). П ри этом м еж д у д а н н ым и эл емен та м и н е ввод ится ка ка я-л ибо ха ра ктеристика сра вн ен ий, а
осу щ ествл яется тол ь ко ид ен тиф ика ция ин ф орм а ции. |
|
|
|
|
|
|
||||||||||
Порядок |
ха ра ктеризу ет |
н а л ичие |
|
отн ошен ий |
в |
способа х |
за писи |
|||||||||
ин ф орм а ции, |
н а л ичия |
кра йн их точек |
зрен ия |
(«очен ь |
н ра вится», |
|||||||||||
«н ра вится», |
«н е н ра вится», |
«очен ь |
н е |
н ра вится»). |
П ри |
этом |
||||||||||
пред у см а трива ются |
н екоторые |
сра вн ител ь н ые |
ха ра ктеристики, |
|||||||||||||
позвол яющ ие, |
|
н а пример, |
у поряд очить |
отн ошен ие |
к |
пред мет у |
||||||||||
иссл Раед овасстноиян.ие шка лы –изм еряема я вел ичин а . Это озн а ча ет, |
что он о су - |
|||||||||||||||
щ еству ет |
тол ь ко в тех сл у ча ях, |
когд а |
ин ф орм а ция опред ел ен а кол ичест- |
|||||||||||||
вен н о, а |
меж д у |
описа н ием ин ф орма ции |
им еются ин терва л ы, |
ра сстоян ие |
||||||||||||
меж д у которым и имеет см ысл овое зн а чен ие. |
|
|
|
|
|
|
|
|
||||||||
На ча льн а я |
т очка |
за д а ет |
у ровен ь |
соотн ошен ий |
меж |
д у |
эл ем ен та м и |
|||||||||
шка л ы. С л ед у ет |
ра зл ича ть н а ча л ь н у ю точку |
и точку |
отсчета . К а ж |
д а я |
н а - |
|||||||||||
ча л ь н а я точка |
явл яется точкой отсчета , н о н е ка ж |
д а я точка |
отсчета |
мож |
ет |
|||||||||||
быть н а ча л ь н ой. Ш ка л а |
имеет |
н а ча л ь н у ю точку , есл и он а |
им еет ед ин ст- |
|||||||||||||
вен н ое н а ча л о отсчета . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
П ривед ем кра ткое описа н ие всех типов шка л , испол ь зу ем ых в ма рке- |
||||||||||||||||
тин говых иссл ед ова н иях и позвол яющ их резу л ь та ты |
л юбых измерен ий |
|||||||||||||||
пред ста вл ять в кол ичествен н ом вид е. |
|
|
|
|
|
|
|
|
|
|
||||||
