
Курс теории активных систем - Новиков Д.А., Петраков С.Н
..pdf
Механизмы стимулирования в активных системах с вероятностной неопределенностью
представима в таком виде, называется системой с простым активным элементом.
В настоящем разделе будем считать выполненными предположения А.5, А.6 и
А.8. A = A = [0, A+ ] , |
A+ < +¥ . |
|
|
||||
0 |
"z < A+ |
|
|
|
|
|
|
А.9. F(0) = 0 , |
F(z) < 1 . |
|
|
||||
Теорема 3.5. |
В классе M |
|
|
оптимальна следующая функция |
|||
штрафов K - типа: |
|
|
|
|
|
|
|
|
|
ìC, z £ z2 ; |
|
|
|||
|
~ |
ï~ |
~ |
, z3 |
]; |
||
|
χ K (z) = |
íh (z) - h (z3 ), z Î[z2 |
|||||
|
|
ï0, z ³ z |
3 |
, |
|
|
|
|
|
î |
|
|
|
|
|
|
|
~ |
|
|
|
|
~ |
|
|
~ |
|
|
|
|
|
|
|
где z2 = arg max h (z) , |
z3 = max{z ³ z2 | h (z) ³ h (z2 ) - C} . |
|
|
|
|
|
|||||||||||
|
z A0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. Целевая функция АЭ равна математическому |
|||||||||||||||||
ожиданию функции полезности: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
A+ |
~ |
|
|
~ |
|
|
|
|
y |
~ |
|
|
|
|
|
|
f ( y) = ò |
f (z) p(z, y)dz = |
f ( y)[1 - F( y)]+ |
ò |
f (z) p(z)dz , |
|
|
||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
где p(z) |
- соответствующая интегральной функции F(z) плотность |
||||||||||||||||
распределения. Производная целевой функции имеет вид: |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶f ( y) = ¶f ( y) [1 - F( y)]. |
|
|
|
|
|
|
|
||||||
|
|
|
|
¶y |
|
¶y |
|
|
|
|
|
|
|
|
|
|
|
Из приведенного выражения следует, что для простого АЭ отрезки |
|||||||||||||||||
монотонности функции полезности и целевой функции совпадают. |
|
||||||||||||||||
При использовании функции штрафов |
|
~ |
|
~ |
возрастает на |
||||||||||||
χK (z) , f (z) |
|||||||||||||||||
интервале |
[0, z2 ) , постоянна |
на |
интервале |
[z2 , z3 ] , |
|
|
убывает |
на |
|||||||||
интервале |
[z3, + ¥) . |
Аналогично |
ведет |
себя |
|
f ( y) , |
значит z3 - |
||||||||||
реализуемое действие. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Покажем, что для любой допустимой функции штрафов |
|||||||||||||||||
глобальный |
максимум функции |
f ( y) |
|
достигается |
|
при |
y £ z3 . |
||||||||||
Предположим |
противное, |
то |
есть, |
что |
существует |
|
|
глобальный |
|||||||||
максимум |
функции |
f ( y) |
в |
точке |
|
~ |
> z3 |
, |
~ |
|
+ |
, |
то |
есть |
|||
|
y |
y < A |
|
||||||||||||||
"y Î A |
~ |
|
|
При |
этом из детерминированной |
|
теории |
(см. |
|||||||||
f ( y) ³ f ( y) . |
|
||||||||||||||||
теорему 2.1) |
следует, |
что |
глобальный |
максимум функции |
~ |
не |
|||||||||||
f (z) |
|||||||||||||||||
61

ГЛАВА 3
может достигаться при |
z > z3 . То есть, |
найдется точка y′ |
~ |
A |
+ |
||||||||
≤ z3 < y < |
|
||||||||||||
такая, что |
~ |
~ ~ |
~ |
|
|
|
|
|
~ |
|
|
|
|
f (z′ = y′) > f (z |
= y) и при этом |
|
f ( y¢) £ f (y) . |
|
|
|
|||||||
Из связи функций |
f |
~ |
следует неравенство: |
|
|
|
|||||||
и f |
|
|
|
||||||||||
~ ~ |
~ |
~ |
|
|
~ |
|
|
|
|
y′ ~ |
|
|
|
y ~ |
|
|
¢ |
|
|
¢ |
|
|
|
||||
f ( y)[1 - F( y)]+ ò f (z) p(z)dz - f ( y )[1 - F( y )]- ò f (z) p(z)dz ³ 0 , |
|
|
|||||||||||
|
|
0 |
|
|
|
|
~ |
|
|
0 |
|
|
|
~ ~ |
~ |
~ |
|
|
|
~ |
|
|
|
|
|||
¢ |
|
¢ |
y |
|
|
|
|
||||||
откуда: f ( y)[1 - F( y)]+ f ( y )[1 |
- F( y )]+ ò f (z) p(z)dz ³ 0 . |
|
|
|
|||||||||
|
|
|
|
|
|
|
y′ |
|
|
|
|
|
|
Из того, что |
y¢ < |
~ |
~ |
|
|
~ |
~ |
~ |
получим следующую |
||||
y и f (z′ = y′) > |
f (z |
= y) , |
|||||||||||
оценку: |
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
~ ~ |
|
~ |
~ |
|
|
|
|
|
|
|
|
|
|
|
¢ |
|
¢ |
|
y ~ |
|
|
|
|
|||
|
f ( y)[1 - F( y)]- f ( y )[1 - F( y )]+ ò f (z) p(z)dz £ |
|
|
||||||||||
|
~ ~ |
|
|
|
|
|
|
|
y′ |
|
|
|
|
≤ |
~ |
|
~ |
|
|
|
~ |
~ |
|
|
|
||
f ( y)[1− |
F( y)]− |
f ( y′)[1− F( y′)]+ |
f ( y′)[F( y) − F( y′)]= |
|
|
||||||||
~ ~ |
~ |
~ |
|
~ |
|
~ |
|
~ |
~ |
~ |
~ |
|
|
= f ( y)[1− F( y)]− f ( y′) + f ( y′)F( y) |
= [f ( y) − |
f ( y′)][1− F( y)]< 0 , |
|
|
|||||||||
~ |
¢ |
|
|
|
|
|
так как f ( y) < |
f (y ) , а в силу предположения А.9 при |
|||||
Таким образом: |
~ |
|
|
y′ |
||
~ ~ |
~ |
~ |
|
|||
y |
~ |
¢ |
||||
0 > f ( y)[1- F( y)]+ ò |
|
|
¢ |
|||
f (z) p(z)dz - f ( y )[1 |
- F( y )]- ò |
|||||
|
|
0 |
|
|
|
0 |
z < A+ F(z) < 1 .
~ ³
f (z) p(z)dz 0 .
Получили противоречие, значит, не существует глобального максимума функции f ( y) при y > z3 . ·
Итак, в модели простого активного элемента оптимальны компенсаторные системы стимулирования. В то же время, в работе [19] доказано, что в этом классе активных систем скачкообразные системы стимулирования не оптимальны. Задача поиска общих условий (достаточных и, тем более, необходимых) оптимальности различных
систем стимулирования в вероятностных активных системах на сегодняшний день остается открытой.
62

Механизмы стимулирования в активных системах с нечеткой неопределенностью
Глава 4. МЕХАНИЗМЫ СТИМУЛИРОВАНИЯ В АКТИВНЫХ СИСТЕМАХ С НЕЧЕТКОЙ НЕОПРЕДЕЛЕННОСТЬЮ
4.1. Нечеткие множества и отношения1
Нечеткие множества. Пусть X - некоторое множество. Нечетким
подмножеством |
~ |
множества X называется |
множество пар |
|
A |
||||
~ |
(x), x}, |
где |
x X , μ A (x) [0,1] . Функция |
μ A : X → [0, 1] |
A = {μA |
||||
~ |
|
|
~ |
~ |
~
называется функцией принадлежности нечеткого множества A , а X - базовым множеством. Далее в этой главе нечеткие множества обозначаются тильдой.
~ |
|
|
X , |
Носителем множества A называется подмножество множества |
|||
содержащее те элементы из X , для которых значения функции |
|||
~ |
|
μA (x) > 0} . |
|
|
|
||
принадлежности больше нуля: supp A = {x X |
|
|
|
|
|
~ |
|
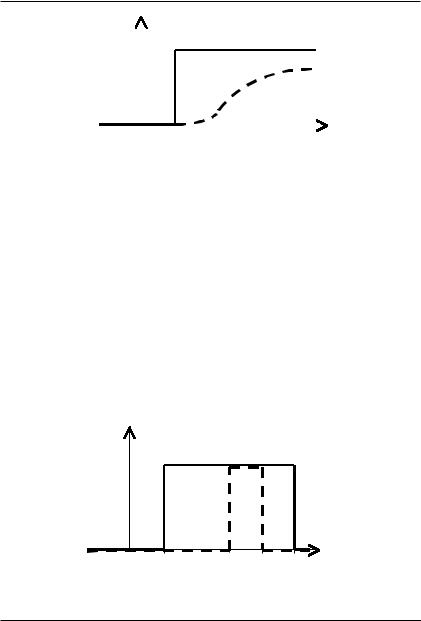
Пример 4.1.2 В качестве примера нечеткого множества рассмотрим нечеткое множество действительных чисел много больших единицы:
~ |
которое |
может |
задаваться |
функцией |
A = {x R1 x >> 1} , |
принадлежности, эскиз которой изображен на рисунке 4.1. Для
сравнения приведем эскиз функции принадлежности четкого множества чисел, строго больших единицы: B = {x R1 x > 1} . ∙
Свойства нечетких множеств.
~
1. Нечеткое множество A называется нормальным, если
sup μ ~ (x) = 1 .
x X
A
1Первые два параграфа данной главы не имеют непосредственного отношения к задачам управления активными системами и содержат необходимые для последующего изложения сведения из теории нечетких множеств [21].
2Приводимые в настоящем разделе примеры иллюстрируют соответствие между четкими и нечеткими множествами.
63
ГЛАВА 4
|
|
1 |
|
|
|
|
|
μ B ( x ) |
|
|||
|
|
|
|
|
|
|
|
|
μ A ( x ) |
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
~ |
|
|
||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
10 |
|
|
|
|
|
|
|
|
Рис. 4.1. Пример четкого |
|
||||||
|
|
|
|
|
и нечеткого множества |
|
||||||
2. Два |
нечетких множества |
~ |
~ |
|||||||||
равны (записывается A |
= B ), если |
|||||||||||
x X , μA |
(x) = μB |
(x) . |
|
|
|
|
|
|||||
~ |
~ |
|
|
|
|
|
|
|
|
|
|
|
Пример 4.2. Задавая четкие множества в виде функций принадлежности, можно сказать, что множества равны, если равны их
функции принадлежности. · |
~ |
|
|
|
|
~ |
|
3. Нечеткое множество |
содержится в нечетком множестве |
||||||
B |
A |
||||||
|
|
~ |
~ |
~ |
x X |
||
или является подмножеством A |
(т.е. B |
Í A ), если |
|||||
μ~ (x) £ μ ~ (x) .
B A
Пример |
4.3. |
Функции |
принадлежности четких подмножеств |
|||
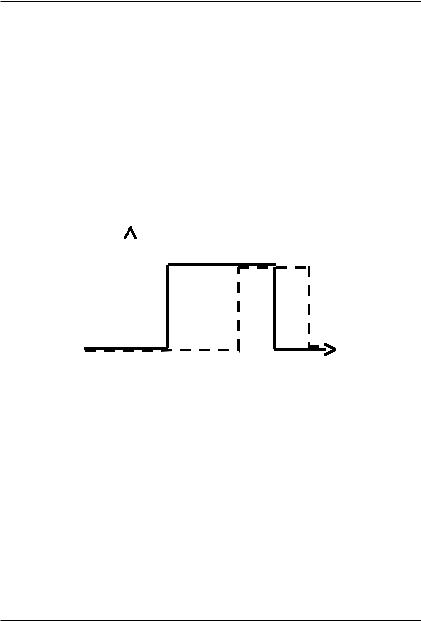
A = [1, 5] и |
B = [3, 4] множества действительных чисел (см. рисунок |
|||||
4.2) имеют вид: μ A |
|
|
ì1, x Î[1, 5]; |
ì1, x Î[3, 4]; |
||
(x) = í |
Ï[1, 5], |
и μB (x) = í |
||||
|
|
|
|
î0, x |
î0, x Ï[3, 4]. |
|
|
|
1 |
|
μ A (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
μB (x)
x
1 |
3 |
4 |
5 |
Рис. 4.2. Включение нечетких множеств
64
Механизмы стимулирования в активных системах с нечеткой неопределенностью
Пользуясь приведенным выше определением принадлежности
множеств, получаем |
B A . Таким |
образом, |
для |
четких |
множеств |
||
определение принадлежности приобретает стандартный вид. ∙ |
|||||||
|
|
~ |
~ |
~ |
~ |
|
называется |
4. Пересечением нечетких множеств A и |
B ( A I B ) |
||||||
наибольшее нечеткое множество, содержащееся как в |
~ |
|
~ |
||||
A , |
так и в B , с |
||||||
функцией принадлежности |
|
|
|
|
|
|
|
μAIB |
(x) = min {μA (x), μB (x)}, x X . |
|
|
|
|||
~ ~ |
~ |
~ |
|
|
|
|
|
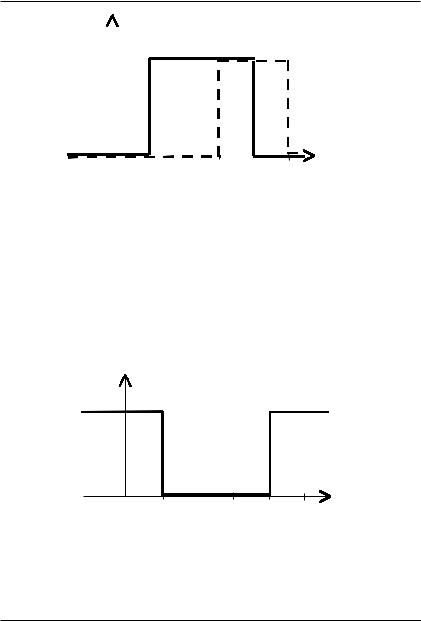
Пример 4.4. Рассмотрим четкие множества |
A = [1, 4] |
и |
B = [3, 5] . |
||||
Пользуясь приведенным выше определением пересечения, получаем,
что для четких множеств определение операции пересечения приобретает стандартный вид (см. рисунок 4.3). ∙
1 |
|
|
μ A (x) |
|
μAIB (x) |
|
|
|
|||
|
|
|
|
|
|
|
|
|
μB (x) |
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
5 |
|
||
|
|
1 |
4 |
|
|||||||
|
|
|
|
|
|
|
|||||
Рис. 4.3. Пересечение множеств |
|
|
|
||||||||
5. Объединением нечетких
наименьшее нечеткое множество,
функцией принадлежности
μ ~ ~ (x) = max{μ ~
AUB A
множеств |
~ |
и |
|
~ |
|
A |
~ |
B |
|||
содержащее |
как |
, |
|||
A |
|||||
(x), μ ~ (x)} , x X .
B
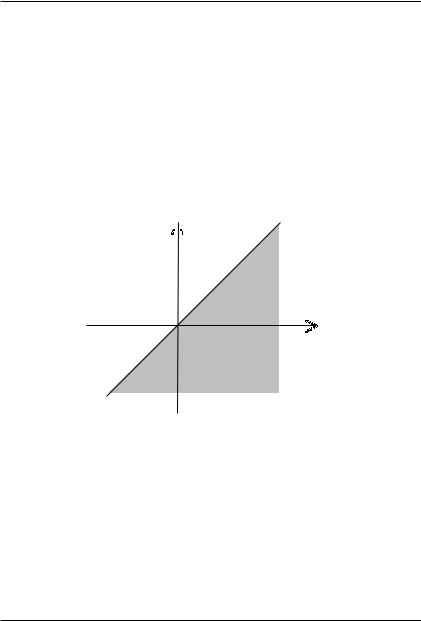
Пример 4.5. Рассмотрим четкие подмножества
называется
~
так и B , с
A = [1, 4] и
B = [3, 5] множества действительных чисел. Пользуясь приведенным
выше определением объединения, получаем, что для четких множеств определение операции объединения приобретает стандартный вид (см. рисунок 4.4). ∙
65
ГЛАВА 4
1 |
|
|
μ A (x) |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
μB (x) |
||
|
|
|
|
|
μ AUB (x) |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
5 |
|
|
|
|
|
|
1 |
|
4 |
|
|
||||
Рис. 4.4. Объединение множеств |
||||||||||||
5. Дополнением нечеткого множества |
~ |
X называется нечеткое |
||||||||||
|
A в |
|||||||||||
¬~
множество A со следующей функцией принадлежности:
μ¬~ (x) = 1− μ ~ (x), x X .
A A
Пример 4.6. Рассмотрим четкое подмножество A = [1, 4] множества
действительных чисел. Пользуясь приведенным выше определением, получаем, что для четких множеств определение операции дополнения множества приобретает стандартный вид (см. рисунок 4.5). ∙
1 |
μ¬A (x) |
|
~ |
x
1 |
4 |
Рис. 4.5. Дополнение множества
Нечеткие отношения. Под четким бинарным отношением, определенным над множеством X , понимается подмножество множества X × X (см. раздел 1.2). Перенося определение нечетких множеств на отношения, определим нечеткое отношение как нечеткое
66
Механизмы стимулирования в активных системах с нечеткой неопределенностью
подмножество |
X |
2 |
. Таким |
|
|
~ |
|||
|
образом, под нечетким отношением R |
||||||||
будем |
понимать |
|
функцию |
принадлежности |
μR (x, y) такую, |
что |
|||
|
|
|
|
|
|
|
|
~ |
|
μR : X ´ X ® [0, 1] . Значение функции принадлежности понимается как |
|||||||||
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
степень выполнения отношения xRy . |
|
|
|||||||
Пример 4.7. Рассмотрим четкое отношение R - «больше, |
либо |
||||||||
равно», |
тогда |
R = {(x, y) |
|
|
x ³ y} . Функция |
принадлежности |
этого |
||
|
|||||||||
четкого бинарного отношения
ì1, x ³ y; μR (x, y) = íî0, x < y.
Множество R изображено на рис. 4.6. ·
 y
y
0 |
x |
|
R
R
Рис. 4.6. Множество пар (x, y) четкого отношения "³"
Свойства нечетких отношений.
1. Рефлексивность: если x X μ ~ (x, x) = 1 , то нечеткое
R
~ |
x X |
μR (x, x) = |
1 |
|
, то |
|
отношение R рефлексивно в смысле Р1; если |
|
|
||||
~ |
|
~ |
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
нечеткое отношение R рефлексивно в смысле Р2. |
μR |
(x, x) = 0 |
то |
|||
2. Антирефлексивность (для Р1): если |
x X |
|||||
|
|
~ |
|
|
|
|
~
нечеткое отношение R антирефлексивно в смысле Р1.
67

ГЛАВА 4
3. |
Симметричность: |
если |
x, y X |
~ |
выполняется |
||||||||
μR (x, y) = μR ( y, x) , |
то |
нечеткое |
отношение |
|
|
называется |
|||||||
|
R |
|
|||||||||||
~ |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
симметричным. |
|
|
x, y X |
из |
μR |
(x, y) > 0 |
следует |
||||||
4. Асимметричность: если |
|||||||||||||
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
μR ( y, x) = 0 , то нечеткое отношение R называется асимметричным. |
|||||||||||||
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Линейность (полнота): нечеткое отношение |
~ |
называется λ - |
|||||||||||
R |
|||||||||||||
линейным в |
смысле |
определения Л1, |
если |
x, y X |
выполняется |
||||||||
max {μR |
(x, y), μR (y, x)}> λ , |
где |
λ Î[0, 1) ; при |
λ = |
0, |
~ |
называется |
||||||
R |
|
||||||||||||
~ |
|
~ |
|
|
|
|
|
|
|
|
|
|
|
слабо |
линейным. |
Если |
x, y X |
|
|
выполняется |
|||||||
max {μR |
(x, y), μR (y, x)}= 1, |
то |
отношение |
~ |
называется |
сильно |
|||||||
R |
|||||||||||||
~ |
|
~ |
|
|
|
|
|
|
|
|
|
|
|
линейным. |
|
|
~ |
|
|
|
|
|
|
|
|
|
|
Нечеткое |
отношение |
называется |
линейным |
|
в |
смысле |
|||||||
R |
|
||||||||||||
определения Л2, если x, y X |
выполняется μR (x, y) = 1- μR (y, x) . |
||||||||||
|
|
|
~ |
|
|
|
~ |
|
~ |
|
~ |
|
|
|
|
|
|
|
определяется |
как отношение, |
|||
6. Отрицание R¢ отношения R |
|
||||||||||
функция |
принадлежности |
которого |
x, y X |
|
определяется |
||||||
μR¢ (x, y) = 1- μR (x, y) . |
|
|
|
|
|
|
|
|
|||
~ |
~ |
|
|
|
|
|
~ |
|
~-1 |
|
|
7. Обратное |
к |
|
|
|
|
|
определяется |
||||
отношению R |
отношение R |
|
|||||||||
x, y X |
выражением μ ~ |
−1 |
(x, y) |
= μ ~ (y, x) . |
|
|
|||||
|
|
|
R |
|
|
R |
|
|
|
|
|
8. Композицией отношений (произведением) называется |
|||||||||||
отношение: |
|
|
|
|
|
|
|
|
|
|
|
К1 - максиминная композиция: |
(x, z), μR (z, y)} ; |
|
|||||||||
|
μR ×R (x, y) = sup min{μR |
|
|||||||||
|
~ |
~ |
|
|
|
|
~ |
|
~ |
|
|
|
1 |
2 |
|
|
zÎX |
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К2 - минимаксная композиция: |
(x, z), μR (z, y)} ; |
|
|||||||||
|
μR ×R (x, y) = inf |
max {μR |
|
||||||||
|
~ |
~ |
|
zÎX |
|
~ |
|
~ |
|
|
|
|
1 |
2 |
|
|
1 |
|
2 |
|
|
||
К3 - максмультипликативная композиция: |
|
|
|||||||||
|
μR ×R (x, y) = sup {μR (x, z)μR (z, y)}. |
|
|
||||||||
|
|
~ |
~ |
|
|
|
~ |
|
~ |
|
|
|
|
1 |
2 |
|
zÎX |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
9. Транзитивность. В соответствии с тремя определениями композиции можно построить три определения транзитивности - (Т1),
~ |
~ |
~ |
(Т2) и (Т3) по следующей схеме: R |
× R |
Í R . Определение максиминной |
транзитивности в случае четких бинарных отношений совпадет с
68

Механизмы стимулирования в активных системах с нечеткой неопределенностью
определением их транзитивности, приведенном в разделе 1.2 (см. также пример 1.3).
Нечетким отношением предпочтения (НОП) назовем нечеткое отношение, удовлетворяющее (Р1), (Л1) и (Т1).
Введем следующее предположение, которое будем считать выполненным на протяжении настоящей главы.
А.10. Предпочтения участников АС являются НОП.
4.2.Модели принятия решений при нечеткой исходной информации
Сформулируем описанное в разделе 1.2 для четких бинарных
отношений предпочтения правило индивидуального рационального
выбора P(RA , A0 ) = {z A0 |
t A0 |
zRA t} в терминах функций |
0 |
|
0 |
принадлежности. Функция принадлежности четкого бинарного отношения предпочтения R задается в виде: μR (x, y) = 1 , если xRy .
Строгая (асимметричная, антирефлексивная, транзитивная) его компонента (отношение строгого предпочтения) определяется функцией принадлежности: μP (x, y) = max{μR (x, y) − μR ( y, x), 0}.
Множество |
альтернатив |
x A0 , доминируемых хотя |
бы одной |
альтернативой |
y A0 , имеет |
функцию принадлежности |
μP ( y, x) . |
Дополнение этого множества, то есть множество альтернатив x A0 , не
доминируемых |
данной альтернативой y A0 , имеет функцию |
принадлежности |
1− μP ( y, x) . Вычисляя пересечение по всем y A0 , |
находим множество альтернатив, недоминируемых по четкому
бинарному отношению RA : |
|
|
0 |
|
|
P(RA0 , A0 ) = inf |
{1− μP |
( y, x)} = 1 − sup μP ( y, x) . |
y A0 |
|
y A0 |
Пример 4.8. Рассмотрим следующее четкое рефлексивное, полное, |
||
транзитивное бинарное отношение (отношение предпочтения) над
множеством |
из трех действий |
y1, |
y2 , y3 , такое, что |
y1 не |
менее |
|
предпочтительно, чем y2 , а y |
2 |
не менее предпочтительно чем |
y3 , y1 |
|||
не менее |
предпочтительно, |
|
чем |
y3 . Это четкое |
отношение |
|
предпочтения удовлетворяет А.10 и приведено в таблице 4.1.
69

ГЛАВА 4
|
y1 |
y2 |
y3 |
y1 |
1 |
1 |
1 |
|
|
|
|
y2 |
0 |
1 |
1 |
|
|
|
|
y3 |
0 |
0 |
1 |
|
|
|
|
Таблица 4.1
Матрица соответствующего ему строгого отношения предпочтения приведена в таблице 4.2.
|
y1 |
y2 |
y3 |
y1 |
0 |
1 |
1 |
|
|
|
|
y2 |
0 |
0 |
1 |
|
|
|
|
y3 |
0 |
0 |
0 |
|
|
|
|
Таблица 4.2
НД |
(x) для |
этого |
отношения предпочтения будет |
||||
Функция μ ~ |
|||||||
R |
|
|
|
|
|
|
|
задаваться таблицей 4.3. |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
y1 |
y2 |
y3 |
|
|
|
μ ~ |
|
1 |
0 |
0 |
|
|
|
НД |
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4.3
Множество недоминируемых действий будет состоять из одного элемента – действия y1 . ∙
Повторим приведенные рассуждения для нечетких множеств. В случае, когда неопределенность в связи действия АЭ и результата деятельности отсутствует, можно считать, что нечеткое отношение
предпочтения задано на множестве возможных действий A : μ ~ (x, y) ,
R
x, y A .
70
