
Курс теории активных систем - Новиков Д.А., Петраков С.Н
..pdf
Механизмы стимулирования в детерминированных активных системах
Функция полезности активного элемента представляется в одном из двух следующих видов
~ |
~ |
- "стимулирование минус затраты"; |
ìσ |
(x, z) - c (z, r) |
|
u(x, z, r, σ (×)) = í~ |
~ |
- "доход минус штрафы". |
îh (z, r) - χ (x, z) |
||
В данной постановке стимулирование (изменение предпочтений АЭ центром) осуществляется путем поощрения или наказания АЭ за выбор тех или иных действий, то есть путем изменения его функции полезности. Таким образом, стимулирование заключается либо в
прибавлении к функции полезности АЭ функции стимулирования (задача I рода), либо в прибавлении к функции полезности АЭ функции
стимулирования и одновременном вычитании этой функции из целевой функции центра (задача стимулирования II рода). В задаче стимулирования второго рода целевая функция центра имеет вид “доход
|
~ |
|
минус затраты на стимулирование”: F(x, |
||
~ |
~ |
~ |
“доход плюс штрафы”: F(x, z, χ (×)) = |
H ( |
|
z, x,
~~ ~
σ(×)) = H (x, z) -σ (x, z) , или
~ |
~ |
z) + χ(x, z) , где |
H (x, z) - |
доход центра, зависящий от результата деятельности АЭ и быть может плана.
Механизм стимулирования (механизм управления в узком смысле)
определяется заданием функции стимулирования ~ : X A R1 M . σ ´ 0 ®
Для постановки задачи стимулирования необходимо ввести на множестве M допустимых механизмов стимулирования критерий их сравнения. В большинстве случаев этот критерий определяется максимальным (либо гарантированным) значением функции полезности центра на множестве выбора АЭ.
Различают прямые и обратные задачи стимулирования. Прямой
задачей стимулирования называется задача поиска оптимального механизма стимулирования, то есть имеющего максимальную эффективность и удовлетворяющего заданным ограничениям: σ~ Î M .
Обратной задачей стимулирования называется задача поиска класса механизмов стимулирования (или оптимального с точки зрения того или иного критерия механизма из этого класса), побуждающих АЭ выбирать некоторое действие (фиксированное или максимально/минимально возможное).
Чтобы ввести критерий эффективности функционирования активной системы, в свою очередь необходимо определить правило рационального выбора активного элемента. В случае, когда неопределенность отсутствует (детерминированная АС), можно
31

ГЛАВА 2
считать, что действие и результат деятельности, а также функции полезности и целевые функции совпадают, то есть z º y; f ( y) º u(z).
Если неопределенность в системе присутствует, будем предполагать, что элемент принимает решение в условиях полной
информированности, то есть, по тому или иному правилу  ·
· устраняет
устраняет
неопределенность1 и определяет свою целевую функцию (переходит от предпочтений, заданных на множестве результатов деятельности к предпочтениям над множеством действий):
f (x, y, r,σ (×)) =  u(x, z, r,σ~(×))
u(x, z, r,σ~(×)) .
.
Например, если в одноэлементной активной системе присутствует интервальная неопределенность, то активный элемент может устранять ее применением МГР, вероятностная неопределенность может устраняться нахождением ожидаемой полезности, нечеткая неопределенность – переходом к индуцированным отношениям предпочтения (см. главы 3 и 4, а также [19]).
Устранив неопределенность, активный элемент выбирает действие, руководствуясь правилом индивидуального рационального выбора:
y* Î Pr (σ (×), A) = Argmax f (x, y, r,σ (×)) .
yÎA
Центр также может устранить неопределенность относительно результата деятельности активного элемента одним из указанных выше способов и определить целевую функцию, зависящую от действия элемента:
|
Y( y,σ |
~ |
~ |
|
|
(×)) = F(z,σ (×)) . |
|
||
Будем |
предполагать, |
что |
выполнена |
гипотеза |
благожелательности (ГБ), то есть элемент выбирает то действие из множества рационального выбора, которое наиболее благоприятно для центра. Тогда эффективность функционирования определится следующим выражением:
K(σ , r) = max Y( y,σ (×)) .
yÎPr (σ (×), A)
Пользуясь этим выражением, можно ввести эффективность механизма стимулирования σ (×) , устранив зависимость K(σ (×), r) от r .
1 В многоэлементной АС использование АЭ тех или иных гипотез о
поведении других игроков также является процедурой устранения неопределенности – см. раздел 1.3 и [8].
32

Механизмы стимулирования в детерминированных активных системах
Если истинное значение параметра r Ω неизвестно центру, то можно устранить эту неопределенность взятием по r гарантированного
результата: |
|
K(σ ) = min |
max Y( y,σ (×)) . |
rÎW yÎPr (σ (×), A) |
|
В случае, когда ГБ не |
выполнена, центру при оценке |
эффективности придется ограничиться гарантированным результатом по множеству рационального выбора:
K(σ ) = min min Y( y,σ (×)) .
rÎW yÎPr (σ (×), A)
Таким образом, мы определили эффективность механизма стимулирования, что позволяет сформулировать прямую задачу стимулирования следующим образом: построить систему
стимулирования σ * Î M такую, что σ * Î Argmax K(σ ) .
σÎM
2.2.Задача синтеза оптимального механизма стимулирования в базовой модели активной системы
Обозначим SP - класс действительнозначных функций q(x) ,
определенных на R1 и удовлетворяющих следующим свойствам:
1) q(x) - непрерывная функция; 2) существует единственная точка
пика (идеальная точка) |
r Î R1 (возможно |
r = +∞ |
либо r = −∞ ) такая, |
|
что q(x) |
строго монотонно возрастает при x < r |
и строго монотонно |
||
убывает |
при x > r ; 3) |
Функция q(x) |
ограничена сверху, то есть |
|
q(r) < +∞ .
Функции, принадлежащие классу SP , называются однопиковыми. Примером однопиковой функции может служить q(x) = − x − r . Точкой
пика при этом может являться значение типа АЭ.
Рассмотрим детерминированную двухуровневую активную систему веерного типа, состоящую из центра и одного активного элемента. Предположим, что точное значение типа r Ω известно и центру, и АЭ. Тогда можно считать, что функции дохода h( y) и затрат
c( y) не зависят от этого |
параметра. Будем исследовать классы |
параметрически заданных |
систем стимулирования: χ(x, y) M - |
33

ГЛАВА 2
функция штрафов, σ (x, y) M - функция стимулирования, где в
качестве параметра1 используется x - план, назначенный АЭ, x Î X - множество допустимых планов АЭ.
Введем следующие предположения.
А.1. A = X R1 .
Предположение А.1 в многоэлементных АС отражает гипотезу независимого поведения (ГНП), в соответствии с которой не существует
глобальных ограничений на совместный выбор стратегий активными элементами.
Для большинства рассматриваемых ниже моделей можно считать,
что A− , A+ : A = X = [A− , A+ ] , где − ∞ < A− << r << A+ < +∞ .
А.2. χ |
- неотрицательная равномерно ограниченная сверху: |
"y Î A, x Î X |
0 £ χ(x, y) £ C < +¥ , кусочно-непрерывная функция. |
Величина C называется ограничением механизма стимулирования.
А.3. h(×) Î SP .
А.4. -c(×) Î SP, c(0) = 0 .
Пусть целевая функция активного элемента имеет вид “доход минус штрафы”: f (x, y) = h( y) - χ(x, y) или “стимулирование минус
затраты”: f (x, y) = σ (x, y) − c( y) .
Будем считать предположения А.1 - А.4 выполненными в ходе
всего последующего изложения. |
|
|
Множество решений игры |
определяются следующим образом: |
|
P(χ) = Arg max {h( y) − χ(x, y)} |
и |
P(σ ) = Arg max {σ (x, y) − c( y)}. |
y A |
|
y A |
Большинство рассуждений в дальнейшем будем проводить для функций штрафов, так как все рассуждения для функций стимулирования могут быть получены по аналогии [19].
Эффективность механизма стимулирования в рамках гипотезы благожелательности, которую мы будем считать выполненной в ходе
последующего изложения, K(χ ) = |
max Φ(χ, y) , а гарантированная |
|
|
|
y P(χ ) |
|
|
|
1 Под системой стимулирования |
χ(x, y) понимается функция от |
|
действия АЭ. Под классом систем стимулирования понимается
объединение систем стимулирования по некоторому множеству значений параметра.
34

Механизмы стимулирования в детерминированных активных системах
эффективность K Γ (χ ) = min F(χ, y) , где Φ(χ, y) - целевая функция
y P(χ )
центра. Задача стимулирования заключается в выборе механизма стимулирования χ M , имеющего максимальную эффективность:
χ Î Argmax K(χ ) .
χM
Обозначим PM = UP(χ ) - максимальное множество реализуемых
χM
действий. Класс M систем стимулирования назовем оптимальным
в M , если выполнено P = UP(χ ) = PM .
χ
Система штрафов (стимулирования) следующего вида:
ì |
æ£ö |
|
|
ç |
÷ |
ï0, yç |
÷x; |
|
ï |
è³ø |
|
χC (x, y) = í |
æ |
>ö |
ï |
||
|
ç |
÷ |
ïC, yç |
÷x |
|
î |
è |
<ø |
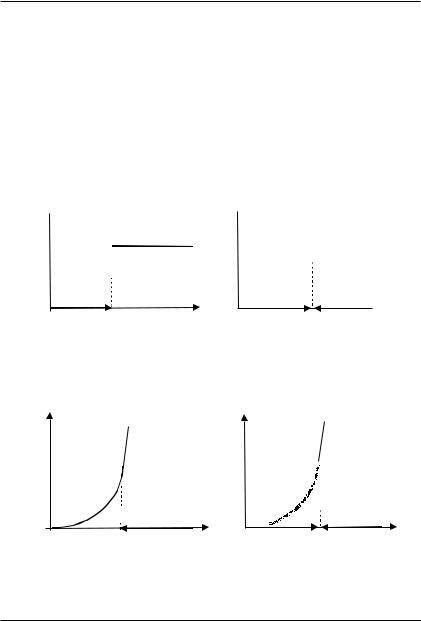
называется скачкообразной системой (С-типа) стимулирования (см.
рисунок 2.2). Множество систем стимулирования С-типа при всех возможных x X обозначим M C Í M .
Систему стимулирования:
|
|
|
|
ì0, y = x; |
|
|
|
|
|
|
|
|
|
|
χQC (x, y) = í |
|
|
|
|
|
|
|
|
|
|
|
|
îC, y ¹ x |
|
|
|
|
|
|
|
назовем квазискачкообразной ( QC -типа) (см. рисунок 2.3). |
|
||||||||||
|
Введем также компенсаторные ( K |
|
- |
|
|
|
типа) |
системы |
|||
стимулирования, имеющие вид: |
|
|
|
|
|
|
|
|
|||
|
ì |
[hmax - C], y Î[ y |
− |
, y |
+ |
]; |
|
||||
|
|
|
ïh( y) - |
|
|
|
|||||
|
|
|
χ K ( y) = í |
|
|
|
|
|
|
|
|
|
|
|
ïC, y Î[ y − , y + ]. |
|
|
|
|
|
|
|
|
|
î |
|
|
|
|
|
|
|
|
||
где |
hmax = h(r) , |
y− = min{y Î A |
|
h( y) ³ h(r) - C} , |
|||||||
|
|||||||||||
y + |
= max{y Î A |
|
h( y) ³ h(r) - C} |
- соответственно |
|
левая |
и правая |
||||
|
|
||||||||||
границы множества действий, реализуемых при заданных ограничениях механизма стимулирования, и квазикомпенсаторные ( QK -типа)
системы стимулирования, определяемые следующим образом:
35
ГЛАВА 2
χQK (x, y) = ìh( y) - [hmax - C], y = x;
íîC, y ¹ x.
Множество систем стимулирования K - типа обозначим M K ( M K = M K (h(×)) . Графики компенсаторных функций стимулирования
при представлении целевой функции АЭ в виде «стимулирование минус затраты» и параболических затратах приведены на рисунках 2.4 и 2.5.
Вид целевой функции АЭ (представленной в виде “стимулирование минус затраты”) при использовании центром скачкообразной системы стимулирования приведен на рисунке 2.6.
 σ(y)
σ(y)
C 











0 x
Рис. 2.2. Скачкообразная
система стимулирования
σ(y) c(y)
c(x)
0 x
 σ(y)
σ(y)
C .
y |
y |
0 x
x 
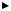
Рис.2.3. Квазискачкообразная
система стимулирования
σ(y) c(y) c(x)













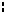 .
.
y |
y |
0 x
x
Рис.2.4. |
Компенсаторная |
Рис.2.5. Квазикомпенсаторная |
система стимулирования |
система стимулирования |
|
36

Механизмы стимулирования в детерминированных активных системах
C-c(x) |
x |
y |
|
|
y+ |
-С |
|
f(y) |
|
|
|
|
|
-c(y) |
Рис. 2.6. Целевая функция АЭ при
использовании центром системы стимулирования С-типа
Максимальное множество действий АЭ, реализуемых при заданных ограничениях механизма стимулирования, определяется следующим утверждением.
Теорема 2.1. Класс систем стимулирования С-типа имеет при данных ограничениях C механизма стимулирования максимальное
множество реализуемых действий P |
= P |
= [ y− |
, y+ ] . |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
C |
M |
y [ y− , y+ ] |
|
|
|
|
|
|
|
||||
Доказательство. |
Любое |
|
действие |
реализуемо |
|||||||||||||||||||
системой стимулирования |
χ |
C |
( y , y) , то есть P |
|
= [y− |
, y+ ]. Докажем, |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
||
что PM = PC . |
Предположим, |
что существует система стимулирования |
|||||||||||||||||||||
~ |
|
|
|
|
|
|
А.2 |
и |
реализующая |
действие |
|
~ |
не |
||||||||||
χ ( y) , удовлетворяющая |
|
y , |
|||||||||||||||||||||
принадлежащее множеству |
PC . Для определенности положим |
~ |
|
+ |
. |
||||||||||||||||||
y > y |
|
||||||||||||||||||||||
Тогда по определению множества реализуемых действий: |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
~ |
~ ~ |
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
h( y) - χ |
( y) ³ h( y) |
- χ ( y), "y Î A . |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
~ |
~ ~ |
³ h(r) |
|
~ |
|
|
|
|
|
|
|
|
|
Рассмотрим y = r . Тогда h( y) - χ ( y) |
- χ (r) . |
~ |
|
|
|
|
|
|
|
||||||||||||||
Так как |
|
y |
+ |
³ r |
и |
мы |
предположили, |
|
что |
> y |
+ |
, |
то |
по |
|||||||||
|
|
|
|
y |
|
||||||||||||||||||
определению y |
+ |
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и А.3: h(r) - h(y) > C . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Следовательно, имеет |
|
|
|
~ |
|
~ ~ |
|
|
что |
противоречит |
|||||||||||||
место χ |
( r) - χ (y) > C , |
||||||||||||||||||||||
~ |
< y |
− |
рассматривается полностью аналогично. · |
|
|
|
|
|
|||||||||||||||
А.2. Случай y |
|
|
|
|
|
|
|||||||||||||||||
Из вида задачи стимулирования первого рода следует, что чем шире множество действий, реализуемых тем или иным классом систем
37

ГЛАВА 2
стимулирования, тем выше эффективность стимулирования. Следовательно имеет место следующее утверждение.
Следствие. Классы систем стимулирования: C, QC, K и QK - типа
оптимальны в M .
Детерминированная задача стимулирования второго рода.
Пусть в системе имеется единственный АЭ, целевая функция которого имеет вид “доход минус штрафы”, а целевая функция центра представлена в виде:
Φ(x, y) = H ( y) + χ(x, y) .
Очевидно, действия, лежащие вне множества [y− , y+ ] не
реализуемы при заданных ограничениях механизма стимулирования. Максимальные штрафы, допустимые при реализации действия
y [y− , y+ ] , определяются функцией χmax ( y) = h( y) − hmax + C .
Тогда необходимо найти действие y [y− , y+ ] такое, что оно доставит максимум функции H ( y) + χmax ( y) . То есть, оптимальным
реализуемым действием будет
y Argmax {H ( y) + h(y)} .
y [ y − , y + ]
При этом оптимальной будет квазикомпенсаторная или компенсаторная система стимулирования.
Если ограничения на стимулирование отсутствуют, то есть C =+∞,
то y Argmax {H ( y) + h( y)} . Если целевая функция АЭ представлена
y A
в виде «стимулирование минус затраты», то y Argmax {H ( y) − c( y)} .
y [ y− , y+ ]
Следует подчеркнуть, что и в задаче первого рода, и в задаче второго рода, мы фактически "угадали" оптимальное решение, не решая задачу в лоб (хотя существует теорема Ю.Б.Гермейера, дающая
решение задачи синтеза оптимальных управлений для общего случая иерархической игры Г2 [10])1. Существенную помощь при этом оказала
1 Следует признать, что для теории активных систем во многих случаях характерно именно угадывание решений (исходя из интуиции, содержательных рассуждений и т.д.), а также стремление получить аналитическое решение. Объяснения этому достаточно прозрачны: исследование формальной модели социально-экономической системы не
38

Механизмы стимулирования в детерминированных активных системах
идея анализа множеств реализуемых действий. Альтернативным подходом является анализ минимальных затрат на стимулирование, к описанию которого мы и переходим.
Пусть целевая функция АЭ имеет вид «стимулирование минус затраты». Минимальными затратами на стимулирование по реализации действия y Î PM в классе допустимых систем стимулирования M
называется следующая величина: σ min (y) = min {σ(y) | y Î P(σ)}, то
σ M
есть минимальное допустимое вознаграждение, которое побудит АЭ выбрать заданное действие. Для тех действий, которые в рамках предположения А.2 не могут быть реализованы в классе M, положим минимальные затраты на стимулирование равными бесконечности: σ min (y) =+∞, y Î A \ PM. Очевидно, что в рамках предположения А.4
"y Î PM σ min (y) = с(y).
Минимальные затраты на стимулирование являются чрезвычайно важным понятием. Их анализ позволяет решать задачу синтеза оптимальной функции стимулирования, изучать свойства оптимального решения и т.д. Если для задачи стимулирования первого рода критерием
сравнения эффективностей систем стимулирования служат максимальные множества реализуемых ими действий, то минимальные
затраты на стимулирование являются таким критерием одновременно для задач и первого, и второго рода. Обоснуем это утверждение. Для этого обозначим максимальную в классе M1 Í M эффективность
управления KM1 = max K(σ). σ Î M1
Теорема 2.2. Пусть M1 Í M, M2 Í M - два подкласса допустимых систем стимулирования и выполнено: " y Î A σ (y) £ σ min 2 (y) .
Тогда для задач первого и второго рода KM1 ³ KM2.
Доказательство. Обозначим Pi = U P(σ), i = 1,2, - максимальные
σ Mi
множества действий, реализуемых в соответствующих классах систем стимулирования. Пусть y PM2 . Тогда, так как " y Î A
является самоцелью исследователя операций - его задача заключается в том, чтобы предложить максимально адекватное
действительности содержательно интерпретируемое решение задачи управления.
39

ГЛАВА 2
σ min1(y) £σ min 2 (y) , то по определению минимальных затрат на стимулирование σ min1(y) < +∞, то есть y PM1 . Другими словами, если
выполнено условие теоремы, то в силу определения минимальных затрат на стимулирование имеет место P2 Í P1, то есть системы стимулирования, характеризуемые меньшими затратами на стимулирование, реализуют большие множества действий, что доказывает утверждение теоремы для задач первого рода.
Доказать справедливость утверждения теоремы можно и не прибегая к явному анализу множеств реализуемых действий. Для этого рассмотрим задачу стимулирования первого рода. Обозначим
σ2 |
= arg max |
{ max H(y)}, y2 = arg |
max H(y). |
|
σ Î M 2 |
y Î P(σ ) |
y Î P(σ 2 ) |
Тогда KM2 = H(y2) и существует σ1 Î M1 такое, что y2 Î P(σ1),
следовательно, KM1 ³ H(y2) = KM2.
Рассмотрим задачу стимулирования второго рода. Эффективность
стимулирования может быть определена и через минимальные затраты на стимулирование, причем имеет место:
KM2 |
= max {H(y) - σ min 2 |
(y) } £ max {H(y) - σ min1( y) } = KM1. · |
|
y A |
y A |
Обратные задачи стимулирования первого и второго рода заключаются в поиске ограничений механизма стимулирования, при которых реализуется заданное действие. В случае, если целевая функция АЭ задается в виде «доход минус штрафы», максимальные
штрафы, необходимые для реализации заданного действия y* , очевидно, определяются χmax ( y) . Зависимость множества реализуемых
действий от ограничений механизма стимулирования определяется следующей теоремой.
Теорема 2.3. С увеличением ограничений механизма стимулирования C максимальное множество реализуемых действий
PM не сужается.
Доказательство. Справедливость утверждения теоремы следует из определения множества действий, реализуемых в рамках введенных предположений системами стимулирования из класса M . ·
Перечислив общие результаты решения задачи синтеза оптимальной функции стимулирования (теоремы 2.1 – 2.3), рассмотрим
в качестве частных случаев пропорциональные системы
40
