2.2.1. Пропорции и целостность восприятия

В эпоху Ренессанса красивые пропорции называли божественными. Пропорции в костюме - это как бы его внутренняя красота, она «невидима непосредственно, но весьма ощутима, подобно красоте духовной». В основе пропорции лежит число. Красивая пропорция - это число, пропущенное через сознание художника.

Каждый элемент формы таит в себе проблему пропорций, т. к. соотношение между длиной, шириной и глубиной требует постоянного поиска. С увеличением числа элементов возникает проблема упорядочивания многих вещей при определенном соотношении размеров.

Найти гармонию помогает знание основных систем пропорций. Пропорции объемной структуры делятся на модульные, где взаимосвязь частей и целого выражается на повторении заданного размера (модуля) и на геометрические.

Простые пропорциональные отношения 2:3, 3:4, 3:5 и т. д. содержат в себе модуль, укладывающийся в целое. Основой гармоничности простых отношениях является ясная соразмерность линейных и объемных величин, где модуль служит единицей измерения формы, его внутренней мерой. Наиболее четко зрительная соразмерность выражается отношением 1:1, где модулем служит квадрат, но эта соразмерность инертна, статична, ма­ловыразительна, так как сравниваемые величины равноценны. От пра­вильно найденного модуля зависит общая гармония формы. Поэтому вели­чина модуля в больших изделиях должна быть большей, в небольших -меньшей. Однако, чем больше величина модуля, тем статичней и «скуч­нее» пропорциональные отношения в целом (например, величина лифа платья как модуля упрощает общие пропорциональные отношения как 1:1 или 1:2). С другой стороны, пределом простых отношений являются числа до восьми. Их можно определить как предел ясного восприятия сораз­мерности величин, воспринимаемых человеком. Среди простых отношений наиболее выразительны отношения: 1:3, 2:5 и т.д.

Геометрические пропорции строятся на равенстве отношений и про­являются в геометрическом подобии членений форм. Частным случаем геометрической пропорции является пропорция золотого сечения. Исходя из принципа золотого сечения, можно построить прямоугольник, стороны которого относятся как 1,62/1. Такой прямоугольник называется «золотым», динамичным. Он обладает тем свойством, что если отсечь от него квадрат, то оставшаяся часть окажется прямоугольником, подобным первоначальному. Наряду с золотым сечением наиболее часто в природе, изобразительном и т прикладном искусстве встречаются пропорции с иррациональными соотношениями: √3,√5,√7. Прямоугольники с таким соотношением сторон распадаются на элементы, строение которых повторяет строение целого.

Анализируя исторический костюм, мы часто сталкиваемся с различными вариациями пропорции золотого сечения. Так, например, русские народные костюмы, которые проанализированы способом обмера их частей, построены с учетом принципа золотого сечения на основании пропорций фигуры человека. Возможно, народные мас­тера в поисках гармонии часто интуитивно «выходили» именно на эти |пропорциональные отношения. Леонардо да Винчи разработал пропорцию, которая получила название «квадратура круга». Он связал масштаб про­порций с квадратом, длина которого была определена высотой тела и включала в себя систему деления, позволяющую установить размеры с по­мощью циркуля в отношениях от 1/2, 1/96 фигуры (рис. 14). Эта пропорция легла в основу европейского канона и использовалась зодчими и художни­ками эпохи Ренессанса.

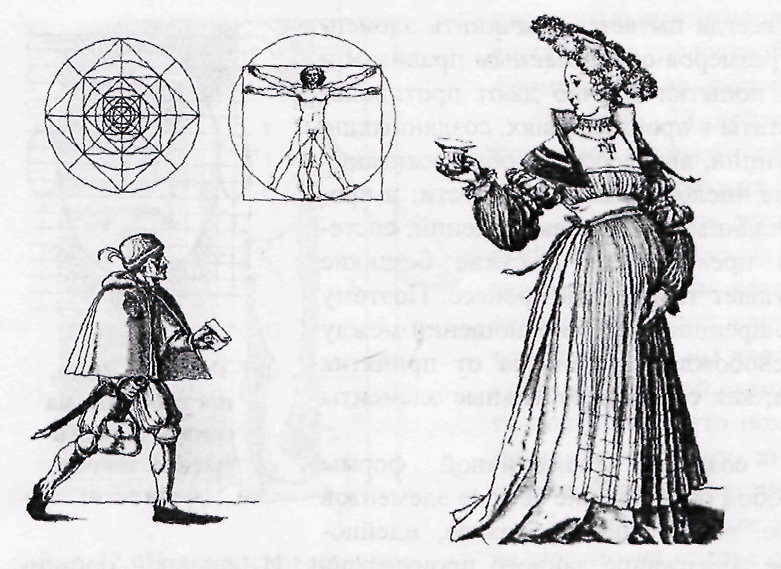
Рис. 14. Квадратура круга Леонардо да Винчи и костюмы, построенные

на ее основе

В Древней Греции, взятые за основу пропорцио­нальные отношения золотого сечения «пропитали» не только архитектуру, но и скульптуру костюма (рис. 15).

Понимая костюм как «эхо человеческого тела», греки строго соблюдали в нем эти пропорции. Линии талии в их костюме всегда подчеркивались поясом несколько выше ее естественного положения, что соответствовало пропорции золотого сечения.

Дизайнер всегда увлечен поиском красивых пропорциональных отношений. Пропорции в значительной степени определяют целостность объемной структуры изделия. Как бы хороши не были сами по себе части целого, но если отсутствует четка» система в их организации, дизайнер не достигнет образной выразительности изделия.

Интерес представляет мнение Корбюзье о необходимости создания новой системы измерений. Системы, которая бы способствовала поиску не только полезных, но и красивых пропорций. Корбюзье задавал вопрос:

Рис. 15. Пропорция золотого сечения в архитектуре, скульптуре и

костюме Древней Греции

«Если бы появился какой-нибудь линейный измеритель, подобный систе­мам музыкальной записи, не облегчился бы ряд проблем?» И в качестве такового предлагает свой модулор. Модулор - это такой измерительный прибор, в основе которого лежит человеческий рост и математика. На рис. 16 показан этот прибор. В его основу заложены рост человека и золо­тое сечение. Здесь исходные единицы измерения связаны с членением че­ловека. Они закономерно увеличиваются и уменьшаются вверх и вниз. Каждое последующее членение связано с предыдущим золотым сечением. На вопрос о достоинствах модулора Корбюзье отвечал: «Метр - это цифры без реального содержания: сантиметр, дециметр, метр - это только обозначение десятичной системы. Цифры модулора - это действительно размеры. Они - факты. Они являются результатом выбора между бесконеч­ным количеством величин». Корбюзье разработал систему предпочтительных чисел, ввел в систему наших измерений два начала - человеческое и эстетическое. Эйнштейн сравнивал модулор с гаммой пропорций, которая «делает плохое трудным, а хорошее легким». Корбюзье писал: «Модулор -это гамма. Музыкант располагает гаммой и создает музыку по своим спо­собностям - банальную или красивую». Модулор - гамма. Но гамма - это еще не музыка.

Музыка связана с движением и временем: течет время, движутся зву­ки, меняя тембр, окраску, убывая и нарастая. Костюм - тоже движение. Ему свойственна динамика, ритм, пластика и невозможно подобрать такую систему пропорций, которая подошла бы к любому случаю и соответство­вала абсолюту.

Работая над поиском соотношений размеров формы, дизайнер в пер­вую очередь должен определить отдельный (главный) элемент, а потом уже находить его взаимосвязь с другими. Он должен постоянно трениро­вать чувство пропорции, чтобы уметь оценить отношение элементов, ощущать - когда напряженность угрожает гармонии, избегать вялых соот­ношений, ведущих к однообразию (прил. 1).

Р ис. 16. Модулор Корбюзье

2.2.2. Масштабность и масса

Выразительность композиции, ее читаемость находятся в зависимости от того, в какой мере создается зрительное движение формы в границах силуэта костюма: от подчиненных частей к главной части или к компози­ционному центру. Для подчеркивания главного элемента в костюме зри­тельное движение должно быть организовано так, что на какую бы часть костюма ни был обращен взгляд, динамика неизбежно указала бы ту часть, которая выделена дизайнером. Такое движение создается благодаря свойствам пластической линий, ритма и принципа неравных отношений в членении: сходства и контраста. Чем лучше организовано это движение, тем яснее читается композиция костюма.

Для создания зрительного движения в дизайне костюма используют масштаб (принцип неравных отношений частей одежды), когда контраст­ное противопоставление одних частей формы другим создают ярко выра­женное различие и противопоставление частей. Здесь под масштабностью понимается отношение величины формы одежды к фигуре человека, соот­ношение величины частей формы между собой и их отношение ко всей форме одежды. Выбор отношения величины частей одежды к общей ве­личине ее формы - один из способов создания выразительности, ис­пользуемых в композиции (рис. 17). Согласованность размерных показа­телей всех составляющих определяет степень грамотности построения формы и его пластической выразительности. Возможности гармонизации формы средствами масштабных величин заключаются в поиске вариаций с тремя группами величин: мелкими, средними, большими. Бесчисленная вариантность этих групп может быть обеспечена по закону трехкомпо-нентности, когда для убедительного выражения сложного и разнообраз­ного движения формы достаточно и необходимо гармонизировать три ее компонента (три величины, три формы, три фактуры и т. п.). Число «три» является тем минимальным числом, которое позволяет достаточно четко определить разнообразие какого-либо явления. Именно к трехкомпонент-ной классификации подсознательно стремится человек, когда хочет объяс­нить многообразие окружающих его явлений. Например, пространство и объемная форма характеризуются длиной, шириной и высотой; положение линии может быть вертикальным, горизонтальным и наклонным и т. д.

Трудно создать целостную и легко воспринимаемую форму костюма, если в ней менее или более трех компонентов. Другими словами, сравни­тельно ограниченное число элементов формы позволяет создать кажущее­ся разнообразие и придать целостность их движению (рис. 18).

Рис. 17, Принцип неравных отношений частей формы в костюме

В усилении выразительности формы большую роль играет контраст малой или большой величины относительно общей формы, т. е. утвержде­ние ясного приоритета большей формы над меньшими. Масштабность в связи с этим связана с возникающими отношениями масс. Масса одежды обладает «тяжестью», весомостью, которая в зависимости от тех или иных условий выражается в большей или меньшей степени. В расположении масс частей одежды при ее членении на верхнюю и нижнюю части возникает необходимость их зрительного равновесия. Это нужно для того, чтобы вся форма в целом выглядела устойчивой. Масштабность как средство выражения гармонии не может существовать без уравновешен­ности и устойчивости. Но, иногда, в зависимости от назначения костюма и творческих замыслов дизайнера, требованиями равновесия пренебрегают. В этом случае в костюме специально создается ощущение динамики, неустойчивости формы, нарушающей все земные физические законы. Одна­ко следует оговориться, что любое нарушение правил и законов должно быть уместным и своевременным.

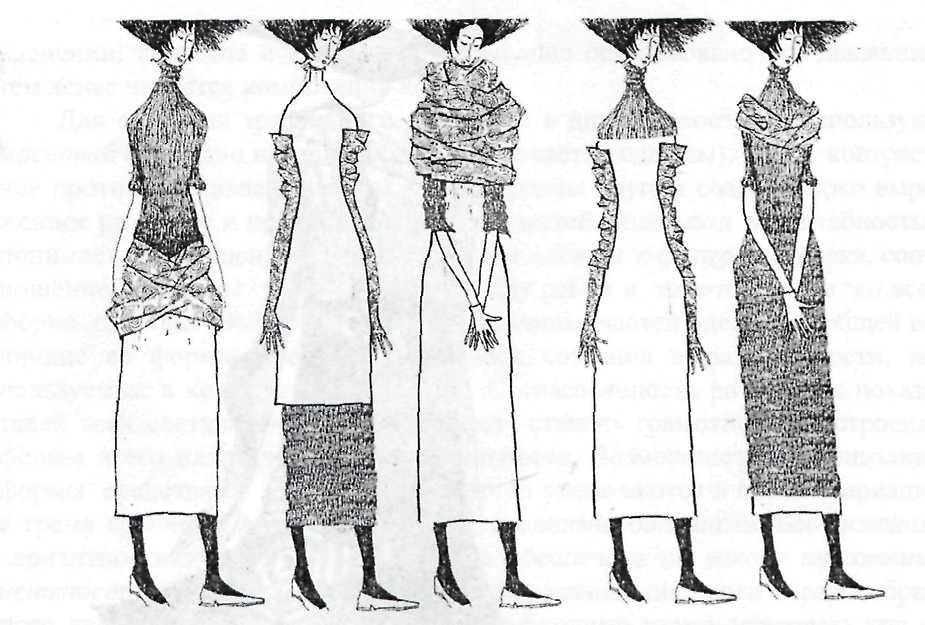
Рис. 18. Закон трехкомпонентности в костюме