4.2.4. Цифровые компараторы
Для сравнения двух сигналов используются компараторы (от англ. compare – сравнить). Они позволяют дать ответы на вопросы, равны или не равны два сигнала; если не равны, то какой из этих сигналов больше. Для сравнения двух двоичных чисел нужен цифровой компаратор. В табл. 4.7 указана связь между сигналами на выходах и входах компаратора при сравнении одноразрядных чисел а и b, которые могут быть равны 1 или 0. На соответствующем выходе появляется логическая 1, когда в указанном соотношении находятся сигналы на входах. Так, если а = 1, b = 1 (числа одинаковы), то функция, характеризующая равенство чисел, Fa = b = 1, а функции, характеризующие их неравенство, Fa>b = 0 и Fa<b = 0. Аналогично заполняются другие строки таблицы.
Таблица 4.7
Входные и выходные сигналы цифрового компаратора
Входы |
Выходы |
|||
а |
b |
Fa>b |
Fa = b |
Fa<b |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
По известным правилам на основании табл. 4.7 можно записать следующие логические функции, характеризующие соотношение одноразрядных чисел:
Fa>b
=
;
Fa=b
=
;
Fa<b
=
.
Если значения а и b таковы, что правая часть функции равна 1, то соотношение, указанное в левой части, выполняется. Если правая часть функции равна 0, то соотношение между а и b противоположно указанному.
Схема одноразрядного компаратора, реализующая приведенные функции, изображена на рис. 4.13.
Остановимся подробнее на функции равенства чисел Fa=b, или функции «Равнозначность». По смыслу она противоположна функции Fab «Неравнозначность» (исключающее ИЛИ). Поскольку
,
.
Следовательно, проверку равенства пары одноименных разрядов двух чисел можно осуществить, используя логический элемент «Равнозначность» (рис. 4.14, а) или «Неравнозначность», дополненный инвертором (рис. 4.14, б).
Числа А и В равны, если их одноименные разряды содержат одинаковые цифры (а0 = b0 И а1 = b1 И ... И аn – 1 = bn – 1), т.е. функция, характеризующая соотношение чисел, должна быть конъюнкцией функций, характеризующих соотношение цифр в их одноименных разрядах:
FA=B = Fa0=b0 v Fa1=b1 v... v Fan-1=bn-1.
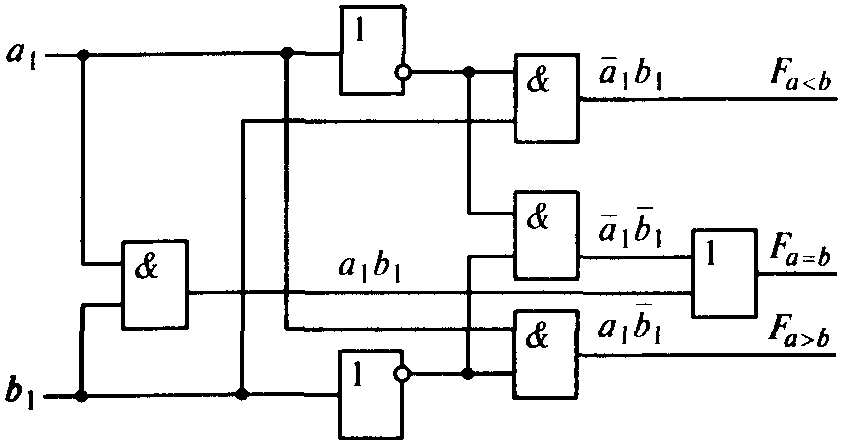
Рис. 4.13. Схема цифрового одноразрядного компаратора
Рис. 4.14. Проверка равенства разрядов:
а – на логическом элементе «Равнозначность»; б – на логическом элементе «Неравнозначность»
Когда цифры в одноименных разрядах чисел А и В одинаковы, на выходах всех элементов «Равнозначность» (рис. 4.15, а) логические 1 и FA=B = 1. Если хотя бы в одной паре разрядов находятся разные цифры, то на выходе соответствующего элемента «Равнозначность» будет логический 0 и FA=B – 0, что указывает на неравенство чисел А и В.
Если цифры в одноименных разрядах чисел А и В одинаковые, то на выходах всех элементов «Неравнозначность» (рис. 4.15, б) логические 0, поэтому на выходе дизъюнктора – 0, а на выходе инвертора – 1,т.е. FA=B = 1.
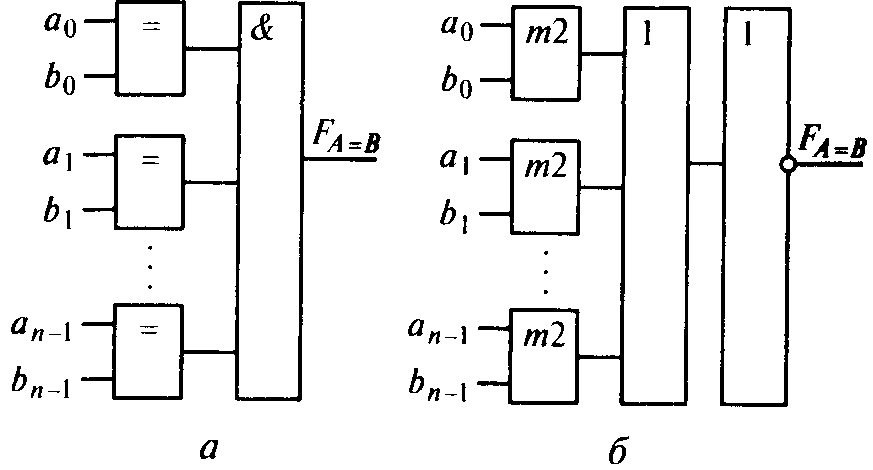
Рис. 4.15. Поразрядное сравнение:
а – на логических элементах «Равнозначность»; б – на логических элементах «Неравнозначность»
На рис. 4.16 приведены условные обозначения компараторов и показан способ наращивания их разрядности. Каждый из изображенных компараторов предназначен для сравнения двух четырехразрядных чисел и имеет выходы А > В, А = В и А < В. Аналогичные входы служат для наращивания разрядности компараторов. Результат сравнения младших разрядов отражается на выходах компаратора K1; на одном из них появляется 1, на других – 0. Компаратор K2 воспринимает этот результат, с учетом которого формируется окончательный результат сравнения. Подобным образом можно осуществлять дальнейшее наращивание разрядности. Указанные потенциалы на входах компаратора K1 младших разрядов обеспечивают правильное функционирование многокаскадного компаратора на данных микросхемах.
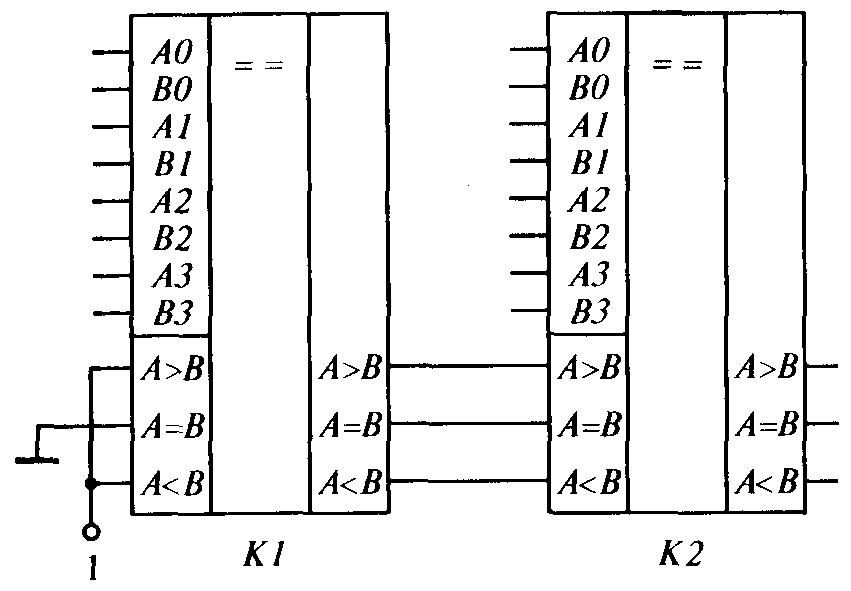
Рис. 4.16. Соединение цифровых компараторов для наращивания их разрядности