6.1.5. Трехфазный асинхронный двигатель как элемент исполнительных механизмов

В качестве трехфазных асинхронных исполнительных двигателей применяют асинхронные двигатели с массивным ротором. Они надежны в работе, просты в изготовлении, позволяют изменением подводимого к двигателю напряжения на статорную обмотку регулировать в диапазоне 20% частоту вращения ротора. В качестве регуляторов напряжения используют управляемые магнитные усилители, инверторы или преобразователи частоты. Механические характеристики двигателя с массивным ротором, полученные при различных напряжениях на статоре, приведены на рис. 6.12. Момент, развиваемый трехфазным асинхронным двигателем:

, (6.7)

где – угловая скорость поля статора; U – напряжение на статоре; R₁, X₁ – активное и индуктивное сопротивления обмотки статора; R'₂, X'₂ – активное и индуктивное сопротивления ротора, приведенные к обмотке статора;

– скольжение ротора двигателя.

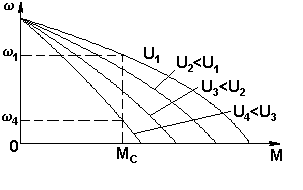
Рис. 6.12

Для зоны рабочих скольжений, когда S мало, в знаменателе выражения (6.7) можно пренебречь составляющими с S и S².

Тогда уравнение момента двигателя представляется линейной зависимостью:

. (6.8)

Из уравнения (6.8) можно получить для установившегося режима M_д = M_с уравнение механической характеристики:

, (6.9)

где – синхронная угловая скорость ротора;

f – частота питающего переменного тока;

P – число пар полюсов двигателя.

В соответствии с уравнением (6.9) на рис. 6.13 приведены механические характеристики трехфазного асинхронного двигателя в зоне рабочих скольжений (сплошные линии) при регулировании частоты f переменного тока на статоре (рис. 6.13, а), при регулировании напряжения U на статоре (рис. 6.13, б), при изменении числа пар полюсов P_дв=1 до P_дв=2 (рис. 6.13, в), при регулировании сопротивления в цепи ротора (рис. 6.13, г).

При определении передаточной функции трехфазного асинхронного двигателя пренебрегаем электромагнитными переходными процессами из-за их кратковременности по сравнению с механическими переходными процессами вращающихся масс. При этом электромеханические переходные процессы двигателя, управляемого напряжением на статоре, характеризуются уравнением:

, (6.10)

где – уравнение механической характеристики в линейной её части;

M_C() – механическая характеристика рабочей машины – рис. 6.14.

Рис. 6.13

1 – M_C = const типична для подъёмных механизмов, транспортных установок;

2 – – типична для мотальных установок;

3 – – вентиляторная характеристика

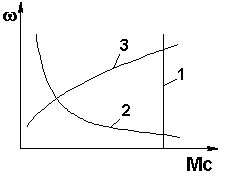
Рис. 6.14

В результате линеаризации уравнения (6.10) получим уравнение асинхронного двигателя в отклонениях переменных:

, (6.11)

где выражения в скобках с индексом «0» представляют числа.

Линейное уравнение (6.11), преобразованное по Лапласу, запишем в операторной форме:

,

тогда передаточная функция:

,

где – постоянная времени;

– коэффициент усиления.

Для рабочих машин М_с = const, и значения параметров будут:

; .

Если рассматривать в качестве выходной координаты угол поворота его вала, как это имеет место в исполнительных механизмах, и учитывая , передаточная функция двигателя будет:

.

При определении передаточной функции трехфазного асинхронного двигателя управляемого изменением частоты переменного тока на статоре, пренебрегаем электромагнитными переходными процессами из-за их кратковременности по сравнению с механическими переходными процессами вращающихся масс, которые характеризуются уравнением:

,

где – уравнение механической характеристики двигателя в линейной её части;

– синхронная угловая скорость при f_Н = 50 Гц.

Введем следующие координаты, характеризующие движение асинхронного двигателя при частотном управлении: – относительная частота, f_Н = 50 Гц, _С – синхронная угловая скорость при частоте , , – фиктивное скольжение двигателя. При этих условиях запишем следующие соотношения для асинхронного двигателя:

.

Полагая, что между вращающим моментом двигателя и фиктивным скольжением S_Ф существует линейная зависимость:

,

запишем уравнение движения двигателя в отклонениях переменных при М_С = const в виде:

.

Преобразуем по Лапласу линейное дифференциальное уравнение при нулевых начальных условиях и запишем его в операторной форме:

.

Произведя разделение переменных, после простых преобразований получим операторное уравнение в виде:

,

где

Передаточная функция асинхронного двигателя, управляемого изменением частоты переменного тока на статоре, будет:

,

что соответствует интегро-дифференцирующему звену.