7.3.2. Теоретико-ігрова модель вибору

структури портфеля при невідомому

розподілі ймовірності

Як уже зазначалось, при побудові класифікатора інформацій­них ситуацій (п. 5.1) у полі I₄ розподіл імовірності станів еконо­мічного середовища невідомий, тобто компоненти вектора Q = {q_i.,….. ,q_n) є невідомими, але при цьому задовольняють умовам (5.1)—(5.2). У полі третьої інформаційної ситуації (Iз), окрім (5.1)—(5.2), невідомі значення компонент вектора Q задовольня­ють ще певній системі обмежень. У випадку I₂, окрім (5.1)—(5.2), треба враховувати, що невідомі значення компонентів вектора Q є функціями від певної сукупності параметрів, тобто що — множина допустимих значень вектора параметрів А тому, визначивши значення норм прибутків співвідношення (7.43), (7.44) та (7.45) можна розглядати як залежності відповідно споді­ваних норм прибутку m_i, дисперсій та коваріацій від змінних (ймовірностей станів економічно­го середовища). Враховуючи, що доходимо

висновку, що можливі значення кількісних показників належать певним скінченним проміжкам. Так, сподівані норми при­бутку (7.43) належать відрізкам, що визначаються нерівностями

середньоквадратичні відхилення (7.14) — відрізкам

З урахуванням наведених міркувань, такі кількісні показники портфеля активів із структурою x = (x₁;...;x_N), як його сподівана норма прибутку m_п та ступінь ризику (дисперсія) , що задані згі­дно з (7.3) та (7.4) відповідно, можна розглядати як функції, що за­лежать від n + N змінних, котрі для зручності об'єднаємо у вектор (Q;X) = (q₁;...;q_n;x₁;...;x_n). Принагідно нагадуємо, що компоненти вектора (Q; X) задовольняють умовам (5.1)—(5.2) та (7.48)—(7.49).

Розглядаючи як ще один критерій принцип максимальної не­визначеності Гіббса—Джейнса, в полі четвертої інформаційної ситуації (I₄) модель задачі щодо вибору структури портфеля мо­же задаватись у вигляді такої оптимізаційної задачі:

(7.56)

(7.57)

(7.58)

при виконанні обмежень

(7.59)

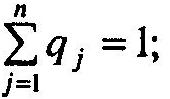(7.60)

(7.61)

де У свою чергу, є функціями величин

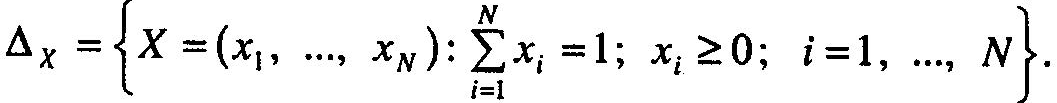
При розв'язанні багатокритеріальних задач (задача (7.56)— (7.61) є трикритеріальною) [123] слід відмовитись від пошуку рі­шення, яке було б найкращим одночасно згідно з усіма критерія­ми, оскільки воно може просто і не існувати. А це означає, що пошук прийнятного (компромісного) рішення слід здійснювати серед ефективних портфелів, для яких будь-яке інше рішення, що є кращим за одним критерієм, обов'язково буде гіршим з позиції інших (принаймні, хоча б одного з них).

Введемо поняття ефективного портфеля, що є характерним для I₄.

Портфель зі структурою називатимемо ефектив­ним згідно з концепцією Марковіца для інформаційної ситуації I₄, якщо існує хоча б один вектор Парето задачі (7.56)—(7.61) вигляду:

Згідно з даним означенням множина Парето будується при фі­ксованому розподілі Скориставшись цією методи­кою і зафіксувавши певне значення вектора (тим самим зафіксувавши певний рівень критерія (7.58)), розв'яжемо відпові­дну двокритеріальну задачу, тобто отримаємо множину векторів Парето:

(7.62)

Множина критеріальних оцінок у тривимірному критеріальному просторі утворюватиме плоску криву у площині Z = H(Q) (тут значення m_п відкладають по осі абсцис (Ох), значення — по осі ординат (Оу), значення H(Q) — по осі аплікат (Oz)). У свою чергу, для всіх відпо­відні критеріальні оцінки у тривимірному просторі утворювати­муть певну поверхню. Очевидно, що саме цій поверхні і належа­тиме критеріальна оцінка що відповідає вектору задачі Парето (7.56)—(7.61).

Отже, як бачимо, процес побудови множини ефективних портфелів пов'язаний із суттєвими труднощами, а тому безпосе­реднє використання згаданого означення не завжди може бути конструктивним. Спрощення у цьому плані можна досягнути введенням до розгляду портфелів, що визначаються на основі та­кої дефініції.

Портфель зі структурою називатимемо ефекти­вним згідно з концепцією Марковіца для будь-якого розподілу

ймовірності Q = (q₁,...,q_n), якщо всі допустимі вектори вигляду

є оптимальними за Парето для задачі (7.56)—(7.61).

Вимоги, наведені в цьому означенні, є досить жорсткими, але можна вказати випадок, коли існує портфель, що є ефективним згідно з концепцією Марковіца для будь-якого розподілу ймовір­ності, а визначення його структури зводиться до парної гри з ну­льовою сумою.

Розглянемо задачу створення портфеля активів як парну гру з нульовою сумою, що визначається матрицею R= (r_ij :і = 1,..., N; j = l,...,n), і нехай ця гра не має сідлової точки. Позначимо через Р^* = (p₁^*,...,p_n*) та Q^* =(q₁^*...q_n^* ) вектори, що відповідають оптима­льним змішаним стратегіям гравців, V* — ціна гри. Виявляється [123], що у випадку, коли мають місце строгі оцінки q₁^*>0, j = 1,...,n, портфель зі структурою X* =Р* (тобто х₁* = р_i^* , i = 1,...,N) є ефективним згідно з концепцією Марковіца для будь-якого розподілу ймовірності .

Зауваження. Звертаємо увагу на те, що строгі нерівності q_j > 0, j = l,...,n, можуть виконуватись лише в тому випадку, коли кількість активів є не меншою за кількість станів економічного середовища, тобто коли

Пошук портфеля, що є ефективним згідно з концепцією Мар­ковіца в полі інформаційної ситуації Ц, доцільно починати з оці­нки апріорних імовірностей qj станів економічного середовища (j = l,...,n). Ентропія Шеннона, що визначається формулою

досягає свого максимального значення при [123], тобто

(7.63)

Використовуючи знайдену точкову оцінку розподілу ймовір­ності станів економічного середовища в полі I₄, отримуємо то­чкові оцінки сподіваних норм прибутків активів:

(7.64)

їх дисперсій

(7.65)

а також коваріацій між нормами прибутків активів:

(7.66)

Очевидно, що оцінки коваріацій мають властивості, анало­гічні коваріаціям , а саме:

д„ = а,2; ди=ац; i = l,...,N; l = l,...,N.

Використовуючи оцінки (7.64)—(7.66) для пошуку ефектив­ного портфеля, приходимо до такої двокритеріальної оптиміза ційноїзадачі

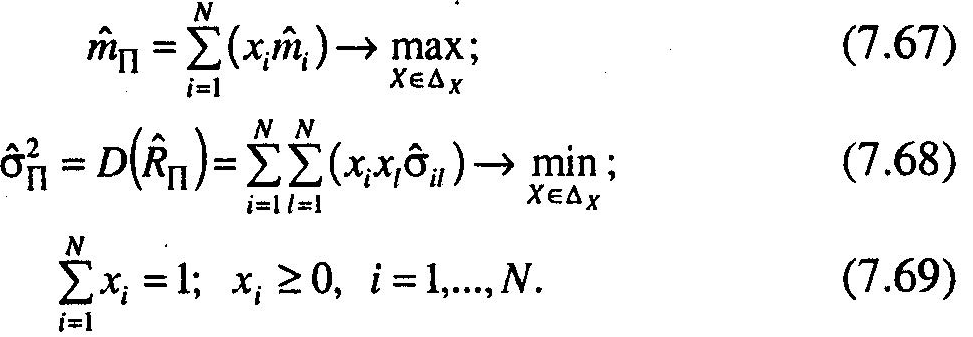
Розглянемо задачу створення портфеля активів у полі I₄ як парну фу з нульовою сумою, що не має сідлової точки, і нехай вектор X* = (x^*₁;...;x_n*) задає структуру ефективного портфеля в моделі Марковіца (7.67)—(7.69). Виявляється [123], що вектор є оптимальним за Парето для задачі (7.56)—(7.58).

У полі третьої інформаційної ситуації (Із) у разі, коли для ста­нів економічного середовища побудований ряд пріоритету і мають місце обмеження

(7.70)

або ж

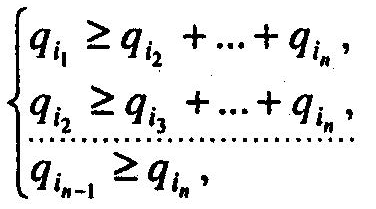(7.72)

або ж

(7.72)

для розрахунку точкової оцінки вектора розподілу Q можуть ви­користовуватись відповідні формули Фішберна [123]. Точкову оцінку вектора Q можна отримати також через відшукання мак-симума функції (7.58) при обмеженнях (7.60)—(7.61), до яких додаються обмеження (7.70) або (7.71), або (7.72). У полі її оцінка вектора Q визначається за критерієм

при виконанні умов (7.60)—(7.61), тобто здійснюється максимі-зація критерію (7.58) за сукупністю параметрів a) = (co,,...,coL), якими характеризується заданий відомий закон розподілу ймові­рності станів економічного середовища.

Трикритеріальну оптимізаційну задачу (7.56)—(7.61) можна звести до однокритеріальної, якщо при виконанні обмежень (7.59)—(7.61) ввести до розгляду критерій

де —нормалізовані критерії (7.56), (7.57) та (7.58) відповідно, — вагові коефіцієнти пріори­тету цих критеріїв, що задовольняють умовам

.

7.3.3. Теоретико-ігрова модель вибору структури портфеля у разі протидії економічного середовища

П'ята інформаційна ситуація (I₅) характеризується антагоніс­тичними інтересами економічного середовища щодо суб'єкта управління (інвестора) у процесі прийняття ним своїх рішень. Цей антагонізм досягається через вибір економічним середо­вищем таких своїх станів, які зводять до мінімуму ефективність інвестора. Тому основною стратегією для суб'єкта управління (інвестора) є забезпечення гарантованих рівнів економічних по­казників. Аналіз процесу прийняття рішень тут аналогічний ос­новним правилам та елементам теорії антагоністичних ігор. З урахуванням цього математична модель вибору структури порт­феля при виконанні обмежень (7.59)—(7.61) має вигляд:

(7 .73)

. .

(7.74)

(7.75)

де величини — функції змінних qv...,qn, що визначають­ся співвідношеннями (7.43), (7.44) та (7.45) відповідно.

Особливістю задачі вибору структури портфеля з критеріями (7.73)—(7.75) при виконанні умов (7.59)—(7.61) є те, що вона може мати єдиний «найкращий» розв'язок відносно всіх крите­ріїв. Тому й виникає питання щодо умов існування цього (єдино­го) розв'язку.

Розглянемо задачу створення портфеля активів у полі Is як па­рну гру з нульовою сумою, що визначається платіжною матри­цею , і нехай ця гра не має сідлової то­чки. Виявляється, що у разі, коли ця гра має єдиний розв'язок, множина G* усіх ефективних векторів задачі (7.73)—(7.75) за умов (7.59)—(7.61) має єдиний елемент

де — розподіли, що відповідають оптимальним змішаним стратегіям гравців.

Нехай у парній грі з нульовою сумою, що визначається матри­цею відсутня сідлова точка. Тоді, якщо ця гра має єдиний розв'язок, оптимальну змішану стратегію першо­го гравця, якій відповідає вектор називатимемо ефе­ктивним портфелем за концепцією Марковіца для п'ятої інформа­ційної ситуації {I₅), а вектор, який визначає оптимальну змішану стратегію другого гравця, — найбільш характерним розподілом імовірності щодо станів економічного середовища для I₅

Вибираючи за точкові оцінки апріорних імовірностей настан­ня станів економічного середовища відповідні компоненти q_j^* вектора Q*, що відповідає оптимальній змішаній стратегії друго­го гравця, дістаємо оцінки:

(7.76)

(7.77)

(7.78)

Якщо —структура допустимого портфеля, то отримуємо, що

(7.79)

чі=і У /=і ,=і

(7.80)

Якщо утворити портфель зі структурою то згі­дно з (7.79)—(7.80) маємо:

Де ціна гри — Дискретна випад­кова величина,що характеризує норму прибутку ефективного портфеля згідно з концепцією Марковіца для ситуації І5.

Нехай у парній грі з нульовою сумою, що визначається платі­жною матрицею відсутня сідлова точ­ка, і гра має кілька розв'язків. Тоді множина пар оптимальних змішаних стратегій гравців є нескінченною і при цьому для будь-якого елемента (Р*; Q*) цієї множини ціна гри залишається не­змінною, тобто

У такому разі як ефективний портфель згідно з концепцією Марковіца для ситуації I₅ можна використати будь-яку оптима­льну змішану стратегію першого гравця (для вказаної гри) з век­тором .

Зазначимо, що коли множина ефективних портфелів у моделі Марковіца у полі /5 має кілька елементів, тобто множина G* складається більше ніж з одного вектора, вибір портфеля, який би

найбільшою мірою задовольнив інвестора, здійснюється згідно з критерієм (7.80), а саме: вибирається той портфель, структура якого мінімізує дисперсію (для фіксова-нового розподілу станів економічного середовища Q*).

Розглянемо задачу створення портфеля активів у полі I₅ як парну гру з нульовою сумою, що визначається платіжною матри­ цею і нехай ця гра не має сідлової точ­ ки. Виявляється [123], що у разі, коли всі компоненти вектора Q* =(q_i^*,...,q^*_n) є строго більшими від нуля портфель, який визначається вектором є ефе­ктивним згідно з концепцією Марковіца для інформаційної ситу­ації I₅.