5.3.5. Аналіз ієрархій: теоретико-ігровий підхід

На даний час особливої ваги набувають системи, призначені для підтримки процесів прийняття рішень на всіх рівнях ієрархії соціально-економічних систем, зокрема дорадчі та експертні сис­теми. Назви цих систем повністю відповідають їхньому призна­ченню — «давати» на запит користувача поради щодо його пове­дінки у ризиковій ситуації, роблячи це на рівні досвідченого фахівця.

Психологічні аспекти використання методу аналізу ієрархії

Для побудови моделей управління та прийняття рішень необ­хідна інформація. Але наявної статистичної кількісної інформації як правило, буває обмаль. Досвіду теж ніколи не буває забагато. Основним джерелом інформації є люди (СПР, експерти, ко­ристувачі). Як правило, людині легше подати необхідні дані у неформалізованому вигляді або на вербальному рівні, на рівні якісного опису та оцінок (так звана м'яка інформація). Саме цим вимогам найбільшою мірою відповідає, зокрема, розроблений Т. Л. Сааті метод аналізу ієрархій (МАІ) [241, 242]. Його призна­чення — це підтримка прийняття багатоцільових багато критеріальних рішень при виборі одного з множини об'єктів (варіантів рішень, стратегій тощо).

Метод аналізу ієрархії (Analytic Hierarchy Process) є систе­матизованою математичною процедурою для ієрархічного по­дання елементів, які визначають сутність певної економічної проблеми. Метод полягає у декомпозиції проблеми на більш прості складові частини та подальшій обробці послідовності суджень СПР, що подаються у вигляді попарних порівнянь. Ці судження далі відображаються у кількісній формі. В результаті може бути виражений відносний ступінь (інтенсивність) взає­модії елементів в ієрархії.

МАІ включає також процедуру синтезу множинних суджень, отримання пріоритетності критеріїв і знаходження оптимальних (компромісних) рішень. МАІ знайшов уже багато практичних за­стосувань, зокрема реалізований у вигляді пакета прикладних програм (ППП) «Expert Choice».

Розв'язання економічної проблеми щодо вибору багатоці­льового багатокритеріального рішення (стратегії) розглядаєть­ся як процес поетапного встановлення пріоритетів цілей і кри­теріїв. Зазначимо, що людині притаманні дві ознаки аналітич­ного мислення [19]: перша — вміння спостерігати та аналізу­вати результати спостережень, друга — здатність встановлю­вати взаємозв'язки між спостереженнями, оцінюючи ступені щільності цих взаємозв'язків, а потім синтезувати ці взаємо­зв'язки у загальне сприйняття спостерігача. Зазначене дає уяв­лення про принцип ідентичності і декомпозиції, принципи дискримінації, порівняльного судження та синтезування, на яких і базується МАІ.

Принцип ідентичності та декомпозиції

Цей принцип передбачає структурування проблеми у вигляді ієрархії, що є першим етапом використання МАІ. Побудова ієрар­хії починається з накреслення відносно складної проблеми дослі­дження. У найпростішому вигляді ієрархія будується, починаючи з вершини в якій розміщується глобальна (узагальнена інтегро­вана) ціль, через проміжкові рівні (підцілі, чинники, критерії то­що) Д° найнижчого рівня, яким зазвичай є перелік альтернатив­ах рішень (стратегій).

Існує кілька видів ієрархій: найпростіші — домінантні, схожі на перекинуте дерево з основою (стовбуром) у вершині; холарії — домінантні «дерева» з оберненими зв'язками; модулярні ієрархії (китайські ящики) тощо. Подальший огляд обмежимо лише домі­нантними ієрархіями.

Домінантна ієрархія вважається повною, якщо кожен елемент заданого рівня функціонує як ціль (чи критерій) для усіх елемен­тів наступного, нижчого рівня. Існує кілька альтернативних спо­собів графічного зображення повної домінантної ієрархії. Два з них наведені на рис. 5.2 (там — елементи ієрархії, верхній ін­декс вказує на рівень ієрархії, нижній індекс — на їх порядковий номер на відповідному рівні ієрархії).

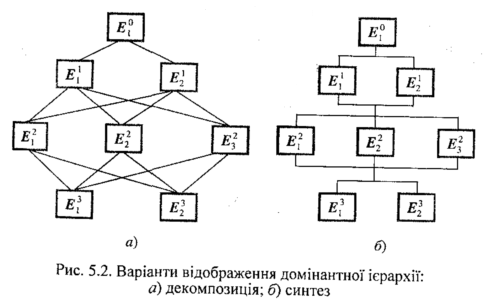
На рис. 5.2 варіант а) — конкретизація (декомпозиція) заданої множини елементів (цілей, критеріїв); варіант б) — протилежний першому і допускає синтез більш загальних елементів із заданих часткових.

При побудові домінантної ієрархії вважається, що виконується принцип ієрархічної неперервності, згідно з яким елементи нжчого рівня ієрархії є попарно порівняльними між собою з по­сяду елементів більш високого рівня. Цей процес неперервно продовжується від вершини ієрархії до її найнижчого рівня (аль­тернатив).

Зазначимо, що така форма низхідної декомпозиції може бути використана для розв'язування задач широкого класу. Можлива також модифікація з включенням петель оберненого зв'язку. Мають широке використання також домінантні ієрархії, в яких з різними критеріями (чи частковими цілями) пов'язані множини «альтернатив», що можуть різнитися як за складом, так і за кіль­кістю.

Цей етап МАІ потребує дискусій, у результаті яких вибира­ються множини цілей (чинників), критеріїв та альтернативних рішень (стратегій). Вибрані множини повинні відображати весь діапазон переваг і сприйняттів учасників (СПР, експертів і т. ін.), при цьому не є обов'язковою їх згода щодо всіх компо­нентів проблеми. Вирішальною є згода відносно вершини про­блеми.

Принцип дискримінації і порівняльних суджень

Наступним етапом після побудови ієрархії є порівняння між собою її елементів. Для цього формується метод порівняння. Найпоширенішим (з погляду практичного використання) є ме­тод попарних порівнянь, згідно з яким будується множина ма­триць попарних порівнянь. Для цього в ієрархії виокремлюють елементи двох типів: елементи-«батьки» та елементи-«на-щадки».

Матриці попарних порівнянь будуються для всіх елементів-«нащадків», що належать до відповідного «батьківського» еле­мента. Елементами-«батьками» можуть бути елементи, що нале­жать будь-якому ієрархічному рівню, крім останнього, де розмі­щені, як правило, альтернативні варіанти рішень (стратегій). Попарні порівняння здійснюються у термінах переваг (доміну­вання) одного елемента над іншим.

У загальному вигляді матриця попарних порівнянь формуєть­ся таким чином. Нехай — множина з елементів (альтернатив), що належать (і + 1)-му рівню ієрархії, — відповідно оцінки їх ваг (інтенсивності) з погляду «батьківсько­го» елемента Результати попарного порівняння елементів (і +1) -го рівня ієрархії подаються у вигляді матриці:

Якщо ваги (інтенсивності) елементів ієрархії попередньо неві­домі, то попарні порівняння здійснюються на основі суб'єктив­них суджень (СПР, експертів та ін.), що чисельно оцінюються за певною шкалою. Один з варіантів такої шкали наведено у табл, 5.1.

Правомірність використання цієї шкали нарівні з іншими до­ведено теоретично [241]. У тих випадках, коли важко вирізнити стільки проміжкових градацій від абсолютного до слабкого пріо­ритету або в цьому немає потреби у конкретній задачі, можуть використовуватись шкали з меншою кількістю градацій. Мініма­льна шкала може мати дві оцінки: 1 — елементи рівнозначні;

2 — пріоритет одного елемента щодо іншого. Матриця у такому

разі заповнюється цілими (відмінними від нуля) числами та обе­рненими до них (дробами). Очевидно, що для побудови матриці СПР (експерт) здійснює —-

попарних порівнянь (тут — порядок матриці).

Під час проведення попарних порівнянь необхідно дати відпо­відь на такі запитання: 1) який з двох порівнюваних елементів є важливішим і чи має він більший вплив; 2) реалізація якого з двох порівнюваних елементів є імовірнішою і якому з них нада­ється перевага? Для порівняння критеріїв (або часткових цілей) зазвичай запитують, який (яка) з них важливіший; для порівнян­ня альтернативних рішень (стратегій) відносно «батьківського» елемента — якому з альтернативних рішень надається перевага або яке з них є імовірнішим?

МАІ однаковою мірою охоплює чинники, що піддаються чи не піддаються вимірюванню і тоді для них вимагаються вербаль­ні судження.

Методом попарного порівняння альтернатив не завжди можна ефективно скористатись в деяких практичних ситуаціях:

• експерту можуть запропонувати для аналізу понад дев'ять альтернатив. У такому випадку побудова однорідних матриць попарних порівнянь ускладнюється. Це пов'язано з фізичними обмеженнями інтелекту людини;

• альтернативи можуть надходити до експерта для порівняння не одночасно, а через певні проміжки часу. В цій ситуації немож­ливо попарно порівняти об'єкти тощо.

У наведених і деяких інших ситуаціях для порівняння (а також оцінювання) альтернатив доцільно скористатись методом порівнян­ня альтернатив відносно стандартів або методом копіювання [12].

Принцип синтезування

Після побудови ієрархічної моделі і складення матриці попарних порівнянь надходить черга наступного етапу МАІ — ієрархічного синтезу. Сутність цього етапу полягає у побудові вектора рейтингових оцінок альтернативних рішень (стратегій) через синтез векторів пріоритету матриць попарних порівнянь часткових цілей, критеріїв тощо. Вектори пріоритету щодо елементів певного рівня ієрархії, які попарно порівнюються між собою (рядки матриць попарних по­рівнянь), можна обчислити такими способами:

• як головний власний вектор матриці;

• як середньо геометричне елементів рядків матриці (окремо для кожного рядка);

• іншими методами.

Якщо скористатись методом, що наводиться у [123, розд. 5], то отримана оцінка головного власного вектора Wj матриці по­парних порівнянь може використовуватись як вагові коефіці­єнти пріоритету щодо елементів (i + 1)-го рівня ієрархії з погляду «батьківського» елемента ієрархії , тобто

Якщо ж за елементи вектора пріоритету використовувати середньо геометричні елементів рядків матриці , тобто величини

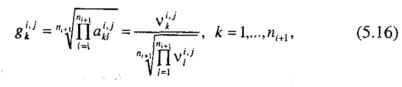
За оцінку узгодженості суджень експерта у розрізі матриці попарних порівнянь використовується індекс:

де — індекс узгодженості суджень, — максимальне власне значення матриці попарних порівнянь [123, розд. 5].

Можна показати [241, 242], що за та за індекс ІУС = 0.

У разі, коли безпосереднє обчислення величини [123, розд. 5] спричиняє певні труднощі, можна скористатись набли­женим методом [19], що складається з двох послідовних кроків.

Крок 1. Для кожного стовпчика матриці попарних порівнянь обчислюється сума його елементів:

із цих сум утворюється вектор-рядок:

Крок 2. Величина покладається рівною добутку векторів тобто

Використовується також відносна оцінка узгодженості су­джень:

де ВУСij — відносна узгодженість суджень експерта у розрізі ма­триці попарних порівнянь Aij; ІУСij — індекс узгодженості су­джень у розрізі матриці Aij; М(ІУС) — нормативне значення (ма­тематичне сподівання) індекса узгодженості суджень, обчислен­ня якого здійснюється експериментально, через імітаційне моде­лювання матриці попарних порівнянь. У табл. 5.2 наведені зна­чення М(ІУС) залежно від порядку матриці (отримані в [241]).

Таблиця 5.2

НОРМАТИВНІ ЗНАЧЕННЯ ІНДЕКСА УЗГОДЖЕНОСТІ СУДЖЕНЬ

Порядок матриці, п	Нормативне значення,М(ІУС)	Порядок матриці,п	Нормативне значення, М(ІУС)	Порядок матриці, п	Нормативне значення,М(ІУС)
1 2 3 4 5	0,00 0,00 0,58 0,90 1,12	6 7 8 9 10	1,24 1,32 1,41 1,45 1,49	11 12 13 14 15	1,51 1,54 1,56 1,57 1,59

Як допустиме використовується значення ВУСдоп <0,1 (у де­яких випадках використовується ВУСдоп < 0,2). Якщо ж для мат­риці попарних порівнянь ВУСij перевищує задану норму (0,1 чи 0,2), то це вказує на те, що заповнення матриці попарних порі­внянь здійснювалось із суттєвими порушеннями щодо логічності суджень. Тому експертові пропонується перевірити свої суджен­ня, а то й заново структурувати задачу.

Враховуючи, що за пi+1 = 2 індекс узгодженості суджень lYCij = 0, нормативне значення індекса узгодженості суджень М(ІУС) = 0, отримуємо, що ВУСij= 0/0, тобто є невизначеним. Для уникнення невизначеності в цьому випадку (за пi+1 = 2) при­ймають ВУСij = 0.

Оцінка узгодженості ієрархії

Оцінювання узгодженості всієї ієрархії здійснюється складан­ням зважених показників узгодженості всіх її рівнів [12].

Якщо для матриць , що відповідають елементам Eji i-ro рі­ вня ієрархії , визначено індекси узгодженості

суджень і з цих індексів утворено вектори-рядки

і'о індекс узгодженості повної домінантної ієрархії (ІУІ) (що має L. рівнів) визначається за формулою:

Узгодженість ієрархії можна оцінювати також і на основі від носної оцінки:

ВУІ = ІУІ/М(ІУІ),

де ВУІ — відносна узгодженість ієрархії, М(ІУІ) — нормативне значення індексу узгодженості ієрархії. Для повної домінантної ієрархії А/(ІУІ) обчислюється за формулою:

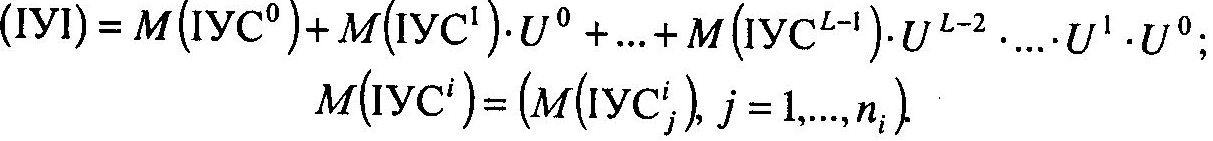
Узгодженість ієрархії вважається допустимою, якщо ВУІ < 0,1 (іноді допускається ВУІ < 0,2).

Урахування (суджень) кількох експертів

Для підвищення ступеня об'єктивності та якості процедури прийняття рішення доцільно враховувати думки кожного з екс­пертів, що входять в експертну раду. Розрахунок агрегованої оці­нки у випадку залучення до експертної ради Т експертів, які ма­ють різну компетентність (кваліфікацію), здійснюється за фор­мулою:

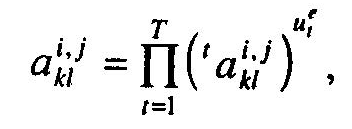
де — результат порівняння t-м експертом елементів — «на­щадків» відносно «батьківського» елемента — ваговий коефіцієнт пріоритету (компетентності) експерта, що входить у раду

Обчислити коефіцієнти компетентності експертів можна на основі інформації, яку містять вектори вагових коефіцієнтів:

(вектор iUij розраховується на основі аналізу матриці попарних

порівнянь iAij, яка заповнена на підставі суджень t-ro експерта,

t = l,...,T). Інформацію, яку містять вектори iUij, зведемо у табл. 5.3.

Таблиця 5.3

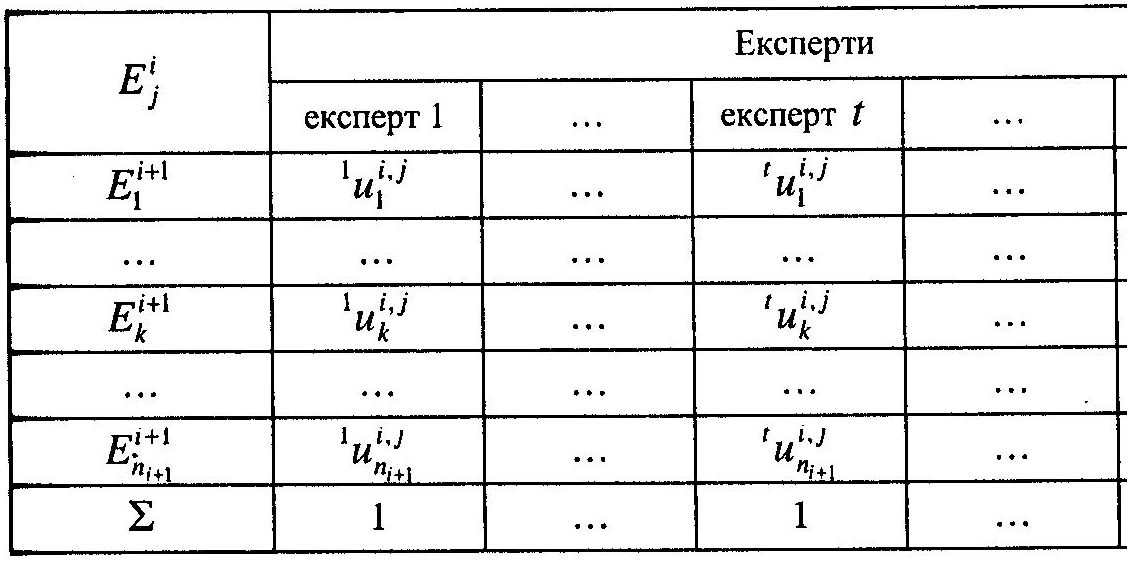
Алгоритм обчислення коефіцієнтів компетентності експертів має вигляд рекурентної процедури [83]:

Обчислення починають для 5=1, вибираючи при цьому за по­чаткові наближення значень коефіцієнтів компетентності вели­чини:

Тоді групові оцінки вагових коефіцієнтів пріоритету об'єктів (елементів (i + 1)-го рівня ієрархії) першого наближення дорів­нюють середнім арифметичним значенням оцінок експертів:

Далі обчислюється:

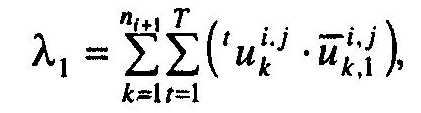
а також перші наближення щодо значень коефіцієнтів компетен­тності експертів (перша ітерація):

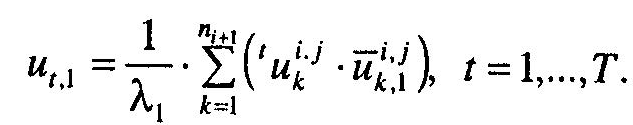
Використовуючи перші наближення коефіцієнтів компетент­ності, можна повторити весь процес обчислень і дістати другі на­ближення (друга ітерація) . На s-й ітерації отримує­мо оцінки. . Якщо на (s + l) ітерації дістанемо, що

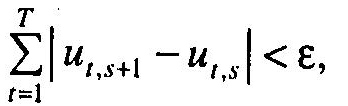
(де є>0 задається наперед), то вважатимемо, що подальші обчи­слення (ітерації) не дають істотного уточнення. Отже, оцінки век­тора коефіцієнтів експертів стабілізувались, а тому можна вважа­ти, що

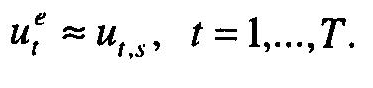
Зауваження 5.3. До роботи в експертній раді можуть залуча­тись фахівці, різні за професією (наприклад, управлінці, маркето-логи, аналітики та ін.) та кваліфікацією. На якість інформації (що її містять матриці попарних порівнянь) впливає міра компетент­ності експертів щодо аналізованої проблеми (елементи (і + 1)-го рівня ієрархії, і критерію (елементи Eij), відносно

якого здійснюється цей аналіз. Тому оцінку вектора компетент­ності експертів (і на його основі — урахування їхніх думок) не­обхідно здійснювати щоразу після побудови ними відповідних матриць попарних порівнянь.

5.4. НЕЧІТКА БАГАТОКРИТЕРІАЛЬНА ІЄРАРХІЧНА МОДЕЛЬ ПІДТРИМКИ ПРИЙНЯТТЯ РІШЕНЬ

Як зазначалося вище, майже кожна більш-менш складна еко­номічна задача прийняття рішення (індивідуального і тим паче колективного) є задачею прийняття рішень в умовах ризику за наявності багатьох критеріїв.

Задача оцінки скінченної множини варіантів (стратегій) і век­торної оптимізації пов'язана з невизначеністю при спробі вияви­ти взаємну (відносну) важливість різних аспектів (критеріїв) що­до прийняття рішень. У [136] подано аналіз різних нечітких моделей, які можуть бути використані в експертних і дорадчих

системах і які доцільно застосовувати в умовах неповноти, неод­нозначності, недовизначеності, розпливчастості вихідної інфор­мації та зумовленого цим ризику. При побудові нечітких моделей важливу роль відіграють лінгвістичні змінні. З їх допомогою за певними правилами можна формалізувати (девербалізувати) які­сну інформацію стосовно об'єкта прийняття рішень, представле­ну у вербальній (словесній) формі фахівцями-експертами, вико­ристовуючи розпливчасті (нечіткі) множини.

У наукових публікаціях щодо прийняття рішень сполучення те­рмінів «багатокритеріальний» і «нечіткий» зустрічаються досить часто. Однак, як зазначається зокрема в [136], більшість авторів, сформулювавши на початку аналізу задачу прийняття рішень як не­чітку та багатокритеріальну, вже на першому ж кроці її розв'язання (дослідження) використовують певну згортку критеріїв і надалі ви­вчають скалярну нечітку задачу прийняття рішень. Згортки, як пра­вило, вводяться інтуїтивно, на підставі здорового глузду, залежно від змісту конкретної задачі, раціональних суджень тощо.

У [51, 76, 78] запропонований дещо інший підхід — модифіка­ція методу АНР (Analytic Hierarchy Process), розробленого Т. Л. Сааті для підтримки прийняття рішень при багатокритеріальному ви­борі одного з множини об'єктів (варіантів), який ще називають методом аналізу ієрархій (МАІ) (див. 5.3.5.1). У літературі описані алгоритми (різні його модифікації1), які для подолання браку кі­лькісних даних використовують інформацію (оцінки), отриману на підставі спеціально прийнятих і використовуваних штучних шкал оцінювання [122, 341, 355]. Втім, як підкреслюється зокрема в [355], застосування такого підходу, що будується на описовому характері даних, не завжди дає бажані результати.

Запропонована в [51, 85] та наведена далі модифікація МАІ полягає у використанні понятійного і математичного апаратів те­орії нечітких (розпливчастих) множин, який вперше був запро­понований у працях Л. А. Заде [137, 353]. Завдяки цьому стає можливим безпосереднє оперування різного роду вербальними (лінгвістичними) даними.

У ряді праць, зокрема в [181], розглядається поняття нечіткої (розпливчастої) множини. Нехай X — довільна непуста множина. Нечіткою підмножиною множини X називається множина пар

(5.18)

Функція називається функцією належності до

нечіткої множини , аХ— базовою множиною чи базовою шка-

лою. Для кожного конкретного значення х є X величина набуває певного значення із замкненого інтервалу [0; 1], що на­зивається ступенем належності елемента я: до нечіткої множини . Носієм нечіткої множини називається підмножина А множи­ни X, яка містить лише ті елементи множини X, в яких значення функції належності є більшими від нуля.

Функції належності однієї й тієї ж множини можуть бути різ­ними при визначенні їх як різними людьми, так і однією люди­ною залежно від настрою останньої, схильності до ризику, від мети побудови нечіткої підмножини, розв'язуваної задачі, обра­ної конкретної методики побудови тощо.

Лінгвістична змінна [137,181] характеризується набором , в якому — назва лінгвістичної змінної; — терм-множина лінгвістичної змінної (3, тобто множина лінгвістичних (ве­рбальних) значень змінної, кожне з яких є нечіткою змінною з обла­стю визначення X; G — синтаксичне правило (має звичайну форму граматики), породжує назви (імена) вербальних значень лін­гвістичної змінної ; М — семантичне правило, яке ставить у від­повідність кожній нечіткій змінній нечітку множину — зміст нечіткої змінної . Для спрощення запису формул по­значають множину як , а множину як Т, коли йдеться про певні нечіткі змінні і лінгвістичні змінні . Окрім цього, вико­ристовують спрощене визначення лінгвістичної змінної як трійки ( , Т, X), вкладаючи у позначення те саме розуміння, що й вище.

Підкреслимо, що лінгвістичною змінною є змінна, яка задана на деякій шкалі і приймає значення, що є словами та словосполу­ками природної чи штучної мов. Значення лінгвістичної змінної описуються нечіткими (розпливчастими) множинами.

Ступінь належності елементів х до нечіткої множини інтерпретується, зокрема в [181], як суб'єктивна міра того, наскіль­ки елемент* є Xвідповідає поняттю, сутність якого формалізується нечіткою множиною. Під суб'єктивною мірою розуміють, як прави­ло, визначений опитуванням експертів ступінь відповідності елеме­нта х є X поняттю, яке формалізується нечіткою множиною.

Існує два класи методів побудови функції належності нечіткої (розпливчастої) множини — прямі та опосередковані. Найпрос­тіше функція належності нечіткої множини, що відповідає зна­ченню лінгвістичної змінної . будується за прямими методами для одного експерта. При побудові експерт кожному елементу множини X ставить у відповідність певний ступінь належності

, який, на його погляд, найкращим чином узгоджується зі

змістовним навантаженням (інтерпретацією) множини . Відпо­відність між ступенями належності з інтервалу [0; 1] та елемен­тами х множини X може бути задана у вигляді таблиці, прикладу, графіка, формули, що задає аналітичну форму функції належнос­ті нечіткої множини

Опосередковані методи ґрунтуються на «обережнішому» ви­користанні особи як вимірювального приладу. Найбільш застосо­вуваним з цієї групи є метод попарних порівнянь. Розглянемо йо­го сутність.

Функція належності визначається, зокрема, за матрицею

попарних порівнянь , елементи якої тij являють собою деякі оцінки інтенсивності належності елементів хi є X до нечіт­кої множини у порівнянні з елементами хj є X . Якщо припус­тити, що значення функції належності відомі для всіх xi є X , наприклад, , то попарні порівняння можна представити квадратною матрицею відношень Якщо відношення точні, то маємо співвідношення:

де п — власне значення матриці М, знаючи яке, можна відшукати вектор r (з урахуванням умови — вектор-стовпчик, транспонований до r.

У [340] показано, що в загальному випадку емпіричний вектор повинен задовольняти задачу знаходження власного значення матриці М, де — найбільше власне значення. Задача зво­диться до знаходження власного вектора г, який задовольняє рівнянню:

(5.19)

Оскільки відомо, що це рівняння має єдиний розв'язок, то значення координат власного вектора r, який відповідає макси­мальному власному значенню (Хтах), поділені на їх суму, будуть шуканими ступенями належності.

Щодо одержання матриці попарних порівнянь, то вона буду­ється таким чином (див. 270—273). Проводиться опитування експерта відносно того, наскільки, на його думку, елемент xi є більш значущий для поняття, що описується нечіткою множи­ною, ніж елемент xj. Поняття, якими може оперувати експерт, та

детерміністична інтерпретація цих понять відповідними величи­нами mij наведені у табл. 5.1. На підставі даних таблиці для під­вищення узгодженості оцінок вважається, що , звідки тij =1 — для діагональних елементів і — для елементів, симетричних відносно головної діагоналі.

Припустимо, що опитування експертів проведено на детермі­ністських засадах бездоганно і матриця попарних порівнянь по­будована абсолютно точно. Тоді матриця М має такий вигляд:

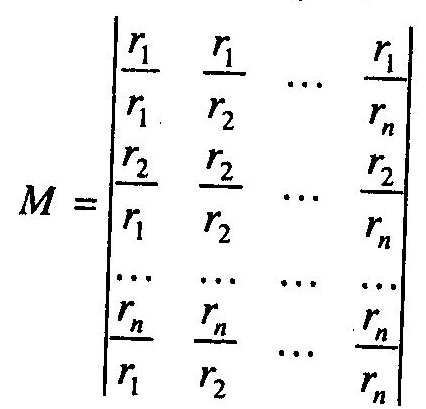
У такому разі для визначення j-го елемента вектора r можна скористатися такою процедурою. Обчислимо суму елементів j-го стовпчика матриці М. Нехай ця сума є деяке число кj , тобто:

(5.20)

Одержимо, що

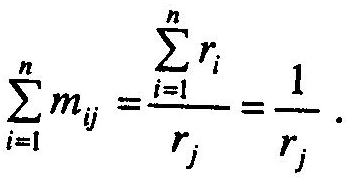
Таким чином, .

Здійснюючи процедуру, аналогічну попередній, по всіх стовп­чиках матриці М, будуємо шуканий вектор r.

Тепер припустимо, що, як це часто має місце, матриця попар­них порівнянь побудована неточно. Тоді описану процедуру що­до визначення вектора r можна використати для визначення лише його початкового наближеного значення в ітераційному процесі розв'язку рівняння (5.19). При цьому відхилення від п може бути використане для оцінки точності розв'язку системи рівнянь на певному кроці ітераційного методу.

У [29] сформульовано ряд додаткових умов, яким повинні за­довольняти функції належності нечітких множин, що описують терми лінгвістичних змінних.

Запропонований у [51, 85] алгоритм є однією з модифікацій МАІ і складається з п'яти основних кроків. їх черговість і спектр основних операцій на кожному кроці узгоджується із загальною методикою МАІ, враховуючи, звичайно, вербальний характер вихідних даних.

Один із способів використання якісних (вербальних) оцінок та пов'язаних з ними нечітких множин наводиться у табл. 5.4.

Таблиця 5.4

Інтенсивність	Якісна оцінка	Позначення якісної оцінки	Нечітка множина з відповідною якісною оцінкою
1	ОднаковЬ важливо	ОВ	{(1,0/1)}
3	Ненабагато важливіше	НВ	{(0,5/1), (0,75/2), (1,0/3), (0,75 /4), (0,5 /5)}
5	Суттєво важливіше	СВ	{(0,5/3), (0,75/4), (1,0/5), (0,75 /6), (0,5 /7)}
7	Значно важливіше	ЗВ	{(0,5/5), (0,75/6), (1,0/7), (0,75/8), (0,5/9)}
10	Абсолютно важливіше	АВ	{(0,5/9), (1,0/10)}

Отже, маємо такі основні кроки:

Крок 1. Формування багаторівневої ієрархічної структури, яка містить інтегрований критерій, часткові критерії та об'єкти (про­екти, стратегії) досліджування та впорядкування (вибору).

Крок 2. Побудова матриць попарних порівнянь з нечіткими оцінками для елементів, які знаходяться на окремих рівнях ієрархії.

Крок 3. Обчислення значень вагових коефіцієнтів (векторів пріо­ритетів) , кожного з елементів ієрархічної структури з погляду елемента, який перебуває на безпосередньо вищому рівні ієрархії.

Крок 4. Обчислення вектора пріоритетів , який визначає не­чіткі оцінки аналізованих об'єктів (проектів, стратегій) з по­гляду інтегрованого критерію.

Крок 5. Впорядкування досліджуваних об'єктів (проектів) відносно величини нечітких оцінок .

Опишемо сутність операцій, здійснюваних на окремих кроках пропонованого алгоритму.

І. (Крок 1). Формування багаторівневої ієрархічної структури критеріїв. Загальний вигляд ієрархічної багатокритеріальної струк­тури зображено на рис. 5.3. На верхньому рівні цієї структури (рі­вень 0) знаходиться лише один елемент — інтегрований критерій оцінювання, який можна розкласти (деталізувати) на кілька елемен­тів (часткових критеріїв), тобто рівень 1, що йде безпосередньо за даним рівнем ієрархії. Кожний елемент цього рівня ієрархії, в свою чергу, деталізується на кілька елементів наступного рівня і т. д. На найнижчому рівні ієрархічної структури перебувають стратегії (об'єкти, проекти), які необхідно аналізувати та впорядковувати чи обирати один з них (елементи досліджуваної множини).

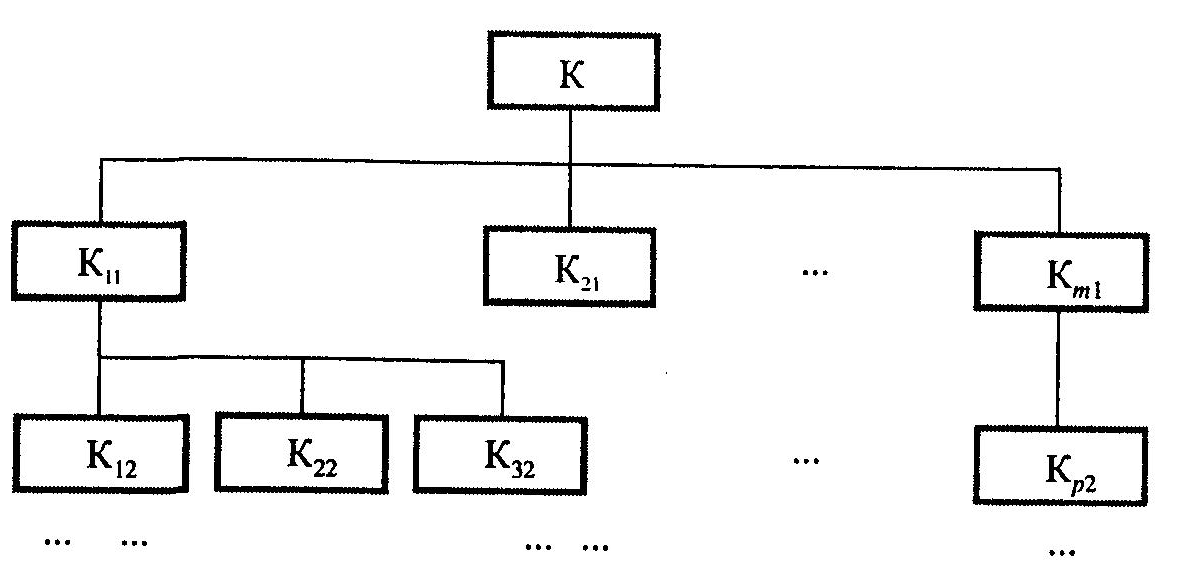
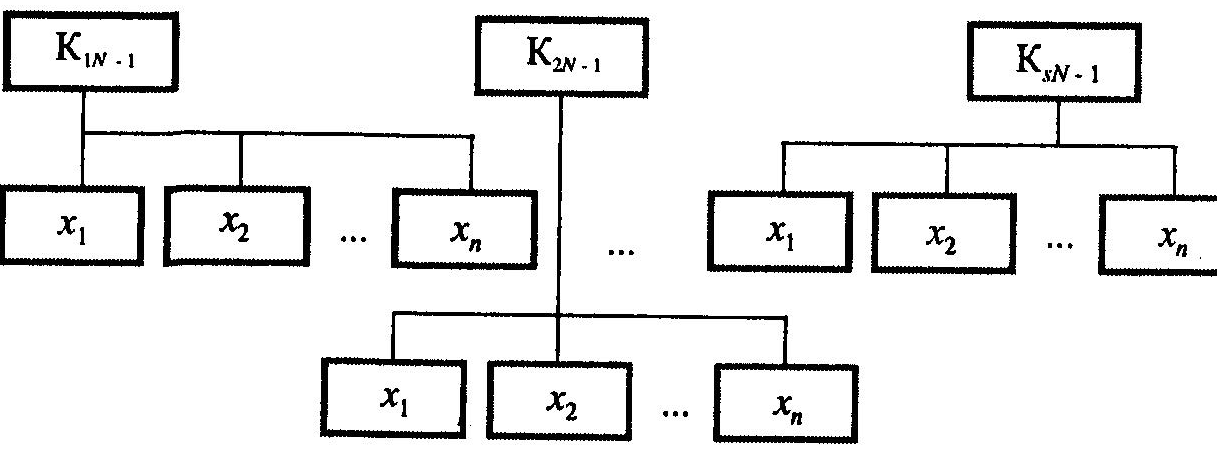
Рис. 5.3. Загальний вигляд багаторівневої ієрархічної структури

Побудована в такий спосіб ієрархічна багаторівнева структура дозволяє обмежитися відносно невеликою кількістю елементів на кожному рівні ієрархії та подолати проблеми, спричинені склад­ністю інтегрованого критерію (як зазначалося в [341, 342]), що розглядається в багатьох випадках як критерій згортки.

2. (Крок 2). Побудова матриці попарних порівнянь елементів з нечіткими оцінками.

Для аналізу критеріїв оцінювання, що містяться на певних рі­внях ієрархічної структури, пропонується побудова матриці по­парних порівнянь елементів у вигляді:

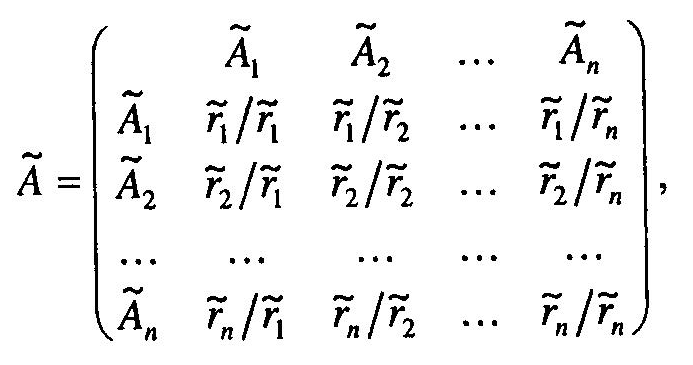
де —нечіткі порівнювані елементи; —нечі­ткі вагові коефіцієнти (пріоритети) порівнюваних елементів; п — кількість порівнюваних елементів.

Побудовані у такий спосіб матриці порівнянь дають можли­вість здійснити попарне порівняння елементів на певному рівні ієрархічної структури з погляду їх важливості щодо критерію, який знаходиться на безпосередньо вищому рівні ієрархії і який є, власне, їх агрегованим критерієм (згорткою). При аналізі чис­лових критеріїв (заданих на відповідних числових шкалах) можна обчислити окремі вагові коефіцієнти ri; та їх взаємне попарне відношення у вигляді числових величин.

Враховуючи нестачу (відсутність) кількісних даних щодо оці­нки відношення пропонується відійти від при­йнятого в МАІ детермінованого підходу введенням та застосу­ванням лінгвістичного підходу, який ґрунтується на теорії розпливчастих (нечітких) множин [29, 181, 341]. Для того, щоб одержати наведену вище нечітку матрицю попарних порівнянь, проводять опитування експерта відносно того, наскільки, на його думку, хi є вагомішим (значущим) для поняття, яке описується нечіткою множиною , ніж елемент xj. У табл. 5.4 наводяться поняття (лінгвістичні змінні), якими оперує експерт, інтерпрета­ція цих понять — нечіткі (розпливчасті) множини , що

можна представити одним з можливих переходів від вербального опису до нечіткого (девербалізації).

Визначення нечітких множин (девербалізація), які репрезен­тують використовувані значення лінгвістичної змінної, досяга­ється експертизою. Техніка визначення функції належності для нечітких (розпливчастих) множин наводиться, зокрема, в [181]. За допомогою цієї техніки стає можливим визначення нечіткої множини, що відповідає введеним термам лінгвістичної змінної. Після цього можна здійснювати необхідні логічні та алгебраїчні операції з нечіткими множинами [3, 29, 138, 181].

Отже, матриця попарних порівнянь (використовувана в МАІ) може бути модифікованою. Замість числових попарних відно­шень вводяться вербальні (розпливчасті) відношення . Тут символом «~» (тильда) позначено нечіткі кате­горії, тобто такі, які визначаються за допомогою нечітких мно­жин. Маючи вербальні оцінки, можна сконструювати низку роз­пливчастих матриць попарних порівнянь.

Для ієрархічної структури, представленої на рис. 5.3, це: на першому рівні — одна матриця для порівняння часткових крите­ріїв на другому рівні — т матриць для порівнян­ня часткових критеріїв ,. з погляду кожного з т кри­теріїв першого рівня, на рівні N — s матриць для порівняння п об'єктів з погляду кожного з критеріїв безпосередньо вищого рі­вня, тобто рівня (N-1).

3. (Крок 3). Обчислення векторів нечітких ваг елементів ієрар­хічної структури.

Для наведеної на рис. 5.3 ієрархічної структури знаходимо, наприклад, вагові коефіцієнти критеріїв з погляду інтегрованого критерію К або критеріїв з погляду, наприклад, критерію К11 тощо. Маючи на меті знаходження цих вагових коефіцієнтів застосовується техніка середньої геомет­ричної для нечіткої множини [321]. Знаходження вагових коефі­цієнтів полягає в обчисленні середньої геометричної , для еле­ментів матриці у такий спосіб:

(5.21)

а також знаходженні нормалізованих нечітких вагових коефіцієнтів

(5.22)

Вони утворюють для кожної матриці порівнянь певний розпливчастий вектор пріоритетів .

4. (Крок 4). Обчислення (розпливчастого) вектора пріоритетів об'єктів (проектів) найнижчого рівня з погляду інтегрованого критерію (нульового рівня).

Вектор пріоритетів , який визначає оцінки дослі­джуваних об'єктів хі,...,хп з погляду інтегрованого критерію К, згідно з методикою МАІ можна одержати множенням матриць, Стовпчиками яких є вектори пріоритетів ряду поруч розташова­них рівнів ієрархічної структури, відповідно з їх зв'язками, вка­заними нарис. 5.3.

Нехай розглядається деякий l-й рівень ієрархічної структури, елементи якого перебувають на безпосередньо вищому рівні що­до елементів рівня l + 1, і одночасно вони знаходяться на один рі­вень нижче, ніж елементи рівня l-1.

Нехай маємо:

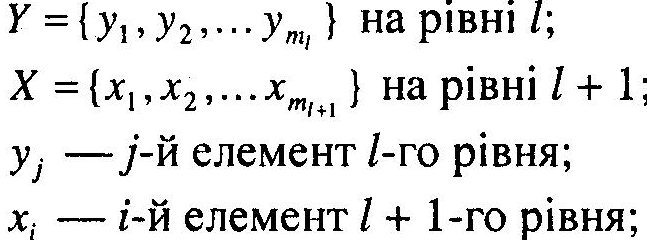
z — елемент рівня l- 1, якому безпосередньо підпорядковані всі елементи множини Y.

Нехай на рівні l - 1 маємо певну функцію пріоритетів для відповідних елементів з рівня l:

на рівні / маємо функцію пріоритетів для елементів l+1 рівня, які підпорядковані окремим елементам 1-го рівня:

.

Отже, з погляду відповідних елементів рівня l - 1 розпливчасті вагові оцінки рівня l + 1 можна подати за такою формулою:

Якщо позначити через матрицю з елементами , то маємо для трирівневої ієрархічної структури

згідно з [321] — вектор-стовпчик пріоритетів, що

складається з елементів — вектор-стовпчик пріорите­тів, що складається з елементів

Користуючись методом математичної індукції, одержимо для N-рівневої ієрархічної структури, зображеної на рис. 5.3, вектор пріоритетів елементів найнижчого (N-ro) рівня з погляду елемен­та (інтегрованого критерію К) найвищого рівня ієрархічної стру­ктури (0) у вигляді:

(5.23)

де вектор-стовпчик репрезентує розпливчасті вагові оцінки аналізованих об'єктів з погляду інтегрованого кри­терію (К); — вектор-стовпчик розпливчастих вагових коефіці­єнтів елементів рівня 1 з погляду інтегрованого критерію (К); — матриці, вектор-стовпчиками яких є розпливчас­ті вектори пріоритетів відповідних елементів певного l-го рівня з погляду елемента безпосередньо вищого рівня (l - 1) ієрархічної структури (з урахуванням їх зв'язків, зазначених на рис. 5.3).

5. (Крок 5). Впорядкування досліджуваних об'єктів щодо ве­личини нечітких оцінок .

Після реалізації третього і четвертого кроків алгоритму маємо оцінки , що являють собою розпливчасті коефіцієн­ти аналізованих об'єктів з погляду інтегрованого критерію К. На даному кроці необхідно порівняти між собою для впорядкування об'єктів х1,...,хn відповідно до величин цих оцінок. Але, оскільки одержані оцінки є лише нечіткими (роз­пливчастими) множинами, то впорядкування об'єктів не є очеви­дним.

Таке впорядкування не можна виконати коректно, якщо спи­ратися лише на максимальні величини носіїв нечітких множин або лише на ті величини носіїв, яким відповідають максима­льні ступені належності. Впорядкування лише відносно максима­льних значень носіїв нечіткої множини не завжди призводить до коректного результату, бо великі значення носіїв можуть висту­пати з малими ступенями належності, і навпаки. Впорядкування лише на підставі тих значень носіїв, які мають максимальний ступінь належності, теж не завжди дає добрий результат, бо при цьому не враховуються всі інші елементи носія без урахування їх величин і відповідних їм значень функції належності. Умовою правильного впорядкування об'єктів є врахування як величин но­сіїв, так і їх ступеня належності у нечітких множинах .

Для цього в модифікованому алгоритмі доцільно використати, зокрема, концепцію максимізуючої множини за Иєном [321]. Максимізуючою множиною є така нечітка множина:

де

Т— множина всіх носіїв, які представляють розпливчасті оцінки аналізованих об'єктів .

Ступінь належності в максимізуючій множині визначає ступінь близькості кожної величини носія до максимальної вели­чини носія у множині Т, тобто в множині всіх носіїв нечітких множин , які представляють оцінки об'єктів, що аналізуються з погляду інтегрованого критерію.

У межах кроку 5 виконуються такі етапи:

1. утворення максимізуючої множини;

2. формування для кожного об'єкта х1,х2,...хn розпливчастої множини , яка є модифікованою оцінкою , тобто

(5.26)

де

(5.27)

— оператор мінімума, що відповідає логічній операції «/»;

3) формування нечіткої множини — такої, що

(5.28)

де

(5.29)

v — оператор максимуму (логічне «або»), застосування якого приво­дить до того, що кожен об'єкт порівнюватиметься з іншими на під­ставі максимального ступеня належності в множині

У рамках даного етапу залежно від прийнятої системи гіпотез можливі різні модифікації. Зокрема, враховуючи ентропію як міру невизначеності, формування нечіткої множини можна виконати, якщо замість (5.29) скористатися таким виразом:

Для цього кожну з розпливчастих множин розподілимо на груп. Подібне групування слушно здійснити, зокре­ма, за принципом близькості у кожній розпливчастій підмножині відповідних значень носіїв.

Тобто, якщо Тут — задане число.

Приймаючи для кожної множини

одержимо

де

4) формування нечіткої множини через відносну нормалі­зацію елементів нечіткої множини :

де

(5.31)

5) впорядкування досліджуваних об'єктів (проектів) за величиною ступеня належності у множині (від бі­льшого значення серед до меншого).

Зауважимо, що отримані таким чином результати обчислень справедливі лише в рамках досліджуваної групи об'єктів (проек­тів, стратегій). За величиною ступеня належності в нечіткій мно­жині можна обрати серед досліджуваних об'єктів той, для якого , а решту розташувати відповідно до спадання вели­чини функції належності .

Перевагою наведеного підходу є те, що за його допомогою відносно неважко проаналізувати причини отримання тих чи ін­ших оцінок, використовуючи сформовану на кроці 1 ієрархічну структуру (див. рис. 5.3), аналізуючи (змінюючи), у разі необхід­ності, відповідні матриці якісних («м'яких») попарних порівнянь, верифікуючи вихідні судження.

Наведений алгоритм, який названо «розпливчастим методом аналізу ієрархій» (РМАІ), — ефективний при розв'язуванні проблем Прийняття рішень з урахуванням ризику, які вимагають багатовимір­них (багатокритеріальних) порівнянь, та коли складно чи немож­ливо одержати необхідні кількісні дані або процес здобуття кількіс­них даних потребує багато часу і зусиль, коштів, а натомість є мож­ливість відносно просто дістати вербальні (описові) дані.

Не останньою перевагою РМАІ є можливість представлення вербальних даних у вигляді, зручному для комп'ютерної обробки інформації в системах підтримки прийняття рішень, обтяжених ризиком. Алгоритм зручний для створення інтерактивної інфор­маційної системи багатокритеріального аналізу за відсутності кі­лькісної інформації, що дозволяє залучити кінцевого користувача (суб'єкта прийняття рішень) безпосередньо до процесу оціню­вання варіантів, верифікації вербальних («м'яких») оцінок тощо.

РМАІ допускає ряд модифікацій залежно від прийнятої раціо­нальної системи гіпотез, різних, адекватних ситуації, правил пе­реходу від лінгвістичного опису альтернатив до розпливчастого (девербалізації) тощо.