5.3.3. Критерій мінімальної відстані між інформаційними кубами

Нехай різні (в тому числі і суперечливі) цілі СПР відобража­ються N функціоналами оцінювання

Для спрощення викладок вважатимемо, що всі матриці F¹ (l = l,...,N) за фіксованої кількості рядків (рівній т) мають одна­кову кількість стовпчиків, тобто:

Мається на увазі, що побудова кожного функціонала оціню­вання відбувається на основі рівних щодо кількості, але не збіж­них поелементно множин станів економічного середовища . У випадку, коли функціонали оціню­вання будуються на основі однієї і тієї ж множини станів економічного середовища, розподіли ймовірності настання цих станів для кожного з них можуть бути різними.

Нехай аналітиками ідентифіковані інформаційні ситуації, в полі яких необхідно приймати рішення, а також визначені лока­льні критерії якості стратегій, що відповідають цим інформацій­ним ситуаціям. Тоді, як це запропоновано у [123], для кожного цільового функціонала оцінювання F¹ будуємо куб інформації елеме­нтами якого є оцінки чистих стратегій Sk для кожного стану еконо­мічного середовища згідно з t-м критерієм якості на основі функ­ціонала оцінювання F¹. Для чистої стратегії s_k через вертикальний перетин кубів інформації К', l=1, ..., N отримуємо N інформацій­них матриць K'(s_k), які, у свою чергу, об'єднуємо в куб інформації щодо стратегії. Цей куб позначимо через KK(s_k), k = l, ..., m.

Для змішаної стратегії s_P куб інформації будуємо за формулою:

3 урахуванням пріоритету функціоналів оцінювання, що задаєть­ся вектором вагових коефіцієнтів U^F =( l= 1,...,N), застосовуючи методику Хеммінга, визначимо відстань між кубами інформації стосовно чистої стратегії Sk І змішаної стратегії sp за формулою:

Де U^1E =( ,l=1,…,n)— вектор вагових коефіцієнтів пріоритету за врахування як пріоритету інформаційних ситуацій, так і пріо­ритету локальних критеріїв якості стратегій [123].

Тоді математична модель принципу оптимальності для бага­тоцільової багатокритеріальної задачі має вигляд:

Якщо ж для оцінювання відстані між кубами інформації вра­ховуються лише несприятливі для СПР відхилення, то принцип оптимальності набуде вигляду:

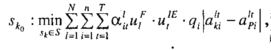
де - індикатор несприятливого відхилення.

5.3.4. Ієрархічна модель прийняття багатоцільових багатокритеріальних рішень

В основу ієрархічної моделі прийняття багатоцільових багато­критеріальних рішень покладено принцип гнучкого (одночасно­го) врахування пріоритету локальних критеріїв якості стратегій, інформаційних ситуацій (у полі яких застосовуються ці критерії) та функціоналів оцінювання (що адекватно відображають цілі, яких хоче досягнути СПР). Розглянемо задачу знаходження багатоцільового багатокритеріального рішення (стратегії), коли СПР виокремлені N цілей і кожній з них відповідає свій функціонал оцінювання. Функціона­ли оцінювання можуть мати різні інгредієнти, різну розмірність ^То.Щ°- Рішення приймається комплексно, тобто виходячи з позиції різних інформаційних ситуацій. Крім того, в полі кожної ін­формаційної ситуації рішення повинне враховувати особливості Різних критеріїв прийняття рішень.

Для розв'язання поставленої задачі доцільно скористатись Ієрархічною моделлю, структуру якої наведено на рис 5.1.

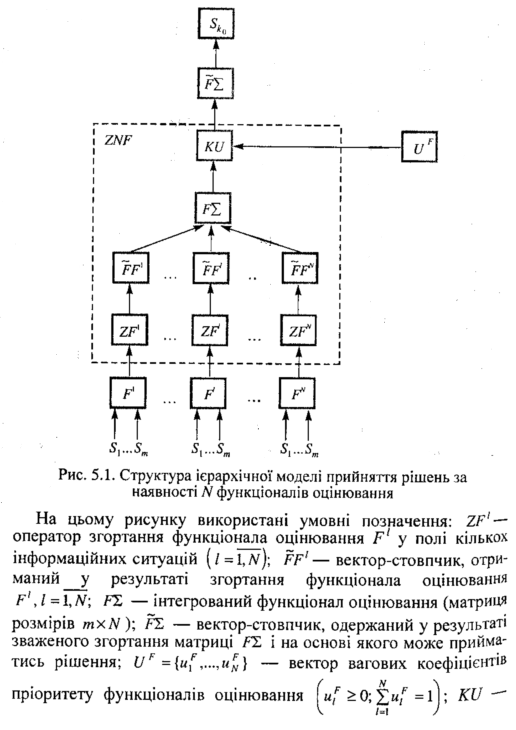
оператор зваженого згортання з урахуванням вектора вагових ко­ефіцієнтів пріоритету.

Якщо позначити через ZNF оператор згортання N цільових функціоналів оцінювання в полі кількох інформаційних ситуацій, то структуру відповідної ієрархічної моделі підтримки прийняття рішення можна подати у вигляді такої схеми:

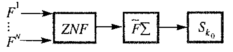
Логічним є подальше узагальнення наведеної моделі. Зокрема, у випадку прийняття рішень, процеси опрацювання яких є розпарале-леними і здійснюються кількома «штабними» командами (напри­клад, Організація Об'єднаних Націй, Євросоюз, корпорації, побудо­вані на принципах організаційної ієрархії (холдингу), урахування глобального, регіонального (територіального) поділів тощо). У та­кому разі може виникнути необхідність у порівнянні інформації, яку містять вектори-стовпчики виду «FT» — рейтинги відповідних рішень (проектів) з позиції нації - держави або кожного структурного підрозділу (чи «штабної» команди). Тому доцільно у разі виникнен­ня подібної ситуації ввести ще один рівень ієрархії — рівень прези­дента корпорації (генеральної дирекції фірми тощо).

Перспективним є використання запропонованого підходу до побудови ієрархічних моделей, що враховують динаміку розвит­ку економічної системи.