4.3. Узгодження та агрегування оцінок експертів з урахуванням компетентності

Залучення до експертизи кількох експертів з подальшою агре­гацією їхніх оцінок широко використовується для підвищення достовірності експертних оцінок (ЕО) і рішень, які приймаються на базі цього. Методи агрегації суттєво залежать від типу ЕО, ко­трі визначаються завданнями експертизи. Експертні оцінки-числа використовуються у вирішенні багатьох практичних задач.

Для агрегації результатів ранжування методом попарного по­рівняння альтернатив кількома експертами за шкалою «більше», «менше», «рівнозначно», як зазначалося вище, можна використо­вувати метод відшукання матриці порівнянь (медіани Кемені), котра має мінімальну сумарну відстань до матриць, які описують дані експертами ранжування. У низці наукових праць вирішена та сама задача з урахуванням компетентності експертів.

Узагальненішим є завдання визначення кардинальних оцінок, тобто числових характеристик значущості альтернатив стосовно деякого критерію. Останнім часом підвищилась актуальність та­кої області застосування методів вирішення цієї задачі, як систе­ми підтримки прийняття рішень, в яких використовуються Ієрар­хії критеріїв методом Саатi чи ієрархії цілей, і експерти залучаються до визначення пріоритетів або коефіцієнтів значу­щості критеріїв, цілей і альтернатив.

У працях американського вченого Т. Л. Сааті запропоновано як агреговану оцінку коефіцієнта відносної значущості критерію (альтернативи) використовувати середнє геометричне вказаних коефіцієнтів, обчислених за матрицями попарних порівнянь, да­ними кількома експертами. У низці наукових праць запропоно­вано метод визначення коефіцієнта узгодженості (КУ) з ураху­ванням компетенції експертів, що є кількісною оцінкою рівня узгодженості множини ЕО, і використання цієї Інформації для агрегації оцінок, одержаних методом безпосереднього оціню­вання. Розроблено також метод кількісної оцінки рівня внутрі­шньої узгодженості результатів попарних порівнянь, виконува­них кількома експертами, з урахуванням компетенції, а також визначення достатньої узгодженості для встановлення агрегова-ної оцінки.

Для знаходження агрегованої оцінки результатів попарних порівнянь, виконуваних кількома експертами, обчислення КУ необхідне, але недостатнє. Дійсно, що робити, коли узгодженість ЕО недостатня? Метод Дельфі передбачає у такому разі ознайом­лення експерта з усередненою і граничною оцінками. Однак, як­що експерти виконують попарні порівняння, то навіть коли екс­перт хоче змінити свої оцінки, щоб поліпшити їх узгодженість з оцінками інших експертів, йому досить важко визначити, що і в якому напрямі він повинен змінювати. Розроблено методи попа­рних порівнянь, які передбачають діалог з експертом, пропону­ються варіанти зміни його оцінок, спрямовані на поліпшення внутрішньої узгодженості результатів попарних порівнянь і при­ймаються його відповіді про згоду чи незгоду прийняти той чи інший варіант , У праці В. Г. Тоценка пропонується поширити даний підхід на діалоги з кількома експертами, під час яких ви­значаються пропозиції тому чи іншому експерту про напрям ко­ригування його оцінок для досягнення достатнього рівня узгод­женості результатів попарних порівнянь, виконуваних даними експертами. Також враховується компетентність експертів.

Задача групового оцінювання пріоритетності альтернатив сто­совно критерію К формулюється так. Нехай наявні множина експертів множина альтернатив і s-й експерт (s = l,...,d) характеризується нормованим відносним коефіцієнтом компетентності с_s. Задано також алгоритм визна­чення кожним експертом ненормованих ЕО , i = 1,...,m важли­вості альтернатив стосовно критерія К (у подальшому скорочено — «ваг»). Необхідно знайти агреговані узгоджені нормовані оцінки и>,- відносної пріоритетності альтернатив.

Визначимо більш строго поняття «агреговані» й «узгоджені» оцінки. Не втрачаючи загальності, вважатимемо, що ЕО . є пев­ною позицією деякої шкали з п поділками. Якщо ,- представле­на дійсним числом (одержаним, наприклад, внаслідок обробки матриці попарних порівнянь (МПП)), то, обравши допустиму по­милку , не складно перейти до задання цієї оцінки у вигляді но­мера поділки шкали з є поділками. Тип шкали визнача­ється алгоритмами одержання й обробки ЕО. Передбачається, що шкала є шкалою відношень, інтервалів, різниць чи абсолютною, бо саме в шкалах названого типу представляються ненормовані значення показників відносної пріоритетності альтернатив, оде­ржані використанням відомих І пропонованих методів.

Множину , де - оцінка ваги альтернативи , пода­на s-м експертом, зручно задавати спектром R_v.

Означення 1, Спектром R_v множини V ЕО, представлених у шкалі з п поділками, називається «позиційний вектор, на j-й позиції якого записано значення експертних оцінок, заокругле­них до j -ї поділки шкали.

Визначаючи агреговані оцінки з урахуванням компетентності експертів, множину V будемо задавати зваженим спектром

Означення 2. Зваженим спектром S_v множини V ЕО, пред­ставлених у шкалі з n поділками, називається n - позиційний век­тор, на j-й позиції якого записана сума коефіцієнтів компетент­ності експертів, оцінки яких заокруглені до j-ї поділки шкали.

Означення 3. Узгодженими агрегованими відносними оцінка­ ми wi, i = 1 т важливості альтернатив відносно критерію К

називаються нормовані, коректно обчислені середні достатньо узгоджених множин ненормованих оцінок важливості, даних d експертами.

Коректність обчислення середнього визначається відповідніс­тю операції знаходження середнього типу шкали, в якій предста­влені ЕО. Для шкал названих типів допустимою операцією ви­значення середнього є операція обчислення середнього арифметичного.

Зважений спектр S_v множини V оцінок експертів вважається достатньо узгодженим, якщо його КУ перевищує деякий поріг застосування. Для кількісної оцінки ступеня узгодженості спект­ра S_v використовуватимемо спектральний КУ, що визначається виразом

де d — кількість експертів; q — кількість груп експертів, які да­ли однакові оцінки; j(l) — номер поділки шкали, до якого заок­руглені оцінки, дані експертами l-ї групи, 1 = 1, ...,q; — су­ма коефіцієнтів компетентності експертів, оцінки яких заокруглені до поділки з номером j(l); z — булєва функція, ко­тра задає необхідні і достатні умови рівності нулю КУ k(S_v). Із (4.28), (4.29) випливає, що КУ приймає значення в межах [0; 1],

причому повністю узгодженій множині ЕО відповідає значення 1, а найменш узгодженій — 0.

Для визначення достатності рівня узгодженості спектра S_v використовуються значення порога виявлення Т₀ і порога засто­сування Т_и.

Означення 4. Порогом виявлення Т₀ називається коефіцієнт узгодженості множини ЕО, яка містить мінімальну реєстровану кількість інформації.

Означення 5. Порогом застосування Т_и називається КУ мно­жини ЕО, що забезпечує обчислення агрегованої ЕО з допусти­мою точністю.

Поріг застосування Т_и дорівнює КУ k(S_u) зваженого спектра

S„, в якому d = 2,

Розглянемо метод узгодження та агрегації ЕО відносної пріоритетності альтернатив, одержаних методом безпосередньої оцінки.

При використанні цього методу кожний з d експертів дає не­ залежну ненормовану оцінку v_is і-й альтернативі, i = 1, ..., m, i = i,...,m, s = l d , причому оцінки, дані 5-м експертом, знахо­ дяться в межах qs_min -q_smax. У загальному випадку з s k випли­ває, що . Тому виникає необхідність пе­рерахунку оцінок альтернатив у шкалах з різними границями до єдиної шкали, що має зазвичай найбільшу кількість поділок. Оці­нку v_is на шкалі з границями подамо через оцінку v_ik з границямі

Коефіціенти перерахунку та зміщення, дорівнюють

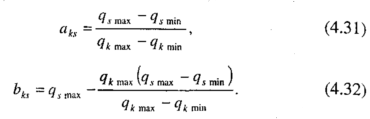
Після зведення оцінок альтернатив до єдиної шкали з використанням (4.30)—(4.32) будуються спектри ваги кожної альтерна­тиви. До спектра Si i-ї альтернативи включаються оцінки v_і1, v_і2, ..., v_id> які дав їй кожен експерт. Після цього відповідно до (4.28) обчислюються коефіцієнти узгодженості спектрів ваг альтернатив, а також поріг виявлення Т₀ і поріг застосування Т_и.

Множина спектрів поділяється на три множини, що не пере­тинаються. До підмножини включаються спектри, для яких

Виконання умови (4.33) означає, що спектри не містять інформації. При цьому експертам пропонується переглянути свої оцінки тих альтернатив, спектри ваг яких задовольняють даній умові, для чого за рішенням керівника можуть бути організовані консультації експертів.

Стосовно спектрів підмножини можна стверджувати, що кожний з них містить інформацію, але ступінь її узгодженості недостатній для визначення агрегованої оцінки з достатньою то­чністю. Тому для підвищення узгодженості таких спектрів можна провести діалог з експертами. Процедура організації діалога сто­совно кожного спектра аналогічна і полягає в такому. Обчислю­ється середня оцінка ваги альтернативи. Оскільки при викорис­танні методу безпосереднього оцінювання ваги альтернативи представлені в абсолютній шкалі, за умови рівної компетентності експертів середня оцінка v_d дорівнює середньому арифметичному компонент спектра, що надані різними експертами. Якщо екс­перти мають різну компетентність, то

Далі визначається експерт е_j, для якого в розглядуваному спектрі , величина максимальна. Вказаному експерту пропонується переглянути свою оцінку v_lf альтернативи А_l в напрямі зменшення Д . Якщо експерт згоден, то його оцінка змі­нюється так, щоб у спектрі S_l компонента v_lf змістилась у бік середнього на одну поділку шкали, в якій представлені ЕО. Після цього знову розраховуються КУ приведеного спектра S_l і вико­нується описаний вище аналіз, за необхідності з подальшим зве­рненням до експерта. Якщо експерт e_f відмовився коригувати

оцінку v_lf , то він виключається з множини E_s експертів, до яких

можна звертатися з пропозицією змінити оцінку ваги альтернати­ви A_t на подальших кроках. Вказаним вище методом визначаєть­ся експерт е_р, якому відповідає наступне за величиною відхи­лення А, після чого відбувається аналогічний діалог уже з цим експертом. Якщо на деякому кроці виявилось, що і одно­часно Т₀ k(Sj)<T_u, то це означає: можливості поліпшення узго­дженості вичерпані, незважаючи на її недостатність. У такому разі робиться висновок про необхідність зміни складу команди експертів.

Виконання описаних процедур підвищення узгодженості при­зводить або до того, що на деякому кроці спектри ваг усіх альтер­натив належать підмножині , або до висновку про неможливість одержати достатньо узгоджені оцінки від цієї команди експертів. Належність спектра підмножині означає, що він достатньо уз­годжений, і тому за ним можна знайти узагальнену оцінку ваги альтернативи, що дорівнює середньому значенню, знайденому за виразом (4.36). На завершальному етапі нормують значення v_i І одержують коефіцієнти w_i. відносної пріоритетності альтернатив

4.4 ВИЯВЛЕННЯ ТА УЗГОДЖЕННЯ ПЕРЕВАГ .