3.4. Граничні межі ризику

Слід зазначити, що дисперсія (варіація) як міра ризику непов­ністю характеризує ступінь ризику, але дозволяє в низці випадків з притаманною точністю виявити граничні можливості інвестора або підприємця. Теоретичною основою цього є лема Маркова та нерівність Чебишева. Лема Маркова проголошує: якщо випадко­ва величина X не набуває від'ємних значень, то для будь-якого додатного числа є справедливою буде нерівність:

де М(X) — математичне сподівання випадкової величини X. Нерівність Чебишева стверджує: ймовірність того, що випад­кова величина відхиляється за модулем від свого математичного сподівання більше, ніж на заданий допуск , не перевищує її дис­персії (варіації), поділеної на , тобто

де М(Х) — математичне сподівання випадкової величини X; — середньоквадратичне відхилення випадкової величини.

Ця нерівність містить важливу інформацію, якщо

Припустимо, що інвестиції здійснюються за рахунок кредиту, взятого під відсоток під заставу нерухомості [210]. Яка ймовір­ність того, що інвестор не зможе повернути свій борг і позбу­деться своєї нерухомості? Це ймовірність того, що випадкова ве­личина Х набуде значення, яке відповідає умові:

Звідси маємо, що шанс збанкрутувати не перевищує величини

Звичайно при цьому мають на увазі, що обов'язково викону­ється умова раціональності такого вкладу «під кредит»: , а оцінка (3.25) має сенс лише тоді, коли варіація (дисперсія) не надто велика, тобто

При заданих умовах (гіпотезах), щоб шанс збанкрутувати був би не більшим, ніж 1/9( , достатньо виконати умову (пра­вило «трьох сигм»)

Зазначимо, що тут як один з параметрів ризику у системі його кількісних оцінок виступає ймовірність несприятливої події

поряд з таким параметром ризику, як дисперсія (варіація). У даному випадку приймається, що р_н<1/9. Звичайно, можна сперечатися, чи задовольняє ця величина менеджера (суб'єкт прийняття рішення), чи ні. У ряді випадків величину необхідно брати досить малою інколи (навіть у разі забезпечення «допустимого» ризику) = 0,001. У загальному випадку необ­хідно приймати додаткові гіпотези, використовувати методи інтелектуальної підтримки прийняття рішень тощо.

Зазначимо, що для більшості економічних показників неспри­ятливою подією логічно вважати відхилення в несприятливу сто­рону від обраної бази. Так, якщо X відображає прибуток чи ін­ший показник економічного ефекту, то жоден суб'єкт гос­подарювання не заперечуватиме проти його зростання. Не­сприятливими подіями у такому разі будуть лише ті, за яких зна­чення показника ефекту виявиться меншим за значення встанов­леної бази. В таких випадках, як зазначається у [124], ефек­тивнішим (з погляду точності оцінки) є застосування нерівності Кантеллі.

Нехай досліджується економічний показник X, який тракту­ється як випадкова величина. Відомі такі параметри цієї випадко­вої величини: т — математичне сподівання; а — середньоквадратичне відхилення. Нехай нормативно задається також величина L — встановлений рівень економічного ефекту, недосягнення якого трактується як несприятлива подія. Нерівність Кантеллі полягає у встановленні ймовірності несприятливої події, яка оці­нюється за формулою:

Необхідно також наголосити на діалектичній об'єктивно-суб'єктивній оцінці ризику, що має місце в оцінці Кантеллі. Як­що параметри т та о мають об'єктивний характер, то поняття «несприятлива подія» і «ризик» чисельно характеризуються встановленням допустимого рівня порогового (бажаного) зна­чення випадкової величини (X > L) який є суб'єктивним і зале­жить від суб'єкта ризику.

Імовірність як один з показників міри ризику широко викори­стовується у «Safety first» при моделюванні задач вибору оптимального портфеля на ринку акцій. Норма доходу (R) звичайної акції може бути представлена як випадкова величина зі статисти­чно оціненими характеристиками (використовуючи дані минулих періодів). Зрозуміло, що й норма доходу портфеля з кількох акцій також буде випадковою величиною. Позначимо через норму

доходу деякого портфеля k з сукупності портфелів К, обраних інвестором до розгляду; т_к — середня норма доходу портфеля к; — середньоквадратичне відхилення портфеля к. Нехай Rі встановлений інвестором (бажаний) пороговий рівень норми до­ходу портфеля, а значення , нижче за цей рівень, нехай буде несприятливою подією. Відомі три основні критерії типу «Safety first», котрі наводяться у деяких працях [314]:

1. критерій Роя. Оптимальним вважається портфель із сукуп­ності К, який дає мінімальне значення ймовірності як ступеня ри­зику P(R_к< );

2. критерій Катаока. Оптимальним портфелем із сукупності К вважається портфель, який дає максимальне значення 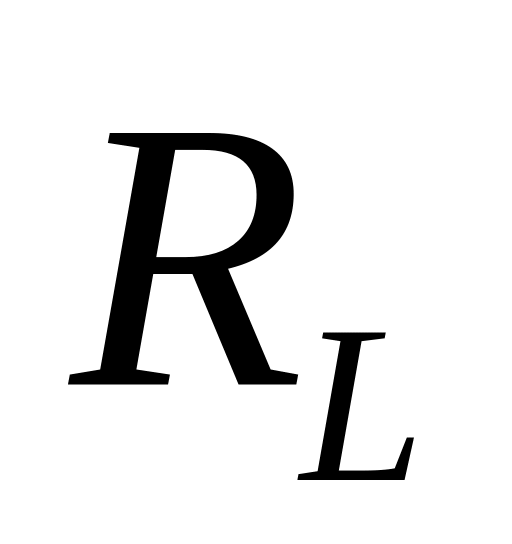за умови

де — встановлений інвестором ступінь ризику;

3. критерій Телсера. Оптимальним із сукупності портфелей К вважається такий портфель, який дає максимальне значення ма­ тематичного сподівання 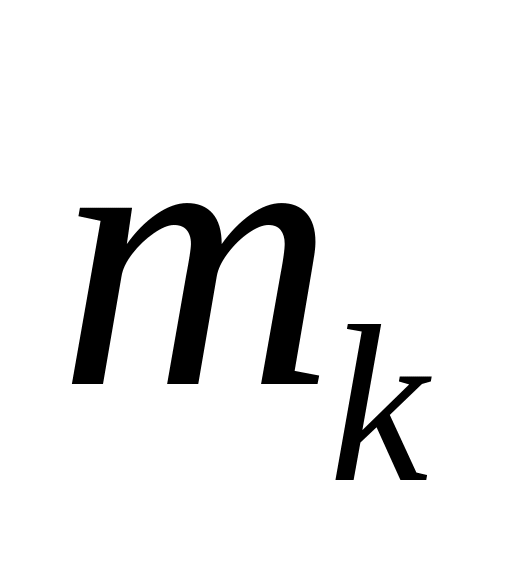за умови, що

де — встановлений Інвестором ступінь ризику.

Очевидно, що для оцінки ймовірностей у кожному з наведе­них критеріїв можна використати нерівність Кантеллі.

Існує ціла система показників кількісної оцінки ступеня ризи­ку. Але, як зазначається у низці праць [52, 294], від жодного кіль­кісного показника ступеня ризику не слід очікувати, що він пока­зуватиме адекватні результати за будь-яких обставин. Тобто встановлення певного єдиного показника як кількісної міри (сту­пеня) ризику є спробою подолати невизначеність, характеризую­чи випадкову величину (ефективність, збитки) одним (єдиним) показником (числом). На нашу думку, кількісна оцінка ризику є багатовимірною величиною (вектором): , компонен­ти якої , формуються залежно від мети дослідження, прийнятої системи гіпотез, суб'єктивного чинника, який характе­ризує ставлення суб'єкта ризику (управлінської команди) до не­визначеності та ризику тощо.

У загальній теорії ризику досить часто вводять деякі числа В, які характеризують, зокрема, ефективність проекту за допомогою співввідношення [210]:

де R — випадкова величина, яка характеризує ефективність чи збитки досліджуваної економічної системи (об'єкта); M [ ] — оператор математичного сподівання; U(R) — та чи інша аналіти­чна функція, яку називають функцією корисності. Так, якщо U(R) = R, то В = т(R), де т(R) — математичне сподівання випад­кової величини К. Тобто стохастика (випадковість) тут спрощено характеризується лише сподіваним значенням випадкової вели­чини R (як правило, це можливі збитки). Якщо ж

де R — випадкова величина значення економічної ефективності; U(R) — функція корисності певного суб'єкта прийняття рішення (управлінської команди); k — задане число (параметр); D(R) — дисперсія випадкової величини R, яка характеризує її розсіюван­ня щодо математичного сподівання т(К). У багатьох працях приймається, що

де ) — середньоквадратичне відхилення. Тобто спо­дівана корисність ураховує як сподіване значення, так і варіацію випадкової величини.

Зупинимось на деяких питаннях, що стосуються кількісної оцінки та врахування ризику, і є актуальними у фінансово-економічних проблемах прийняття рішень, обтяжених ризиком.

Ще одним показником ступеня ризику, який визначає суб'єк­тивне ставлення до нього особи, яка приймає рішення, є рівень значущості . Вибір величини залежить від низки чинників, зо­крема схильності, несхильності, байдужості до ризику його суб'єкта, від величини наявного капіталу тощо.

За заданим рівнем значущості (ризику) а можна знайти k = к(а) таке, що

Тобто існує к, що з імовірністю не меншою, ніж чи з ризиком не більшим, ніж , можна стверджувати, що

Узагальнюючи викладене, можна стверджувати, що, врахову­ючи міру ризику та ставлення до нього суб'єктів прийняття рі­шення, оцінюють так зване ефективне значення (В) відповідного економічного показника. Вважатимемо, що суб'єкти прийняття рішень несхильні до ризику. Якщо досліджуваний показник має позитивний інгредієнт, тобто його прагнуть максимізувати, то його ефективне значення (В⁺) обчислюється за формулою:

де М[R] — математичне сподівання випадкової величини К; k — певний постійний коефіцієнт (ціна ризику); — середньоква­дратичне відхилення (міра ризику). Якщо ж досліджуваний пока­зник має від'ємний інгредієнт, тобто його прагнуть мінімізувати, то його ефективне значення ( ) обчислюється за формулою:

При визначенні ефективних значень В⁺ та за ступінь ризику обрано вектор ), компонентами якого є . Зрозуміло, що це — спрощений підхід до оцінки та врахування невизначеності і породженого нею ризику.

У подальшому розглядатимуться випадки, коли досліджува­ний показник має додатний інгредієнт. У низці випадків буває заданим певне значення Rо — нормативне значення показника ефективності проекту, тобто йдеться про те, що ефективне зна­чення В⁺ показника ефективності R обов'язково має дорівнювати чи перевищувати величину заданого нормативного значення, тобто В⁺ > Rо. Інакше такий проект нас не влаштовує і відхиля­ється. Якщо з урахуванням ступеня ризику прийняти ефективне значення показника якості проекту за певний вираз від т(R), , зокрема,

то в цьому випадку можна дійти висновків щодо прийняття прое­кту, порівнюючи значення Rо та В⁺.

Якщо одним із показників ступеня ризику обрати величину семіквадратичного відхилення (SSV(R)), можна отримати нерів­ності, аналогічні нерівностям (3.31), (3.32).

Введемо випадкову величину

Покладемо у лемі Маркова , отримаємо

З нерівності (3.35) випливає, що з імовірністю, не меншою і ніж , можна стверджувати, що

Враховуючи, що для будь-якого дійсного х: викону­ється рівність , отримаємо

А отже, з імовірністю, не меншою ніж у, виконуватиметься нерівність

Тобто ризик порушення останньої нерівності буде не більшим, ніж а.

Якщо з урахуванням ризику прийняти ефективну оцінку пока­зника ефективності проекту рівною

то, порівнюючи зі значенням R₀, можна дійти висновків щодо прийняття чи відхилення проекту.

Однак слід наголосити, що у низці випадків математичне спо­дівання не є ні єдиною, ні адекватною характеристикою випадко­вої величини R, і тому його доцільно було б замінити, наприклад, модою. Моду можна визначити як значення випадкової величини R, що найчастіше зустрічається в наборі вибіркових даних дослі­джуваного показника. Тобто це — найтиповіше значення серед вибіркових даних і часто його слід вважати репрезентативнішим, ніж математичне сподівання. Наприклад, у маркетингу мода ви­користовується для вивчення попиту населення на товари споживання (одяг, взуття), коли дослідника цікавить розмір, котрий ко­ристується найбільшим попитом, тощо.

Зрозуміло, що оцінки значень математичного сподівання, мо­ди, медіани збігаються для симетричних розподілів випадкових величин. Але у більшості випадків розподіли економічних показ­ників асиметричні і тому за базу доцільно обирати моду, а у низці випадків — медіану. Наприклад, розподіл заробітної плати серед працівників певного підприємства (фірми) чи у регіоні, розподіл доходів тощо характеризуються асиметричними розподілами.

На нашу думку, обирати за базу модальне значення (М_а) де­якої дискретної випадкової величини R, яка набуває значень з імовірностями, відповідно рівними p є сенс тоді, коли ймовірність р_к цього значення Rk =М₀ суттєво домінує порівняно з іншими значеннями імовірностей цієї випад­кової величини, тобто коли , де — задане експертним шляхом значення, або якщо

У такому разі за ефективне очікуване значення відповідного еко­номічного показника (R), на нашу думку [54], доцільно обирати мо-у, скориговану на величину, пропорційну ступеню ризику, а за міру ризику — модальне семіквадратичне відхилення SSV_М0 (див. п. 3.2).

Нехай для випадкової величини R (показника ефективності певного проекту) відомі значення моди (М₀), середньоквадратичного відхилення від моди ( ), семіквадратичного відхилення в

несприятливу сторону від моди (SSV_Мо ). Скористаємось знову лемою Маркова для

Отже, для заданого рівня надійності (або рівня значущості ) iснує k таке, що

Звідси маємо, що з імовірністю, не меншою ніж , виконується нерівність

Тобто, можна оцінити ефективне значення показника якості проекту (R), приймаючи за показник ступеня ризику величину :

Для семіквадратичного відхилення у несприятливу сторону від моди можна отримати аналогічну нерівність:

Отже, для заданого рівня надійності (або рівня значущості ) знайдеться k таке, що

і при цьому ризик порушення останньої нерівності буде не біль­шим, ніж .

Якщо прийняти за міру ризику величину , отримаємо таку оцінку ефективного значення показника якості проекту:

Порівнявши оцінки зі значенням можна схвалю­вати проект чи відхиляти його.

У низці випадків за базу доцільно обирати медіану як най адекватнішу характеристику досліджуваного показника, а за ефекти­вне значення цього економічного показника R — медіану, скориговану на величину, пропорційну відповідному показникові ступеня економічного ризику.

Нехай для випадкової величини R (показника ефективності певного проекту) відомі значення медіани (М_е), середньоквадра­тичного відхилення від медіани ( ), семіквадратичного відхи­лення у несприятливу сторону від медіани ( ).

Скористаємось лемою Маркова для

Отже, для заданого рівня надійності (або рівня значущості ) існує k таке, що

Звідси маємо, що з імовірністю, не меншою ніж у, виконується нерівність

Тобто, можна оцінити ефективне значення показника якості проекту (R), приймаючи за показник ступеня ризику величину

Для сем і квадратичного відхилення у несприятливу сторону від медіани можна отримати аналогічну нерівність:

Отже, для заданого рівня надійності (або рівня значущості ) знайдеться k таке, що

А оскільки то

a ризик порушення останньої нерівності буде не більшим, ніж

Якщо прийняти за міру ризику величину SSV_М , отримаємо таку оцінку ефективного значення показника якості проекту:

Порівнявши оцінки зі значенням Rо, можна схвалюва­ти проект чи відхиляти його.

Запропонований нами підхід дає змогу в широкому спектрі фінансово-економічних проблем адекватно враховувати цілі суб'єктів господарювання, раціональну систему гіпотез, а також об'єктивно існуючу невизначеність і породжений нею ризик як об'єктивно-суб'єктивну економічну категорію.