3.1. Загальні підходи до кількісної оцінки ризику

У кожній ситуації, пов'язаній з ризиком, виникає питання: що означає виправданий (допустимий) ризик, де проходить межа, яка відокремлює допустимий ризик від загрозливого. Знати про існу­вання економічного ризику, аналізувати його необхідно, але не до­статньо. Важливо виявити його с ступінь, причому слід, зокрема, оці­нити ймовірність того, що певна (несприятлива) подія має шанси відбутись, а потім — яким чином це вплине на ситуацію (рішення).

За досить високого ступеня ризику в альтернативних стратегіях менеджери інколи приймають варіант рішення (стратегію) з дещо меншою економічною ефективністю (нормою прибутку, доходу) чи економічним ефектом, але з більшими шансами на своєчасну та ус­пішну (надійну) реалізацію прийнятого варіанта (стратегії).

Чим досконалішими є методи дослідження та кількісної оцін­ки ризику, тим меншим стає чинник невизначеності. Використо­вуються дві групи методів — апріорні та емпіричні. Перші ґрунтуються на теоретичних положеннях і формують вимоги щодо результатів певних рішень, другі — на вивченні минулих подій та опрацюванні інформації, зокрема статистичної.

Кількісна оцінка ступеня ризику провадиться на підставі об­числень, які здійснюються ще на попередній стадії. У прийнятті рішень треба враховувати можливість суперпозиції кількох об­ставин (сприятливих чи несприятливих) і визначити величину ймовірного прибутку або збитків, які виникають додатково. Як­що малоймовірно, що відбудуться несприятливі наслідки, то ри­зик малий. Малий він і в тому разі, коли ймовірність збитків ве­лика, а самі по собі обсяги збитків малі. Якщо вартість помилки велика, наприклад, у випадках з аваріями, людським життям, то їх ймовірність слід зробити дуже малою.

Важливими проблемами є розробка методик кількісної оцінки ризику в різних сферах економічної діяльності, розвиток відпові­дного механізму відстеження (моніторингу), контролювання економічного ризику та управління ним на засадах системного ана­лізу. Усе багатство людського інтелекту, накопичене, зокрема, в теорії ймовірностей і математичній статистиці, теорії корисності, теорії розпливчастих (нечітких) множин, якщо його використо­вувати конструктивно, може служити для побудови системи кі­лькісних оцінок ризику, із застосуванням тієї чи іншої системи гіпотез стосовно конкретної ситуації, пов'язаної з вибором з мно­жини альтернативних об'єктів (проектів) оптимального (раціональ­ного) рішення (проекту, стратегії) з відповідним (допустимим) сту­пенем ризику. Долаючи невизначеність і конфлікт, здійснюють перехід до ризику, переходять від невимірної невизначеності до ви­мірної. Це можна зробити, коли згідно з відокремленими цілями до­слідження приймається й відповідна система гіпотез.

Якщо перейти на формалізованішу мову, то «невизначеності» можна зіставити таку модель. Фіксується певний комплекс умов а, що накладається на систему S (реальну чи абстрактну), і спо­стерігається відповідний результат . Якщо за решти рівних умов можливими є різні результати , то ка­жуть про невизначеність щодо функціонування системи S в цих умовах. Не надто обмежуючи загальність подальших міркувань, можна припустити, що задано множину усіх можливих попарно різних результатів за фіксації комплексу умов . Додат­ково припустивши наявність деякої функції оцінювання v( ), що зіставляє кожному можливому результату його оцінку (V — множина різноманітних оцінок, впорядкованих за сту­пенем корисності, цінності, привабливості та інших), можна го­ворити про ризик щодо отримання результату .

У праці [283] наводиться приклад, де йдеться про фінансовий ін­вестиційний проект S. Початковий стан задається фіксацією ком­плексу умов , що описується вектором - обсяг коштів, витрачених на купівлю цінних паперів i-го виду; . Результуючий стан системи S можна описати, на­приклад, за допомогою вектора де — прирости за певний період реальної вартості і-го цінного паперу. Якщо цінністю результату є приріст реальної вартості всього інвестиційного портфеля, то можна говорити про невизначеність результату , встановленого «з точністю до множини », і про ри­зик малої фінансової ефективності інвестиційного проекту S.

Існує тлумачення терміну «ризик» як часткового випадку неви­значеності, пов'язаного з оцінкою низки можливих варіантів лише як несприятливих. Водночас необхідно наголосити на наявності в науковій літературі зовсім іншого трактування взаємозв'язку цих двох термінів [21, 283, 315, 327]. Часто словом «ризик» позначають ситуацію, коли для можливих варіантів визначена, зокрема, ймовір­ність їх появи, а словом «невизначеність» — ситуацію, коли визна­чити цю ймовірність неможливо. Таке розуміння термінів походить від відомої праці Ф. Найта «Ризик, невизначеніть і дохід» [315]. У цій науковій праці робиться протиставлення щодо можливості ста­тистичного чи теоретичного (апріорного, за термінологією Ф. Най­та) визначення ймовірностей варіантів.

Протягом багатьох років полярна пара «ризик— невизначе­ність» набула низки додаткових семантичних відтінків, втративши одночасно деякі первісні риси. Говорять про прийняття рішень в умовах ризику і прийняття рішень в умовах невизначеності.

У науковій праці [283] професор М. В. Хованов наголошує на неправомірності такого підходу. Натомість він пропонує розрізняти вимірювану та невимірну невизначеність за допомогою понять «не­визначеність першого роду» та «невизначеність другого роду». Не­визначеність першого роду має місце тоді, коли досліднику відома лише множина усіх можливих альтернативних варіантів поведін­ки досліджуваної системи, а невизначеність другого роду — тоді, коли є додатково відомий розподіл імовірності P, заданий на деякій сукупності підмножини , [283]. У цій праці на підставі теоретико-ймовірнісного підходу отримані досить вагомі результати.

Необхідно зазначити, що предикат «невизначеність» належить не до самого дослідника і не до окремо розглядуваної системи S, але до ситуації в цілому, описуючи реляцію між дослідником і досліджуваною системою [315]. Тобто терміном «невизначе­ність» фіксується наявність у дослідника дефіциту знань (інфор­мації) стосовно системи. Власне саме це не дозволяє однозначно визначити стан системи чи варіанти її поведінки.

На нашу думку, в ситуаціях оцінювання, управління, немину­чого вибору необхідно спиратися на наведені в першому розділі постулати, а також на визначення ризику, які становлять концеп­туальні засади для кількісного оцінювання ризику.

Отже, ризик зумовлюється необхідністю подолання невизна­ченості, конфлікту в ситуаціях ціле покладання, оцінювання, управління, неминучого вибору.

Конфлікт необхідно розуміти в двох аспектах: як внутрішній конфлікт суб'єкта ризику — множина цілей, множина критеріїв, неоднорідність самого суб'єкта ризику (структури) тощо; як зовні­шній конфлікт, тобто наявність контрагентів, конкурентів і необхід­ність для суб'єкта ризику враховувати альтернативні варіанти їх поведінки. Наголосимо також, що подолання невизначеності й конф­лікту зовсім не означає того, що невизначеність усувається (зникає). Зовсім не це мається на увазі. Адже ризик зумовлений існуванням невизначеності, тобто існування невизначеності й конфлікту, влас­не, і породжує ризик, яким обтяжений суб'єкт ризику, котрий зму­шений оцінювати, управляти, приймати рішення.

Подолання невизначеності розуміється нами в сенсі того, що суб'єкт ризику приймає низку обґрунтованих (раціональних) гі­потез, що дає йому змогу здійснити на пів впорядкування множи­ни можливих станів системи чи варіантів її поведінки. Зрозуміло, що невизначеність залишається, але суб'єкт сприймає та врахо­вує ризик, оцінюючи його, вводячи міру ризику. Зазначимо, що в ризикології не все так просто й ставити крапку щодо проблем по­лярної пари «ризик — невизначеність» ніхто в наш час не нава­житься. Але задача мінімізації ризику чи функціонування сис­теми у межах прийнятного ризику у фінансово-економічній сфе­рі — це задача боротьби з невизначеністю.

Історично першим способом урахування невизначеності, як зазначається в [193], було винайдення ймовірностей. Тут зазна­чається, що особи, котрі спеціалізувалися на азартних іграх, були заінтересовані в оцінці частот тих чи інших подій, реалізуючі се­рію з достатньої кількості випробувань. Разом з тим з самого по­чатку було зрозуміло, що досліджувана частота тих чи інших значень, яких набуває випадкова величина, не є характеристика­ми одиночної (разової) події (однієї гри), а повної їх множини, що пізніше дістала назву генеральної сукупності. Успішне засто­сування імовірнісних методів у статистиці наприкінці XIX сто­ліття (у дослідженні масових і статистично однорідних демогра­фічних процесів) зробило методи теорії ймовірностей досить поширеними в усіх сферах буття. Використання ймовірностей для врахування випадковості, невизначеності стосовно очікува­них подій набуло ексклюзивного характеру. Доречним є таке ви­користання, де йдеться про однорідні події масового характеру, зокрема, в теорії масового обслуговування, теорії надійності.

Однак, починаючи з 50-х років XX століття, в академічній на­уці з'явились праці, що ставили під сумнів тотальне застосування імовірнісної теорії до врахування невизначеності й породженого нею ризику. Автори цих праць слушно зазначали, що класична ймовірність аксіоматично визначена як характеристика генераль­ної сукупності статистично однорідних випадкових подій. У тих випадках, коли статистична однорідність не має місця, застосу­вання класичних імовірностей в аналізі не є адекватним.

Реагуванням на ці аргументовані зауваження стала низка фунда­ментальних наукових праць, зокрема Севіджа, Пойя, Кайберга, Фіш-берна, де Фінетті та ін., де обґрунтовувалось впровадження некла-сичних імовірностей. Тобто таких імовірностей, що не мають часто­тного сенсу, а виражають пізнавальну активність дослідника (суб'єкта ризику) щодо випадкових процесів, який вимушений при­ймати рішення (оцінювати) в умовах дефіциту необхідної інформа­ції, котра в більшості випадків відсутня на момент прийняття рі­шення. Так з'явилися суб'єктивні (аксіологічні) ймовірності. Разом з тим більшість наукових результатів з класичної теорії ймовірнос­тей перебралася в теорію аксіологічних ймовірностей і, зокрема, у логіко-ймовірнісні схеми дедуктивного виведення інтегрованих ймовірностей складних подій, що базуються на побудові повної множини вихідних гіпотез щодо реалізації простих подій, котрі є складовими досліджуваної складної події. Ці схеми дістали назву імплікативних. Докладно про розвиток теорії ймовірностей протя­гом XX століття досить яскраво й переконливо описано в [161].

Водночас поява некласичних ймовірностей стала не єдиним реа­гуванням на виявлену проблему. Необхідно наголосити на підви­щенні зацікавленості до мінімаксних підходів, принципу гарантова­ного результату, а також на зародженні теорії нечітких множин. За мінімаксного підходу суб'єктові ризику, особі, що приймає рішення (ОПР), пропонується відреагувати на ситуацію так, аби домогтися найкращих (у певному сенсі) результатів за найгірших умов. Вважа­ється, що така поведінка є оптимальною в умовах невизначеності й породженого нею ризику. Опонуючи мінімаксним підходам, учені (дослідники) зазначають, що очікування найгірших сценаріїв може виявитися вкрай обережним (коли особа є гранично несхильною до ризику), і це налаштовуватиме систему прийняття рішень на найнесприятливіші результати, що призведе, в свою чергу, до паралічу економічних інновацій, виникненню ризику невикористаних мож­ливостей («закопаних талантів»).

Компромісом щодо мінімаксних підходів є метод Гурвіця [44, 255], коли два екстремальні сценарії (найгірший і найкращий) ура­ховуються спільно, а за ваговий коефіцієнт у згортці сценаріїв ви­ступає параметр , значення котрого задається ОПР. Чим більшого значення набуває , тим оптимістичніше налаштована ОПР. Але за такого підходу губиться (не враховується) наявна ін­формація, що її дають решта сценаріїв (окрім мінімального та мак­симального ефектів). Модифікацією інтегрально-ймовірнісного ме­тоду Гурвіця є метод, який враховує додаткову інформацію щодо співвідношення ймовірностей наявної множини сценаріїв з урахуванням того, що точні значення сценарних імовірностей невідомі [193].

Стосовно нечітких множин, то первісною ідеєю цієї теорії бу­ло прагнення побудувати функціональну відповідність між нечіт­ким лінгвістичним описом (типу «високий», «теплий» тощо) і відповідними спеціальними числами, що виражають ступінь аде­кватності значень вимірюваних параметрів (довжина, температу­ра, вага тощо) згаданому нечіткому опису [137]. У цій праці Лофті Заде були впроваджені так звані лінгвістичні ймовірності — ймовірності, що задаються не кількісно, а за допомогою нечітко-змістовного оцінювання. Згодом сфера застосування теорії нечіт­ких множин суттєво розширилась. Сам Л. Заде визначив нечіткі множини як інструмент побудови теорії можливостей [354]. З тих пір наукові категорії випадковості й можливості, ймовірності й ступінь належності отримують теоретичне розмежування.

Черговим досягненням теорії нечітких (розпливчастих) мно­жин є впровадження таких понять, як нечіткі числа нечітких підмножин спеціалізованого виду, що відповідають висловлюван­ням (судженням) типу "значення змінної приблизно дорівнює а". З їх запровадженням стало можливим прогнозувати майбутні значення параметрів, котрі очікуються як значення в деякому ді­апазоні (інтервалі). Вибудовується також набір операцій над не­чіткими числами, котрі приводяться до алгебраїчних операцій із звичайними числами за задання певного інтервалу належності.

Прикладні результати теорії нечітких множин, як про це йдеться, зокрема, в [193], не примусили себе довго очікувати. Закордонний ринок так званих нечітких контролерів (різновид яких встановлено навіть на пральних машинах марки LG) оцінюють ємністю в мілья­рди доларів. Набуває поширення як модель людських розумових процесів нечітка логіка, вбудована в системи штучного інтелекту й автоматизовані системи підтримки прийняття рішень тощо.

Починаючи з кінця 70-х років XX століття методи теорії нечіт­ких множин починають застосовуватися в економіці. Серед низки публікацій вийшла друком і монографія [160], у котрій подано ши­рокий спектр можливих застосувань цієї теорії, починаючи від оці­нки ефективності інвестицій до кадрових рішень і заміни устатку­вання. Побудовані й відповідні економіко-математичні моделі.

У [193] зазначається, що суттєвою перевагою теорії ймовірно­стей і математичної статистики є історичний (протягом кількох століть) досвід застосування й використання ймовірностей та ло­гічних схем на їх підґрунті. Але коли невизначеність щодо май­бутнього стану об'єкта дослідження губить риси статистичної невизначеності, класична ймовірність як характеристика масових процесів відходить у небуття. Погіршення інформованої спонукає до використання суб'єктивних імовірностей, але тут же виникає й проблема достовірності ймовірнісних оцінок ОПР: приписуючи ймовірностям точкові значення в ході деякої віртуальної простої ло­тереї, керуються міркуваннями власних економічних переваг, котрі можуть бути деформовані сподіваннями й пристрастями.

У виборі оцінок суб'єктивних імовірностей нерідко посилаються на відомий принцип Гібса—Джейнса: серед усіх імовірнісних роз­поділів, узгоджених з вихідною (первісною) інформацією стосовно невизначеності відповідного показника, рекомендується обрати той, котрому відповідає максимальна ентропія. Багато дослідників, зок­рема й автор [193], і автори цієї монографії [52, 83], залюбки вико­ристовували даний метод. Однак цей принцип необхідно застосову­вати обережно, бо він не забезпечує автоматично монотонності критерія сподіваного ефекту [255]. Отже, принцип максимуму ент­ропії необхідно доповнювати граничними умовами застосовуванос-ті цього критерію щодо вибору ймовірнісних розподілів.

У разі ж застосування нечітких чисел від ОПР вимагається не формулювати точкові ймовірнісні оцінки, а задавати розрахунко­вий коридор значень прогнозованих параметрів. У такому разі сподіваний ефект оцінюється експертом так само, як і нечітке чи­сло зі своїм розрахунковим розкидом (ступенем нечіткості). Як зазначається в низці праць, за такого підходу виникає алгоритмі­чна й програмна перевага методу, що ґрунтується на нечіткості, оскільки дослідник оперує не опосередкованими оцінками (до яких можна віднести ймовірності), а, зокрема, прямими проект­ними даними щодо розкиду (варіації) параметрів.

Стосовно оцінки ступеня ризику при прийнятті рішень в умо­вах невизначеності, то, як зазначається в низці наукових праць, імовірнісні й нечітко-множинні методи дають дослідникові дода­ткові можливості аналізу залежно від цілей і прийнятих гіпотез. Ступінь стійкості рішень, чутливих щодо коливання вихідних даних, верифікується в процесі їх аналізу, і ця стійкість може бу­ти оцінена аналітично, що має принципове значення.

Зазначимо, що на сьогодні можна виокремити низку матема­тичних теорій, що їх доречно застосовувати для формалізації не-визначеної інформації й вимірювання ризику [31]:

1. Багатозначна логіка.

2. Теорія ймовірностей.

3. Теорія похибок (інтервальні моделі).

4. Теорія інтервальних середніх.

5. Теорія суб'єктивних імовірностей.

6. Теорія нечітких множин.

7. Теорія нечітких мір й інтегралів.

Проведений аналіз (порівняння) цих теорій показав, що однією з найефективніших математичних теорій, з погляду її викори­стання в проблемах невизначеності і породженого нею ризику, є теорія нечітких мір [31]. Але, незважаючи на бурхливий розвиток цієї теорії протягом останніх десятиліть, математичні підходи, що використовують нечіткі міри, ще недостатньо розвинуті і за­лишається низка питань щодо їх практичного застосування в економіці та підприємництві. З часу перших публікацій з основ теорії нечітких мір [347] пройшло понад ЗО років. Найбільший розвиток і практичне застосування отримали дослідження з пи­тань міри можливості й необхідності [120, 197]. Вказані галузі знань, особливо математичні моделі нечітких процесів, бурхливо розвиваються.

Кількісна оцінка ризику базується на результатах його кількі­сного та якісного аналізу. Ще раз наголосимо, що якісний аналіз ризику є найскладнішим і вимагає ґрунтовних знань, досвіду та інтуїції в сфері конкретної діяльності [52]. У процесі кількісного оцінювання ризику якісний і кількісний аналіз не механічно до­повнюють один одного, а системно взаємодіють. Кількісний ана­ліз може мати в основі лише якісно встановлені цілі, гіпотези, критерії, чинники, умови, альтернативи, відображати ставлення до ризику його суб'єкта. В свою чергу, якісний аналіз можна вдо­сконалити, використовуючи результати кількісного аналізу. Зок­рема, якщо внаслідок кількісного аналізу чинників ризику вдало­ся встановити недостатню достовірність їх впливу, то це є підставою для перегляду висновків якісного аналізу й проведення ґрунтовніших досліджень з метою встановлення реально суттє­вих чинників ризику (ключових параметрів).

Зазначимо, що в теорії досить поширеною і розумною є гіпо­теза, що варіація відносно середнього (математичного сподіван­ня) ефекту (наприклад, прибутку) може бути одним з безлічі по­казників кількісної оцінки ступеня економічного ризику. Ма­тематичним виразом варіації відносно середнього як однієї з кі­лькісних оцінок ступеня економічного ризику традиційно при­ймається дисперсія та середньоквадратичне відхилення [83]. На нашу думку, цілком чітко можна зазначити, що обчислення сере­дньоквадратичного відхилення норми прибутку деякого активу як оцінки ступеня ризику ще не є завершеною оцінкою міри ри­зику, бо суб'єктові ризику необхідно ще співвіднести середньо-квадратичне відхилення до необхідної норми прибутку щодо да­ного класу активів і до рівня ефективності й ступеня її варіа-бельності в альтернативних варіантах. Таке співвіднесення може завершити кількісну оцінку ступеня ризику, але не оцінку ризику загалом (щодо даної операції), оскільки для реалізації останнього необхідно враховувати ставлення ОПР до ризику. Одні й ті самі кількісні оцінки сприймаються різними ОПР як такі, що характеризують різний ступінь і грань ризику. Отже, необхідно врахува­ти ставлення до ризику його суб'єктів. Тому в концептуальному сенсі кількісна оцінка ґрунтується на:

1. якісному аналізі ризику;

2. кількісному аналізі ризику;

3. ставленні до ризику його суб'єкта.

Ризик є характерним феноменом ринкової економіки, потре­бує ретельного аналізу впливу на об'єкти (процеси) оцінювання та управління множини внутрішніх і зовнішніх чинників, над системи, а також урахування ставлення до ризику суб'єктів господа­рювання (суб'єктів ризику). Наведене у попередньому матеріалі означення ризику та система постулатів також вказують на необ­хідність урахування діалектичної об'єктивно-суб'єктивної струк­тури ризику, здійснюючи його якісний і кількісний аналіз, визна­чаючи кількісну оцінку міри ризику, моделюючи його та управляючи ним.

Необхідно, щоб міра ризику відображала міру (ступінь) відхи­лення від цілей, бажаного (очікуваного) результату, міру невдачі (збитків) з урахуванням впливу керованих (контрольованих) і некерованих (неконтрольованих) чинників, прямих і зворотних зв'язків, враховувала різні грані цього феномену економічного буття. Отже, можна дійти висновку, що кількісна міра ризику є вектором, компоненти якого відображають різні грані ризику і формуються залежно від цілей дослідження, прийнятої системи гіпотез, наявної Інформації, ставлення суб'єкта ризику до неви­значеності, конфліктності.

Вимірювання ризику повинно ґрунтуватися на загально методологічних положеннях теорії вимірювань, що складає науковий фундамент будь-яких вимірювань. Стосовно оцінки економічно­го ризику вимірюваними властивостями економічних систем по­винні бути такі характеристики структури, стану чи поведінки цих систем та їх зовнішнього середовища, котрі дозволяють за умов невизначеності та конфлікту віднайти і диференціювати за потенційними наслідками можливі майбутні стани чи траєкторії (їх множину) поведінки певних економічних об'єктів, можливі відхилення від цілей, можливі збитки. Виявлення таких власти­востей є предметом якісного та кількісного аналізу ризику і поля­гає у виявленні ключових параметрів (чинників ризику) та іден­тифікації форм, видів і типів ризику. Методологічні засади і мето­дичні підходи такого аналізу викладені у попередніх розділах да­ної роботи.

Як приклад застосування теорії вимірювань до вирішення пи­тань ризикології з урахуванням специфіки цієї науки [288] запро­поновано узагальнений алгоритм розробки методики вимірюван­ня певних видів і показників економічного ризику. Наведемо цей алгоритм (рис. 3.1).

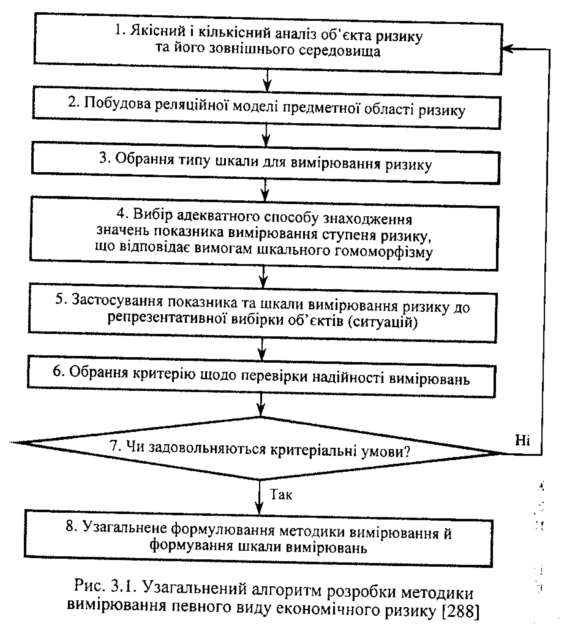
Реляційна модель являє собою відображення предметної обла­сті у вигляді

множини, що задає сукупність відношень. У теорії вимірювань таку множину називають системою з відношеннями. У найпростіших випадках це можуть бути відношення еквівален­тності й порядку. Водночас система відношень може визначатися і за допомогою різноманітних операцій (наприклад, бісекції, су­ми, добутку тощо), що створюють так звану алгебру. За посеред­ництвом алгебри логіки та відповідних шкал конструюються ін­тегровані показники міри ризику на підґрунті окремих компонент вектора міри ризику

Зазначимо, що необхідно прагнути використовувати наявні можливості вимірювання у відносних чи хоча б інтервальних шкалах. Як вимірювач може виступати відображення, що є гомо­морфізмом з емпіричної реляційної системи у шкальну числову систему з реляціями [288]. Відповідно до теорії вимірювань го­моморфізм визначається не однозначно, тобто існує множина шкал, що гомоморфно відображає певну емпіричну систему з ре­ляціями [225]. У зв'язку з цим суттєву роль відіграє четвертий блок наведеного узагальненого алгоритму (див. рис. 3.1), функ­цією котрого є визначення та обґрунтування вибору того чи ін­шого показника як вимірювача, що є адекватним предметній сфері вимірюваного ризику, її емпіричній системі з реляціями, цілям дослідження та прийнятій системі гіпотез. Аналіз наукових публікацій свідчить, що у вимірюванні економічного ризику отримали практичне застосування майже всі типи шкал, окрім номінальних.

Виходячи зі змістовного визначення економічного ризику, йо­го ієрархічності, множинності чинників ризику тощо, можна стверджувати про принципову неможливість вичерпного вимі­рювання ризику за окремою його емпіричною властивістю. За­значимо, що окремі показники ступеня ризику обчислюють у відносних або абсолютних величинах. Велике значення для оцін­ки ступеня ризику має вибір економічних показників, за варіацією, мінливістю, швидкістю змін яких судять про міру ризику. Необ­хідно, щоб ці показники відображали економічну сутність ре­зультатів оцінювання, управління, рішення та були адекватними щодо обраних цілей і прийнятої системи гіпотез.

Зазначимо, що кількість показників ступеня ризику в економі­ці та підприємництві весь час зростає й зростатиме надалі через багатогранність ризику. Тому є сенс продовжувати наукові до­слідження в даній сфері.