Задачи тестов

1.Смесь идеальных газов состоит из двух компонентов. Их парциальные давления равны р₁ = 1000 Па,  р₂ = 100 Па. Полное давление составляет ___ кПа.

2.Объемные доли водорода и аргона r_H2 = 10 %,  r_O2 = 2 %. Массовая доля водорода равна _____%.

Решение: = /( + . ??!!

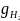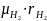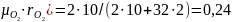Задача. Объемный состав сухих продуктов сгорания топлива (не содержащих водяных паров) следующий: 12,3% СО₂, 7,2% О₂, 80,5% N₂.

Найти кажущуюся молекулярную массу смеси и газовую постоянную, а также плотность и удельный объем продуктов сгорания при давлении 100 кПа и температуре 800 ˚С.

Дано: r_CO2 = 0,123; μ_CO2 = 44 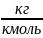, r_O2 = 0,072; μ_О2 = 32 , r_N2 = 0,805; μ_N2 = 28 к P = 100 кПа = 10⁵ Па, t = 800 ˚С. Найти: μ_см, R_см, ρ_cм, ν_см

Решение: Кажущуюся молекулярную массу определяем из уравнения (1.19)

μ_см = Σ r μ = r_СО2·μ_СО2 + r_O2·μ_O2 + r_N2·μ_N2 = 0,123⋅44 + 0,072⋅32 + 0,805⋅28 = 30,3 .

Газовую постоянную – из уравнения (1.17): R_cм = = = 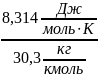274 .

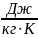Удельный объем находим из уравнения состояния идеального газа (1.8)

ν_см =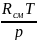 = = 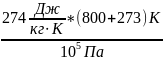2,94

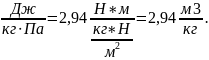
Находим плотность ρ_см = 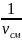= = 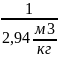0,34 .

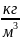1.5. Теплоемкость газа

Теплоёмкостью тела называется количество теплоты, необходимое для изменения его температуры на 1 К.

Истинная теплоемкость рабочего тела определяется отношением количества подведенной (отведенной) к рабочему телу теплоты в данном термодинамическом процессе к вызванному этим изменениям температуры тела:

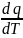
C = 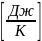(1.25)

Для практических расчетов удобно пользоваться средними теплоемкостями, значения которых даются в справочных таблицах или подсчитываются по эмпирическим формулам.

Средняя теплоемкость относится к интервалу температур, а истинная к конкретной температуре.

Г еометрически средняя теплоемкость представляет собой высоту прямоугольника 1’342', площадь которого равна площади 1’122' под кривой с(Т) (рис.1). Каждая из этих площадей численно равна удельной теплоте, подведенной к рабочему телу в интервале температур Т₁ –Т₂:

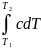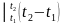q = = c_cp . (1.26)

При пользовании такими теплоемкостями, удельную теплоту подсчитывают по выражению

c =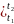

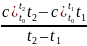
Теплоемкость зависит от внешних условий или характера процесса, при котором происходит подвод или отвод теплоты.

Рис.1. Средняя теплоемкость .

в интервале температур Т₁-Т_{2 /}

Различают следующие удельные теплоемкости:

массовую: c = ;

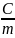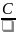
молярную: μc = 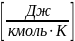, где 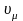– количества вещества [кмоль];

объемную:, c = .

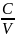
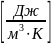Связь между этими теплоемкостями:

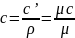
где 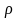– плотность вещества, 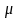– молярная (молекулярная) масса, [кг/кмоль].

Теплоемкость газов в большой степени зависит от тех условий, при которых происходит процесс их нагревания или охлаждения. Различают теплоемкости при постоянном давлении (изобарную) и при постоянном объеме (изохорную):

с_р, с_v – массовые изобарные и изохорные теплоемкости;

μс_р , μс_v – молярные изобарные и изохорные теплоемкости;

с_р´ , с_v´ –объемные изобарные и изохорные теплоемкости.

Связь между изобарной и изохорной теплоемкостями дается уравнением Майера

с_р - с_v = R_µ (1.27)

μс_р -μс_v = R₀ (1.28)

В процессе v=const теплота, сообщаемая газу, идет лишь на изменение его внутренней энергии, тогда как в процессе p=const теплота расходуется и на увеличение внутренней энергии и на совершение работы против внешних сил.

Поэтому с_р больше с_v на величину этой работы. Следовательно, газовая постоянная R_µ численно равна работе расширения одного килограмма газа при на-гревании его при постоянном давлении на один градус.

Для реальных газов с_р - с_v > R_µ, поскольку при расширении реальных газов (при p=const) совершается работа не только против внешних сил, но и против сил притяжения, действующих между молекулами, что вызывает дополнительный расход теплоты.

Удельные массовые изохорная с_v и изобарная с_p теплоемкости определяются по соотношениям молекулярно-кинетической теории:

с_v=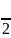 R_µ, с_p=с_v+ R_µ=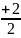 R_µ, (1.29)

где i - число степеней свободы молекулы идеального газа (для одноатомного газа i=3, двухатомного - i=5, трехатомного и более - i=6).

Для молярных теплоемкостей это даёт:

для одноатомных rазов: µс_v = 12,4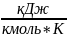8 ; µс_р = 20,8 ;

для двухатомных rазов: µс_v = 20,8 ; µс_р = 29,12 .

Из (1.29) следует, что показатель адиабаты k = 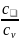= 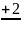. Тогда для одноатомных rазов k =1,67, для двухатомных k =1,40, для трехатомных и более k =1,33.