11. Универсальный метод информационных технологий – статистическое моделирование нелинейных систем со случайными характеристиками в условиях помех (метод Монте-Карло).

Ме́тод Мо́нте-Ка́рло (методы Монте-Карло, ММК) — общее название группы численных методов, основанных на получении большого числа реализаций стохастического (случайного) процесса, который формируется таким образом, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи. Используется для решения задач в различных областях физики, химии, математики, экономики, оптимизации, теории управления и др.

Во всех случаях, когда имитация функционирования системы осуществляется в условиях случайных воздействий и помех, эксперимент приобретает статистический характер, поскольку обработка результатов имитации должна проводиться с использованием статистических методов.

Статистическое моделирование представляет собой метод получения с помощью ЭВМ статистических данных о процессах в моделируемой системе. Можно сказать, что имитационное моделирование систем в общем случае есть ни что иное, как статистическое моделирование.

Статистическое моделирование охватывает широкий круг вопросов и использует различные методы. Задача осложняется еще тем, что в общем случае исследователь априори не располагает конкретными данными о законах распределения и других статистических характеристиках воздействий и разброса параметров компонентов исследуемой системы (из-за нестабильности технологических процессов, изменения исходных материалов и т.п.). Требуется накопление и обобщение этих сведений, корректировка накопленных статистических данных.

Статистическое моделирование может быть использовано при решении детерминированных задач. Статистический анализ в этом случае применяют после получения, например, оптимального решения детерминированной задачи в номинальном режиме. Окончательному суждению о качестве полученного решения должно предшествовать выполнение статистического анализа, который даст ответ на вопрос об отклонениях выходных параметров от номинальных при замене детерминированной задачи на эквивалентную статистическую.

Одним из широко применяемых методов статистического анализа является метод Монте-Карло. Исходными данными для анализа являются внутренние Х={х₁, х₂,…, х_n} и внешние параметры F= {f₁, f₂, …, f_k} (воздействие среды — сигналы, нагрузка, температура, помехи и т.п.), а результатом решения — определение выходных параметров исследуемого объекта Y= G (X, F).

При производстве изделий и в процессе их эксплуатации имеются неизбежные отклонения от номинальных (требуемых) значений X и F, что приводит к отличию У от Уном. Поэтому окончательное суждение о качестве изделия можно сделать после выполнения статистического анализа, позволяющего оценить рассеяния выходных параметров относительно номинальных (требуемых) значений.

Метод Монте-Карло реализует статистический анализ на основе статистических испытаний. В этом случае исходной информацией являются числовые характеристики закона распределения внутренних параметров X и допустимые диапазоны изменения внешних параметров F, а результатом — числовые характеристики закона распределения У.

Алгоритм метода включает выполнение N-испытаний (опытов). В каждом испытании задаются случайные значения х_i, и f_j в соответствии с их законом распределения и определяются случайные значения параметров у_k.

Схема вычислений методом Монте-Карло представлена на рисунке ниже. В методе многократно (N раз) повторяется детерминированный, одновариантный расчет; N должно быть достаточно большим, чтобы выборка была представительной.

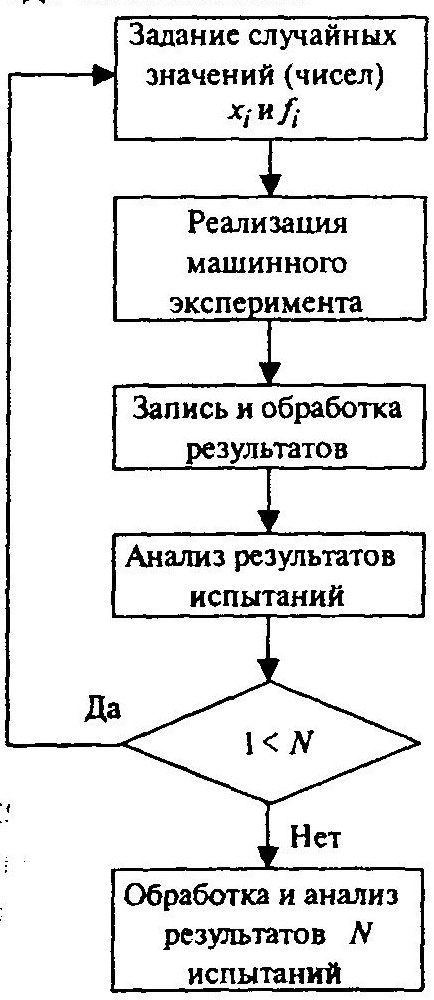Схема вычислений методом Монте-Карло

Метод статистических испытаний успешно применяется, например, при статистическом анализе микросхем, интегральных схем. Эти схемы имеют большую размерность, нелинейные и корреляционные связи между параметрами, что существенно осложняет прямые аналитические расчеты. Метод Монте-Карло реализует вариантный расчет и, по существу, представляет собой численный метод решения аналитической задачи.

Существует ряд программных комплексов для реализации статистических экспериментов методом Монте-Карло.

12. Моделирование АСОИУ (виды математических моделей и имитационное моделирование, детерминированные и стохастические модели, нечеткие модели; основные этапы создания математических моделей; аналитический и экспериментальный способы создания математических моделей; классификация биотехнологических систем как объектов математического моделирования, классификация математических моделей биотехнологических систем; классификация экономических систем как объектов моделирования, классификация математических моделей экономических систем).

Математи́ческая моде́ль — это математическое представление реальности^[1].

Математическое моделирование — это процесс построения и изучения математических моделей.

Все естественные и общественные науки, использующие математический аппарат, по сути занимаются математическим моделированием: заменяют объект его математической моделью и затем изучают последнюю. Связь математической модели с реальностьюосуществляется с помощью цепочки гипотез, идеализаций и упрощений. С помощью математических методов описывается, как правило, идеальный объект, построенный на этапе содержательного моделирования.

Формальная классификация моделей основывается на классификации используемых математических средств. Часто строится в форме дихотомий. Например, один из популярных наборов дихотомий ^[9]:

• Линейные или нелинейные модели^[10];

• Сосредоточенные или распределённые системы^[11];

• Детерминированные или стохастические^[12];

• Статические или динамические^[12];

• Дискретные или непрерывные ^[12].

и так далее. Каждая построенная модель является линейной или нелинейной, детерминированной или стохастической, … Естественно, что возможны и смешанные типы: в одном отношении сосредоточенные (по части параметров), в другом — распределённые модели и т. д.

Наряду с формальной классификацией, модели различаются по способу представления объекта:

• Структурные или функциональные модели

Структурные модели представляют объект как систему со своим устройством и механизмом функционирования. Функциональные модели не используют таких представлений и отражают только внешне воспринимаемое поведение (функционирование) объекта. В их предельном выражении они называются также моделями «чёрного ящика».^[13] Возможны также комбинированные типы моделей, которые иногда называют моделями «серого ящика».

Для поддержки математического моделирования разработаны системы компьютерной математики, например, Maple, Mathematica, Mathcad, MATLAB, VisSim и др.^[24] Они позволяют создавать формальные и блочные модели как простых, так и сложных процессов и устройств и легко менять параметры моделей в ходе моделирования. Блочные модели представлены блоками (чаще всего графическими), набор и соединение которых задаются диаграммой модели.

Имитационное моделирование (ситуационное моделирование) — метод, позволяющий строить модели, описывающие процессы так, как они проходили бы в действительности. Такую модель можно «проиграть» во времени как для одного испытания, так и заданного их множества. При этом результаты будут определяться случайным характером процессов. По этим данным можно получить достаточно устойчивую статистику.

Имитационное моделирование — это метод исследования, при котором изучаемая система заменяется моделью, с достаточной точностью описывающей реальную систему, с которой проводятся эксперименты с целью получения информации об этой системе. Экспериментирование с моделью называют имитацией (имитация — это постижение сути явления, не прибегая к экспериментам на реальном объекте).

Имитационное моделирование — это частный случай математического моделирования. Существует класс объектов, для которых по различным причинам не разработаны аналитические модели, либо не разработаны методы решения полученной модели. В этом случае аналитическая модель заменяется имитатором или имитационной моделью.

Имитационным моделированием иногда называют получение частных численных решений сформулированной задачи на основе аналитических решений или с помощью численных методов^[1].

Имитационная модель — логико-математическое описание объекта, которое может быть использовано для экспериментирования на компьютере в целях проектирования, анализа и оценки функционирования объекта.

К имитационному моделированию прибегают, когда :

• дорого или невозможно экспериментировать на реальном объекте;

• невозможно построить аналитическую модель: в системе есть время, причинные связи, последствие, нелинейности, стохастические (случайные) переменные;

• необходимо сымитировать поведение системы во времени.

Цель имитационного моделирования состоит в воспроизведении поведения исследуемой системы на основе результатов анализа наиболее существенных взаимосвязей между её элементами или другими словами — разработке симулятора (англ. simulation modeling) исследуемой предметной области для проведения различных экспериментов.

Имитационное моделирование позволяет имитировать поведение системы во времени. Причём плюсом является то, что временем в модели можно управлять: замедлять в случае с быстропротекающими процессами и ускорять для моделирования систем с медленной изменчивостью. Можно имитировать поведение тех объектов, реальные эксперименты с которыми дороги, невозможны или опасны. С наступлением эпохи персональных компьютеров производство сложных и уникальных изделий, как правило, сопровождается компьютерным трёхмерным имитационным моделированием. Эта точная и относительно быстрая технология позволяет накопить все необходимые знания, оборудование и полуфабрикаты для будущего изделия до начала производства^{[источник не указан 229 дней]}. Компьютерное 3D моделирование теперь не редкость даже для небольших компаний^{[источник не указан 229 дней]}.

Имитация, как метод решения нетривиальных задач, получила начальное развитие в связи с созданием ЭВМ в 1950-х — 1960-х годах.

Можно выделить две разновидности имитации:

• Метод Монте-Карло (метод статистических испытаний);

• Метод имитационного моделирования (статистическое моделирование).

Виды имитационного моделирования

• Агентное моделирование — относительно новое (1990-е-2000-е гг.) направление в имитационном моделировании, которое используется для исследования децентрализованных систем, динамика функционирования которых определяется не глобальными правилами и законами (как в других парадигмах моделирования), а наоборот, когда эти глобальные правила и законы являются результатом индивидуальной активности членов группы. Цель агентных моделей — получить представление об этих глобальных правилах, общем поведении системы, исходя из предположений об индивидуальном, частном поведении её отдельных активных объектов и взаимодействии этих объектов в системе. Агент — некая сущность, обладающая активностью, автономным поведением, может принимать решения в соответствии с некоторым набором правил, взаимодействовать с окружением, а также самостоятельно изменяться.

• Дискретно-событийное моделирование — подход к моделированию, предлагающий абстрагироваться от непрерывной природы событий и рассматривать только основные события моделируемой системы, такие как: «ожидание», «обработка заказа», «движение с грузом», «разгрузка» и другие. Дискретно-событийное моделирование наиболее развито и имеет огромную сферу приложений — от логистики и систем массового обслуживания до транспортных и производственных систем. Этот вид моделирования наиболее подходит для моделирования производственных процессов. Основан Джеффри Гордоном в 1960-х годах.

• Системная динамика — парадигма моделирования, где для исследуемой системы строятся графические диаграммы причинных связей и глобальных влияний одних параметров на другие во времени, а затем созданная на основе этих диаграмм модель имитируется на компьютере. По сути, такой вид моделирования более всех других парадигм помогает понять суть происходящего выявления причинно-следственных связей между объектами и явлениями. С помощью системной динамики строят модели бизнес-процессов, развития города, модели производства, динамики популяции, экологии и развития эпидемии. Метод основан Джеем Форрестером в 1950 годах.

В зависимости от способа отражения причинно-следственных связей и требований практики управления проектом все математические модели можно разделить на детерминированные и стохастические.

Модели, в которых значения переменных предполагаются заведомо заданными при жестких связях и условно достоверными, принято называть детерминированными. Среди них по степени математической абстракции или сглаженности значений переменных можно выделить два типа экономико-математических структур: сложные и упрощенные. Сложные экономико-математические модели дают более точные результаты, но требуют большого объема исходной информации и специального программного обеспечения. Ограниченность времени, отводимого на подготовку и принятие решений вообще и в системах управления проектом особенно, препятствует широкому применению этих моделей. Поэтому в практике управления проектами чаще всего используются достаточно простые модели.

Особое место занимают сетевые модели (графики), являющиеся графоаналитическими, что позволяет в наглядной форме описывать весь производственный процесс: от зарождения идеи проекта до его реализации.

Как правило, реализация детерминированного подхода к моделированию анализа и принятия решений предполагает, с одной стороны, получение однозначного решения, а с другой — уточнение этих решений путем ввода элемента случайности в терминах теории вероятностей. Последнее дает возможность оценить последствия непредвиденных сбоев, например срыв сроков проектирования или строительства зданий и сооружений, намеченных утвержденным ранее планом. При этом математическое моделирование детерминированных процессов становится частным случаем применения стохастических, вероятностных подходов.

Если в модели среди величин имеются случайные, т.е. определяемые лишь некоторыми вероятностными характеристиками, то модель называется стохастической (вероятностной, случайной). В этом случае и все результаты, полученные при рассмотрении модели, имеют стохастический характер и должны быть соответственно интерпретированы. Здесь подчеркнем, что с точки зрения практики граница между детерминированными и стохастическими моделями выглядит расплывчатой. Так, в технике про любой размер или массу можно сказать, что это не точное значение, а усредненная величина типа математического ожидания, в связи с чем и результаты вычислений будут представлять собой лишь математические ожидания исследуемых величин. Однако такой взгляд представляется крайним. Удобный практический прием состоит в том, что при малых отклонениях от фиксированных значений модель считается детерминированной, а отклонение результата исследуется методами оценок или анализа ее чувствительности. При значительных же отклонениях применяется методика стохастического исследования.

При моделировании сложных систем и процессов исследователи часто сталкиваются с невозможностью построения аналитической модели изучаемого объекта, либо слишком большой сложностью такой модели, либо отсутствием достаточного опыта для построения экспертных систем, либо недостаточностью экспериментальных данных для статистического моделирования. Решением проблемы может быть переход от аналитических или статистических моделей к нечетким. Собственно моделирование осуществляется посредством системы не­четкого вывода, которая выполняет следующие действия: 1) преобразует числовую информации в лингвистические переменные (процесс фаззификации); 2) обрабатывает лингвистическую информацию, выполняя логические операции нечеткой конъюнкции, импликации и агрегации правил; 3) формирует числен­ные результаты (процесс дефаззификации) [1].

Нечеткая модель может быть построена либо на основе знаний эксперта, либо на основе наблюдаемых данных, либо на совместном использовании зна­ний и данных. Идентификация рассматривается в настоящей работе как этап по­строения модели, связанный с установлением закономерностей между входны­ми и выходными переменными объекта.

Нечеткая модель определена как система с n входными переменными X = {X₁, X₂,..., X_n}, определенными на входной области рассуждений DX = DX₁ x DX₂ x... x DX_n, и одной выходной переменной Y, определенный на выходной области рассуждений DY. Четкое значения, которое принимает вход­ная переменная Xi, обозначается как xi, и как y для выходной переменной Y.

Нечеткая область определения i-ой входной переменной X_i, обозначена как FX_i = {LX_ii1,..., LX_i,pi}, где pi - количество лингвистических термов (нечетких значений), на которых определена входная переменная, LXi,k задает функцию принадлежности и имя k-го лингвистического терма. Аналогично, FY = {LY₁,..., LY_q} - нечеткая область определения выходной переменной, q - число нечетких значений, LYj - функция принадлежности и имя выходного лингвистического терма.

Нечеткое j-ое правило в модели типа синглтон имеет вид

База правил в модели типа Мамдани представляет собой множество нечет­ких правил вида

rj - действительное число, которым оценивается выход y.

Нечеткая система осуществляет отображение F :

R^п ^ℜ

R . Важную роль в этом отображении играют функции принадлежности mL_Xij(x_i), указывающие сте­пень принадлежности четкой переменной X_i нечеткому понятию LXj. Каждая функция принадлежности задается своим набором параметров, например, тре­угольная - тройкой параметров, трапециевидная - четверкой, гауссова и пара­болическая - двойкой.

Обучение модели ведется на основе таблиц наблюдений или тестовых функций f(x). Необходимо так построить базу правил, чтобы ошибка вывода, определяемая как

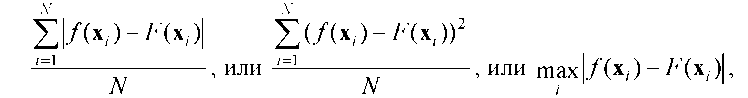
была минимальной.

В общем, построение нечеткой модели состоит из четырех основных эта­пов: 1) экспертное оценивание - задание типа нечеткой модели и сопутствую­щих этому типу параметров; 2) идентификация структуры - выбор переменных (X, DX, Y, DY, pi, q) и нечетких правил (R_j); 3) оценка параметров - поиск опти­мальных значений всех параметров, задействованных в нечеткой модели, т. е. нахождение значений консеквентна и параметров функций принадлежности в ан­тецеденте каждого правила (FX_i, FY) на основе заданных критериев качества и метода оптимизации выбранного критерия); 4) проверка правильности модели.

Сущность построения математической модели состоит в том, что реальная система упрощается, схематизируется и описывается с помощью того или иного математического аппарата. Выделяют следующие основные этапы построения моделей. 1. Содержательное описание моделируемого объекта. Словесно описывается объект моделирования, цели его функционирования, среда, в которой он функционирует, выявляются отдельные элементы, возможные состояния, характеристики объекта и его элементов, определяются взаимосвязи между элементами, состояниями, характеристиками. Такое предварительное, приближенное представление объекта исследования называется концептуальной моделью. Этот этап является основой для последующего формального описания объекта. 2. Формализация операций. На основе содержательного описания определяется и анализируется исходное множество характеристик объекта, выделяются наиболее существенные из них. Затем выделяют управляемые и неуправляемые параметры, вводят символьные обозначения. Определяется система ограничений, строится целевая функция модели. Таким образом, происходит замена содержательного описания формальным (символьным, упорядоченным). 3. Проверка адекватности модели. Исходный вариант модели необходимо проверить по следующим аспектам: 1) все ли существенные параметры включены в модель? 2) нет ли в модели несущественных параметров? 3) правильно ли отражены связи между параметрами? 4) правильно ли определены ограничения на значения параметров? Главным путем проверки адекватности модели исследуемому объекту выступает практика. После предварительной проверки приступают к реализации модели и проведению исследований. Полученные результаты моделирования подвергаются анализу на соответствие известным свойствам исследуемого объекта. По результатам проверки модели на адекватность принимается решение о возможности ее практического использования или о проведении корректировки. 4. Корректировка модели. На этом этапе уточняются имеющиеся сведения об объекте и все параметры построенной модели. Вносятся изменения в модель, и вновь выполняется оценка адекватности. 5. Оптимизация модели. Сущность оптимизации (улучшения) моделей состоит в их упрощении при заданном уровне адекватности. В основе оптимизации лежит возможность преобразования моделей из одной формы в другую. Основными показателями, по которым возможна оптимизация модели, являются время и затраты средств для проведения исследований и принятия решений с помощью модели.

В зависимости от характера и объема априорной информации об объекте исследования выделяют два способа построения моделей систем управления в формах, принятых в теории управления: аналитический и экспериментальный.

Аналитический способ применяется для построения моделей объектов хорошо изученной природы. В этом случае имеется вся необходимая информация о свойствах объекта, но она представлена в другой форме. В результате идеализации физических объектов появляются структурные модели в виде схем с сосредоточенными компонентами. Типичными представителями физических систем, допускающих такое представление, являются электрические и механические объекты.

Подобные схемы являются моделями, в которых информация об интересующих свойствах объекта представлена в наглядной форме с использованием графических образов, отражающих физическую природу явлений, устройство и параметры объектов. На таких моделях базируются соответствующие дисциплины, например, теоретическая электротехника и теоретическая механика. Принципиальные схемы – стационарные линейные модели с сосредоточенными компонентами.

Методы теории управления абстрагируются от конкретной природы объектов и оперируют более общими – математическими (символьными) моделями.

Аналитический способ моделирования складывается из этапа построения схемы объекта и ее дальнейшего преобразования в математическое описание требуемой формы. При этом принципиальные проблемы моделирования решаются на первом – неформальном этапе. Второй этап оказывается процедурой преобразования форм представления моделей. Это дает возможность разработать различные компьютерные программы, позволяющие автоматизировать составление уравнений по схемам.

При моделировании объектов различной природы – электрической, механической поступательной и вращательной, гидравлической или пневматической и др., а также смешанной природы, например электромеханической (двигатели, генераторы), могут быть выделены аналогичные пассивные и активные компоненты. Дальнейшей абстракцией при построении моделей физических объектов с сосредоточенными компонентами является полюсный граф. Эти универсальные топологические модели позволяют унифицировать составление уравнений. Специфика предметной области проявляется только на этапе построения схемы и полюсного графа, а также на заключительном этапе интерпретации результатов анализа и синтеза.

При проектировании систем управления, когда некоторые элементы реально не существуют, аналитический метод построения моделей оказывается единственно возможным.

Если свойства объекта познаны в недостаточной степени, либо происходящие явления слишком сложны для аналитического описания, для построения математических моделей реально существующих объектов применяется экспериментальный способ, который заключается в активных экспериментах над объектом или в пассивной регистрации его поведения в режиме нормальной эксплуатации. В результате обработки данных наблюдений получают модели в требуемой форме. Совокупность этих операций объединяется термином идентификация объекта. В результате идентификации получаются модели вход-выход. Модель зависит не только от свойств объекта, но также от входных сигналов, их разнообразия. Практически об идентифицируемом объекте всегда имеется какая-то априорная информация, т. е. он не является «черным ящиком». Это дает возможность комбинировать оба способа – вначале аналитически строить структуру модели и определять начальные приближенные значения параметров, а далее обработкой экспериментальных данных уточнять их значения.

Основным понятием в области биотехнологических процессов и систем является понятие биотехнологии. Биотехнология – это целенаправленное получение ценных для народного хозяйства и различных областей человеческой деятельности продуктов, в процессе которых используется биохимическая деятельность микроорганизмов, изолированных клеток или их компонентов.

Основываясь на вышесказанном, математическое моделирование любого биотехнологического процесса, аппарата или системы сводится к оценке скорости протекания биохимических процессов, которая определяется скоростью биохимической деятельности (роста) микрообъектов в зависимости от одного или нескольких параметров среды, обеспечивающей протекание метаболических процессов.

В качестве основных видов биохимической деятельности микрообъектов, используемых в биотехнологии, как правило, выступают следующие:

1 Рост клеточной массы биореагентов, которые и представляют собой продукт. К данному классу процессов относится получение пекарских дрожжей в пищевой промышленности, кормовых дрожжей в сельском хозяйстве, вакцин в медицине.

2 Образование (биосинтез) в процессе роста и развития клеток ценных биохимических продуктов– некоторые из которых выделяются в среду (внеклеточные продукты), некоторые накапливаются в биомассе (внутриклеточные продукты). В этих случаях производство существует ради получения таких продуктов, а не самой биомассы, которая часто является балластом.

3 Биотрансформация – процесс, в результате которого под воздействием биологической деятельности микроорганизмов или ферментов происходит изменение химического состава исходного химического вещества. Примером процесса биотрансформации является превращение глюкозы во фруктозу под воздействием фермента глюкоизомеразы или глицерина в диоксиацетон под воздействием глюконобактерий.

4 Потребление микроорганизмами из жидких сред различных веществ, которые являются загрязнителями. В ходе данных процессов биомасса микроорганизмов является промежуточным агентом. Такие процессы применяют при биохимической очистке сточных вод.

5 Выщелачивание с помощью микроорганизмов, т.е. перевод в растворенное состояние некоторых веществ, находящихся в твердых телах. Примером данных процессов является микробиологическое выщелачивание металлов из руд в добывающей и металлургической промышленности.

6 Использование биохимической деятельности микроорганизмов с целью образования газов и за счет этого создания, например, пористых материалов. Данные процессы широко используются в пищевой промышленности при приготовлении хлеба, пива или шампанского.

При математическом описании перечисленных процессов основная задача сводится к оценке реак­ции микрореагентов на различные возмущающие факторы среды. При этом микрореагенты представ­ляют собой весьма сложные объекты, математическое описание которых с традиционных представле­ний применяемых для описания технологических объектов оказывается затруднительным и возможно только на основе обширной системы допущений. В виду этого в последние десятилетия особой попу­лярностью пользуется синергетический подход, разработанный Г. Никольсом и И. Пригожиным для не­равновесных систем в химии и биологии [6]. Другим распространенным методом описания биотехноло­гических микрореагентов является применение геометрических моделей, называемых клеточными ав­томатами.

Клеточные автоматы были впервые рассмотрены фон Нейманом и Уламом в 1948 г. и позднее по­пуляризированы Д. Конвеем в 1970 г. в виде игры «Жизнь». Особенностью клеточных автоматов явля­ется то, что они представляют собой математическую идеализацию биологических систем, в которых пространство и время дискретны, а физические параметры среды принимают конечное множество дис­кретных значений [7].

Указанные математические модели широко используются для описания сложных биологических процессов и систем, примерами которых могут являться: процессы мутации штаммов микроорганизмов, сложные биохимические процессы (например, гликолиз), процессы эволюции экосистем и многие дру­гие.

Однако в большинстве случаев математическое описание биотехнологических процессов может быть решено посредством применения ряда упрощенных моделей. Наиболее часто используемыми яв­ляются математические модели кинетики биотехнологических процессов, построенные по принципу так называемых моделей «черного ящика». В соответствии с этой моделью на входе в объект, который принципиально не рассматривался иначе как линейные или нелинейные регрессионные уравнения или еще как аддитивно-решетчатые, задают значения уровней входных факторов (начальных концентраций компонентов среды), на выходе - непо­средственно значение параметра оптимизации.

Математическое моделирование социально-экономических систем - это теоретико-экспериментальный метод познавательно-созидательной деятельности, это метод исследования и объяснения явлений, процессов и систем (объектов-оригиналов) на основе создания новых объектов - математических моделей. Под математической моделью принято понимать совокупность соотношений (уравнений, неравенств, логических условий, операторов и т.п.), определяющих характеристики состояний объекта моделирования, а через них и выходные значения – реакции, в зависимости от параметров объекта-оригинала, входных воздействий, начальных и граничных условий, а также времени.

Математическая модель, чаще всего, учитывает только те свойства (атрибуты) объекта-оригинала, которые отражают, определяют и представляют интерес с точки зрения целей и задач конкретного исследования. Следовательно, в зависимости от целей моделирования, при рассмотрении одного и того же объекта-оригинала с различных точек зрения и в различных аспектах, последний может иметь различные математические описания, и, как следствие, быть представлен различными математическими моделями. Классификацию видов моделирования и, соответственно, моделей проводят по разным признакам: по сфере приложения (области применения), по характеру моделируемых объектов, по степени подробности моделей и т.д.

Экономико-математические модели отражают наиболее существенные свойства реального объекта или процесса с помощью системы уравнений. Единой классификации экономико-математических моделей также не существует, хотя можно выделить наиболее значимые их группы в зависимости от признака классификации.

По степени агрегирования объектов моделирования различают модели:

• микроэкономические;

• одно-, двухсекторные (одно-, двухпродуктовые);

• многосекторные (многопродуктовые);

• макроэкономические;

• глобальные.

По учету фактора времени различают модели:

 статические;

 динамические.  В статических моделях экономическая система описана в статике, применительно к одному определенному моменту времени. Это как бы снимок, срез, фрагмент динамической системы в какой-то момент времени. Динамические модели описывают экономическую систему в развитии.

По цели создания и применения различают модели:

• балансовые;

• эконометрические;

• оптимизационные;

• сетевые;

• систем массового обслуживания;

• имитационные (экспертные).

В балансовых моделях отражается требование соответствия наличия ресурсов и их использования.  Параметры эконометрических моделей оцениваются с помощью методов математической статистики. Наиболее распространены эконометрические модели, представляющие собой системы регрессионных уравнений. В данных уравнениях отражается зависимость эндогенных (зависимых) переменных от экзогенных (независимых) переменных. Данная зависимость в основном выражается через тренд (длительную тенденцию) основных показателей моделируемой экономической системы. Эконометрические модели используются для анализа и прогнозирования конкретных экономических процессов с использованием реальной статистической информации.  Оптимизационные модели позволяют найти из множества возможных (альтернативных) вариантов наилучший вариант производства, распределения или потребления. Ограниченные ресурсы при этом будут использованы наиболее эффективным образом для достижения поставленной цели.  Сетевые модели наиболее широко применяются в управлении проектами. Сетевая модель отображает комплекс работ (операций) и событий и их взаимосвязь во времени. Обычно сетевая модель предназначена для выполнения работ в такой последовательности, чтобы сроки выполнения проекта были минимальными. В этом случае ставится задача нахождения критического пути. Однако существуют и такие сетевые модели, которые ориентированы не на критерий времени, а, например, на минимизацию стоимости работ.  Модели систем массового обслуживания создаются для минимизации затрат времени на ожидание в очереди и времени простоев каналов обслуживания.  Имитационная модель наряду с машинными решениями содержит блоки, где решения принимаются человеком (экспертом). Вместо непосредственного участия человека в принятии решений может выступать база знаний. В этом случае ЭВМ, специализированное программное обеспечение, база данных и база знаний образуют экспертную систему. Экспертная система предназначена для решения одной или ряда задач методом имитации действий человека, эксперта в данной области.  По учету фактора неопределенности различают модели:

• детерминированные (с однозначно определенными результатами);

• стохастические (с различными вероятностными результатами).

По типу математического аппарата различают модели:

• линейного и нелинейного программирования;

• корреляционно-регрессионные;

• матричные;

• сетевые;

• теории игр;

• теории массового обслуживания и т.д.