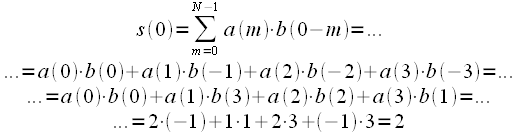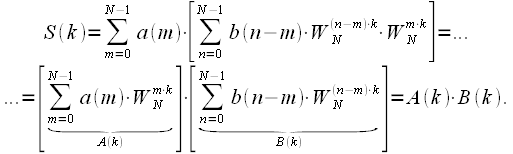10. Основные элементы блок схем программирования, типовые блок схемы (ввода-вывода, исполнения команд, условного перехода; ветвящиеся программы, циклические программы, вложенные циклы).

Алгоритм - это

a. описание последовательности действий для решения задачи или достижения поставленной цели;

b. правила выполнения основных операций обработки данных;

c. описание вычислений по математическим формулам.

Блок-схемой называют графическое представление алгоритма, в котором он изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.

В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий.

Правила выполнения схем определяются следующими документами:

• ГОСТ 19.701-90. Схемы алгоритмов, программ, данных и систем. Условные обозначения и правила выполнения.^[1]

Для программной документации (устарели, заменяются ГОСТ 19.701-90):

• ГОСТ 19.002-80. Схемы алгоритмов и программ. Правила выполнения.^[2]

• ГОСТ 19.003-80. Схемы алгоритмов и программ. Обозначения условные графические.^[3][4]

Данные документы в частности регулируют способы построения схем и внешний вид их элементов.

Основные элементы схем алгоритма:

Наименование	Обозначение	Функция
Блок начало-конец (пуск-остановка)		Элемент отображает вход из внешней среды или выход из неё (наиболее частое применение − начало и конец программы). Внутри фигуры записывается соответствующее действие.
Блок вычислений (вычислительный блок)(процесс)		Выполнение одной или нескольких операций, обработка данных любого вида (изменение значения данных, формы представления, расположения). Внутри фигуры записывают непосредственно сами операции, например, операцию присваивания: a = 10*b + c.
Логический блок (блок условия)		Отображает решение или функцию переключательного типа с одним входом и двумя или более альтернативными выходами, из которых только один может быть выбран после вычисления условий, определенных внутри этого элемента. Вход в элемент обозначается линией, входящей обычно в верхнюю вершину элемента. Если выходов два или три, то обычно каждый выход обозначается линией, выходящей из оставшихся вершин (боковых и нижней). Если выходов больше трех, то их следует показывать одной линией, выходящей из вершины (чаще нижней) элемента, которая затем разветвляется. Соответствующие результаты вычислений могут записываться рядом с линиями, отображающими эти пути. Примеры решения: в общем случае − сравнение (три выхода: >, <, =); в программировании − условные операторы if (два выхода: true, false) и case (множество выходов).
Предопределённый процесс		Символ отображает выполнение процесса, состоящего из одной или нескольких операций, который определен в другом месте программы (в подпрограмме, модуле). Внутри символа записывается название процесса и передаваемые в него данные. Например, в программировании − вызов процедуры или функции.
Данные (ввод-вывод)		Преобразование данных в форму, пригодную для обработки (ввод) или отображения результатов обработки (вывод). Данный символ не определяет носителя данных (для указания типа носителя данных используются специфические символы).
Граница цикла		Символ состоит из двух частей − соответственно, начало и конец цикла − операции, выполняемые внутри цикла, размещаются между ними. Условия цикла и приращения записываются внутри символа начала или конца цикла − в зависимости от типа организации цикла. Часто для изображения на блок-схеме цикла вместо данного символа используют символ условия, указывая в нём решение, а одну из линий выхода замыкают выше в блок-схеме (перед операциями цикла).
Соединитель		Символ отображает вход в часть схемы и выход из другой части этой схемы. Используется для обрыва линии и продолжения её в другом месте (для избежания излишних пересечений или слишком длинных линий, а также, если схема состоит из нескольких страниц). Соответствующие соединительные символы должны иметь одинаковое (при том уникальное) обозначение.
Комментарий		Используется для более подробного описания шага, процесса или группы процессов. Описание помещается со стороны квадратной скобки и охватывается ей по всей высоте. Пунктирная линия идет к описываемому элементу, либо группе элементов (при этом группа выделяется замкнутой пунктирной линией). Также символ комментария следует использовать в тех случаях, когда объём текста, помещаемого внутри некоего символа (например, символ процесса, символ данных и др.), превышает размер самого этого символа.

Блок "процесс" применяется для обозначения действия или последовательности действий, изменяющих значение, форму представления или размещения данных. Для улучшения наглядности схемы несколько отдельных блоков обработки можно объединять в один блок. Представление отдельных операций достаточно свободно.

Блок "решение" используется для обозначения переходов управления по условию. В каждом блоке "решение" должны быть указаны вопрос, условие или сравнение, которые он определяет.

Блок "модификация" используется для организации циклических конструкций. (Слово модификация означает видоизменение, преобразование). Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения.

Блок "предопределенный процесс" используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращений к библиотечным подпрограммам.

Алгоритмы можно представлять как некоторые структуры, состоящие из отдельных базовых (т.е. основных) элементов. Естественно, что при таком подходе к алгоритмам изучение основных принципов их конструирования должно начинаться с изучения этих базовых элементов

Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур: следование, ветвление, цикл.

Характерной особенностью базовых структур является наличие в них одного входа и одного выхода.

1. Базовая структура следование. Образуется из последовательности действий, следующих одно за другим:

2. Базовая структура ветвление. Обеспечивает в зависимости от результата проверки условия (да или нет) выбор одного из альтернативных путей работы алгоритма. Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран.

Структура ветвление существует в четырех основных вариантах:

 если-то;

 если-то-иначе;

 выбор;

 выбор-иначе.

1) если-то

если условие

то действия

конец если

2) если-то-иначе

если условие

то действия 1

иначе действия 2

конец если

3) выбор

выбор

при условие 1: действия 1

при условие 2: действия 2

. . . . . . . . . . . .

при условие N: действия N

конец выбора

4) выбор-иначе

выбор

при условие 1: действия 1

при условие 2: действия 2

. . . . . . . . . . . .

при условие N: действия N

иначе действия N+1

конец выбора

Базовая структура цикл.

Обеспечивает многократное выполнение некоторой совокупности действий, которая называется телом цикла.

Структура цикл существует в трех основных вариантах:

Цикл типа для.

Предписывает выполнять тело цикла для всех значений некоторой переменной (параметра цикла) в заданном диапазоне.

Цикл типа пока.

Предписывает выполнять тело цикла до тех пор, пока выполняется условие, записанное после слова пока.

Цикл типа делать - пока.

Предписывает выполнять тело цикла до тех пор, пока выполняется условие, записанное после слова пока. Условие проверяется после выполнения тела цикла.

Заметим, что циклы для и пока называют также циклами с предпроверкой условия а циклы делать - пока - циклами с постпроверкой условия. Иными словами, тела циклов для и пока могут не выполниться ни разу, если условие окончания цикла изначально не верно. Тело цикла делать - пока выполнится как минимум один раз, даже если условие окончания цикла изначально не верно.

цикл для i от i1 до i2 шаг i3

тело цикла (последовательность действий)

конец цикла

цикл пока условие

тело цикла (последовательность действий)

конец цикла

цикл делать

тело цикла (последовательность действий)

пока условие

конец цикла

Итерационные циклы. Особенностью итерационного цикла является то, что число повторений операторов тела цикла заранее неизвестно. Для его организации используется цикл типа пока. Выход из итерационного цикла осуществляется в случае выполнения заданного условия.

На каждом шаге вычислений происходит последовательное приближение и проверка условия достижения искомого результата.

Пример. Составить алгоритм вычисления суммы ряда

с заданной точностью (для данного знакочередующегося степенного ряда требуемая точность будет достигнута, когда очередное слагаемое станет по абсолютной величине меньше).

Вычисление сумм - типичная циклическая задача. Особенностью же нашей конкретной задачи является то, что число слагаемых (а, следовательно, и число повторений тела цикла) заранее неизвестно. Поэтому выполнение цикла должно завершиться в момент достижения требуемой точности.

При составлении алгоритма нужно учесть, что знаки слагаемых чередуются и степень числа х в числителях слагаемых возрастает.

Решая эту задачу "в лоб" путем вычисления на каждом i-ом шаге частичной суммы

S:=S+(-1)**(i-1)*x**i/i ,

мы получим очень неэффективный алгоритм, требующий выполнения большого числа операций. Гораздо лучше организовать вычисления следующим образом: если обозначить числитель какого-либо слагаемого буквой р, то у следующего слагаемого числитель будет равен -р*х (знак минус обеспечивает чередование знаков слагаемых), а само слагаемое m

будет равно p/i, где i - номер слагаемого.

Алгоритм, в состав которого входит итерационный цикл, называется итерационным алгоритмом. Итерационные алгоритмы используются при реализации итерационных численных методов. В итерационных алгоритмах необходимо обеспечить обязательное достижение условия выхода из цикла (сходимость итерационного процесса). В противном случае произойдет зацикливание алгоритма, т.е. не будет выполняться основное свойство алгоритма - результативность.

Вложенные циклы.

Возможны случаи, когда внутри тела цикла необходимо повторять некоторую последовательность операторов, т. е. организовать внутренний цикл. Такая структура получила название цикла в цикле или вложенных циклов. Глубина вложения циклов (то есть количество вложенных друг в друга циклов) может быть различной.

При использовании такой структуры для экономии машинного времени необходимо выносить из внутреннего цикла во внешний все операторы, которые не зависят от параметра внутреннего цикла.

Пример вложенных циклов для. Вычислить сумму элементов заданной матрицы А(5,3).

Пример вложенных циклов пока. Вычислить произведение тех элементов заданной матрицы A(10,10), которые расположены на пересечении четных строк и четных столбцов.

11.  Алгоритм быстрого преобразования Фурье (алгоритм прямого четырехточечного дискретного преобразования Фурье, алгоритм прямого четырехточечного быстрого преобразования Фурье, сравнение алгоритмов, количество операций сложения и умножения в зависимости от длины преобразуемого массива).

Быстрое преобразование Фурье (БПФ, FFT) — это алгоритм быстрого вычисления дискретного преобразования Фурье (ДПФ). То есть, алгоритм вычисления за количество действий, меньшее чем  , требуемых для прямого (по формуле) вычисления ДПФ. Иногда под БПФ понимается один из быстрых алгоритмов, называемый алгоритмом прореживания по частоте/времени или алгоритмом по основанию 2, имеющего сложность  .

Дискретное преобразование Фурье (в англоязычной литературе DFT, Discrete Fourier Transform) — это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука в MP3, сжатии изображений в JPEG и др.), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. Дискретное преобразование Фурье требует в качестве входа дискретную функцию. Такие функции часто создаются путёмдискретизации (выборки значений из непрерывных функций). Дискретные преобразования Фурье помогают решать частные дифференциальные уравнения и выполнять такие операции, как свёртки. Дискретные преобразования Фурье также активно используются в статистике, при анализе временных рядов. Существуют многомерные дискретные преобразования Фурье.

  Дискретное преобразование Фурье (ДПФ) периодического дискретного сигнала x(n) с периодом N  определяется как

                                    (12.1),

где   - основная частота преобразования (бин ДПФ).

Выражение (12.1) можно переписать в виде

                                                          (12.2),

где                                                                                             (12.3).

Коэффициент W_N называется поворачивающим множителем. Легко показать, что   является периодической функцией с периодом N

                                    (12.4).

Поэтому ДПФ X(k) также является периодической функцией по аргументу k с периодом N.

            Дискретное преобразование Фурье может быть использовано и для представления сигнала x(n) конечной длины N, определенного при n=0,1,…,N-1 и равного нулю вне интервала [0,N-1]. Действительно, такой сигнал можно рассматривать как один период соответствующего периодического сигнала и сипользовать преобразования (12.2). Следует только считать, что вне интнрвала [0,N-1] X(k) и x(n) равны нулю.

            Если сравнить ДПФ конечного дискретного сигнала со спектром этого же сигнала, определяемым выражением

                                                                                 (12.5),

то очевидно, что ДПФ представляет собой N отсчетов спектра, взятых на периоде с интервалом дискретизации по частоте, равным  .

            В случае, когда x(n) является комплексным, при прямом вычислении N-точечного ДПФ нужно выполнить для каждого значения k (N-1) умножений и (N-1) сложений комплексных чисел или 4(N-1) умножений и 2(N-1) сложений действительных чисел. Для всех Nзначений k=0,1,…,N-1 требуется (N-1)² умножений и N(N-1) сложений комплексных чисел. Для больших значений N (порядка нескольких сотен или тысяч) прямое вычисление ДПФ по выражению (12.2) требует выполнения весьма большого числа арифметических операций умножения и сложения, что затрудняет реализацию вычислений в реальном масштабе времени.

            Быстрым преобразованием Фурье (БПФ) называют набор алгоритмов, реализация которых приводит к существенному уменьшению вычислительной сложности ДПФ. Основная идея БПФ состоит в том, чтобы разбить исходный N-отсчетный сигнал x(n) на два более коротких сигнала, ДПФ которых могут быть скомбинированы таким образом, чтобы получить ДПФ исходного N-отсчетного сигнала.

            Так, если исходный N-отсчетный сигнал разбить на два N/2-отсчетных сигнала, то для вычисления ДПФ каждого из них потребуется около (N/2)² комплексных умножений. Тогда для вычисления искомого N-отсчетного ДПФ потребуется порядка 2(N/2)²=N²/2 комплексных умножений , т.е. вдвое меньше по сравнению с прямым вычислением. Операцию разбиения можно повторить, вычисляя вместо (N/2)-отсчетного ДПФ два (N/4)-отсчетных ДПФ и сокращая тем сасым объем вычислений еще в два раза. Выигрыш в два раза является приблизительным, поскольку не учитывается, каким образом из ДПФ меньшего размера образуется искомое N-отсчетное ДПФ.

            Существует большое количество алгоритмов БПФ. Однако все они являются частными случаями единого алгоритма, базирующегося на задаче разбиения одного массива чисел на два. Тот факт, что это можно сделать более чем одним способом, определяет многообразие алгоритмов БПФ. Расмотрим два из них.

            Первый алгоритм называется алгоритмом БПФ с прореживанием по времени.

            Пусть задан N-отсчетный дискретный сигнал x(n). Примем, что N равно степени двойки. Если это не так, то всегда можно легко доплнить заданный сигнал нулевыми отсчетами до количества отсчетов, равного ближайшей степени двойки.

            Разобъем исходный сигнал x(n) на два N/2-отсчетных сигнала x₁(n) и x₂(n), составленных соответственно из четных и нечетных отсчетов исходного сигнала x(n)

                                                              (12.6).

N-точечное ДПФ сигнала x(n) можно записать как

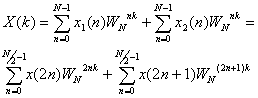                                             (12.7).

С учетом того, что

                                                              (12.8)

можно записать

                                                (12.9)

или

                                                                            (12.10),

где X₁(k) и X₂(k) – N/2-отсчетные ДПФ сигналов x₁(n)  и x₂(n) соответственно.

Таким образом N-точечное ДПФ X(k) может быть разложено на два N/2-точечных ДПФ, результаты которых объединяются согласно (12.10).

            Если бы N/2-точечные ДПФ вычислялись прямым способом, то для вычисления N-точечного ДПФ потребовалось бы (N²/2+N) комплексных умножений. При больших N (когда N²/2>>N) это позволяет сократить время вычислений на 50%.

            Поскольку X(k) определено при  , а X₁(k) и X₂(k) определены при  , необходимо доопределить формулу (12.10) для  . Учитывая, что X₁(k) и X₂(k) – периодические функции с периодомN/2, можно записать

                                     (12.11),

поскольку       .

            Поэтому окончательно для N-точечного ДПФ можно записать

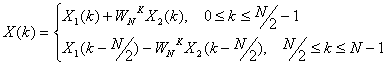                        (12.12).

            На рис.12.1 представлена последовательность операций при выполнении восьмиточечного ДПФ с использованием двух четырехточечных ДПФ.

 

 

 

 

 

 

 

 

 

 

Сначала входной сигнал x(n) разбивается на два сигнала x₁(n) и x₂(n), составленных соответственно из четных и нечетных отсчетов x(n). После этого расчитывается ДПФ X₁(k) и X₂(k). Затем в соответствии с (12.12) получается X(k).

            Рассмотренная схема вычислений может быть использована и для расчета N/2-точечных ДПФ. В соответствии с этим каждый из сигналов x₁(n) и x₂(n) разбиваются на последовательности, состоящие из четных  и нечетных отсчетов родительских сигналов. Аналогично N/2-точечные ДПФ могут быть записаны как комбинации двух N/4-точечных ДПФ

                   (12.13).

С учетом того, что   можно записать

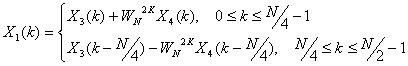                   (12.14).

            На рис.12.2 представлена последовательность операций при выполнении восьмиточечного ДПФ с использованием двух четырехточечных ДПФ и четырех двухточечных ДПФ.

 

 

Таким образом, процесс уменьшения размера ДПФ может быть продолжен, пока не останутся только двухточечные ДПФ, которые могут быть рассчитаны без операции умножения

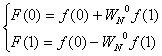                                           (12.15).

Поскольку  , то окончательно получим

                                                                                       (12.16).

На рис.12.3 представлена порядок операций при последовательном вычислении восьмиточечного ДПФ в соответствии с описанным алгоритмом.

 

 

 

 

 

 

 

 

 

 

 

 

 

            Анализ рис.12.3 показывает, что на каждом этапе БПФ необходимо выполнить N/2 комплексных умножений. Поскольку общее количество этапов равно  , то число комплексных умножений, необходимое для нахождения N-точечного ДПФ, приблизительно равно  . Приблизительность оценки означает, что умножения на   в действительности сводятся просто к сложениям и вычитаниям комплексных чисел. Так на первом этапе алгоритма, представленного на рис.12.3, содержатся только сложения и вычитания комплексных чисел поскольку  . Даже на втором этапе используются только сложения и вычитания комплексных чисел т.к.  . Фактически вместо ожидаемых 12 ( ) достаточно выполнить всего два нетривиальных умножения. Однако для больших значений N фактическое число нетривиальных умножений хорошо аппроксимируется выражением  .

            Базовая операция алгоритма с прореживанием по времени (так называемая «бабочка») состоит в том, что два входных числа A и B объединяются для получения двух выходных чисел X и Y по правилу

                                                                                              (12.17).

На рис.12.4 изображен направленный граф базовой операции.

 

 

 

 

 

 

Каждый из этапов ДПФ содержит N/2 базовых операций. В случае когда   - нетривиальный множитель, для каждой базовой операции необходимо выполнить только одно умножение, поскольку величину   можно вычислить и запомнить. Таким образом структура базовых операций такова, что для выполнения БПФ N-отсчетного сигнала, отсчеты которого размещены в памяти, достаточно иметь лишь одну дополнительную ячейку памяти. Результаты всех промежуточных этапов БПФ можно размещать в те же ячейки памяти, где находились исходные данные. Алгоритм БПФ, в котором для размещения входной и выходной последовательности используется один и тот же массив памяти, называется алгоритмом с замещением.

            При реализации алгоритма необходима перестановка отсчетов входного сигнала, чтобы выходная последовательность имела естественный порядок расположения отсчетов, т.е. k=0,1,…,N-1. В приведенном примере для 8-точечного БПФ для этого требовался следующий порядок размещения отсчетов входного сигнала: x(0), x(4), x(2), x(6), x(1), x(5), x(3), x(7). Закономерность перестановки заключается в том, что отсчеты входного сигнала должны быть размещены в памяти в двоично-инверсном порядке. Это означает, что требуемый номер ячейки памяти для размещения очередного отсчета входного сигнала определяется обратной перестановкой двоичных разрядов в двоичном представлении номера отсчета. Для случая N=8 соответствие номеров отсчетов входного сигнала и их номеров ячеек памяти представлено в таблице 12.1.

Номер	Двоичное представление	Двоичная инверсия	Двоично-инверсный порядок
0	000	000	0
1	001	100	4
2	010	010	2
3	011	110	6
4	100	001	1
5	101	101	5
6	110	011	3
7	111	111	7

 

            На рис.12.5 показан алгоритм определения двоично-инверсного номера, предложенный Рейдером. Начиная с первого числа с прямым номером 0, этот алгоритм позволяет формировать последовательно все остальные двоично-инверсные номера.

 

 

Половина из общего числа двоично-инверсных номеров формируются с использованием лишь двух операций, поскольку только в половине случаев старший разряд не равен единице. Аналогично четверть всех двоично-инверсных номеров формируется с использованием трех операций и т.д. таким образом, этот алгоритм является весьма эффективным.

            На всех этапах алгоритма БПФ используются коэффициенты  . Существует несколько способов получения этих коэффициентов. Простейший способ – составление таблицы, к которой можно обращаться в процессе счета. В этом случае для определения коэффициентов не требуется дополнительных вычислений. Однако, для хранения таблицы коэффициентов необходима дополнительная память примерно из N ячеек.

            Второй способ заключается в непосредственном вычислении коэффициентов как

                                                            (12.18)

с использованием процедур вычисления синуса и косинуса. Этот способ связан с большими временными затратами.

            Третий способ основан на применении рекуррентной формулы

                                                                                              (12.19)

с начальным условием  . При вычислении по описываемому алгоритму 16-точечного БПФ на первом этапе используются коэффициенты  , на втором -   , на третьем -  , на четвертом -  . Поэтому, чтобы иметь возможность использовать формулу (12.19) на каждом из этапов, достаточно предварительно вычислить и запомнить коэффициенты  .

            Рассмотрим еще один алгоритм БПФ, который называется алгоритм с прореживанием по частоте.

            Пусть снова имеем входной дискретный сигнал x(n), состоящий из N отсчетов, причем N равно степени двойки. Разобъем это сигнал на два N/2-отсчетных сигнала x₁(n) и x₂(n) так, что x₁(n) состоит из первых N/2 отсчетов x(n), а x₂(n) – из остальных N/2 отсчетов x(n), т.е.

                                                         (12.20).

При таком разбиении N-точечное ДПФ сигнала x(n) можно записать как

                                                          (12.21).

Поскольку  , то получим

                                                          (12.22).

Запишем выражения отдельно для четных и нечетных отсчетов ДПФ.

                                                      (12.23).

Из выражения (12.23) видно, что N-точечное ДПФ можно получить как сумму двух N/2-точечных ДПФ N/2-отсчетных сигналов: сигнала   и сигнала   .

            Аналогично предыдущему алгоритму, описанную процедуру можно применить повторно и представить каждое из N/2-точечных ДПФ в виде комбинации двух N/4-точечных ДПФ и т.д. На рис.12.6 представлен пример 8-точечного БПФ, реализованного по этому алгоритму.

 

 

 

 

 

 

 

 

 

 

 

            Базовая операция этого алгоритма описывается выражением

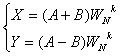                                                                                           (12.24).

            Сравнение двух описанных алгоритмов позволяет выявить два очевидных различия между ними. Во-первых, при прореживании по времени порядок следования входных отсчетов двоично-инверсный, а выходных – прямой. При прореживании по частоте – наоборот. Однако это отличие кажущееся, поскольку в обоих алгоритмах порядок следования входных отсчетов можно сделать прямым. Тогда порядок следования выходных отсчетов будет двоично-инверсным. И наоборот.

            Второе отличие заключается в несколько ином выполеннии базовой операции. При прореживании по частоте комплексное умножение выполняется после сложения-вычитания.

            В обоих алгоритмах для вычисления N-точечного ДПФ требуется около   операций комплексного умножения. Вычисления по обоим алгоритмам могут быть произведены с замещением. В обоих случаях должно быть предусмотрено выполнение двоичной инверсии.

            Обратное ДПФ N-точечной последовательности X(k), k=0,1,…,N-1 определяется как

                                                                                 (12.25).

Взяв выражение, комплексно-сопряженное с (12.25) и умножив его на N получим

                                                                                 (12.26).

Однако, правая часть (12.26) представляет собой прямое ДПФ последовательности X^*(k) и может быть вычислена с использованием одного из вышеописанных алгоритмов БПФ. Искомую последовательность x(n) можно получить, взяв комплексно-сопряженное с (12.26) выражение и разделив его на N

                                                                             (12.27).

Таким образом, алгоритмы БПФ обеспечивают вычисление и прямого и обратного ДПФ.

            Алгоритмы БПФ могут быть использованы для вычисления реакции цифрового фильтра.

            Если на вход фильтра N-го порядка с импульсной характеристикой h(n) подан входной сигнал x(n), то реакция фильтра может быть вычислена по правилу свертки

                                                                                 (12.28).

            Применение алгоритмов БПФ позволяет выполнить эффективное вычисление выходного сигнала y(n) цифрового фильтра. С этой целью следует определить ДПФ H(k) и X(k) в N+M-1 точках для последовательностей h(n) и x(n), затем определить ДПФ Y(k)=X(k)H(k) выходного сигнала y(n). Вычисление y(n) по правилу обратного ДПФ выполняется также с помощью алгоритмов БПФ. Однако, если длина M последовательности x(n) велика, то реализация такого алгоритма вычисления y(n) связана со значительной временной задержкой, необходимой для накопления всех M выборок x(n). С целью уменьшения этой задержки можно входной сигнал x(n) разбить на отрезки x_i(n) каждый длиной L и обрабатывать каждый из нихнезависимо от других. Представим

                                                  (12.29).

Тогда можно (12.28) записать в виде

                                                          (12.30),

где частная свертка y_i(n) определяется как

                                                                               (12.31).

Таким образом можно начинать расчет с помощью алгоритмов БПФ частных сверток и формировать выходной сигнал фильтра y(n) путем соответствующего суммирования элементов частных сверток.

12. Алгоритм фильтрации линейных массивов с помощью операции свертки (алгоритм дискретной фильтрации четырехточечного массива, алгоритм быстрой фильтрации четырехточечного массива с помощью преобразования Фурье).

Одним из китов радиотехники, несомненно, является операция свертки:

(1)

Свертка позволяет рассчитать сигнал   на выходе линейного фильтра с импульсной характеристикой  , при входном сигнале  .

В дискретном случае различают два вида сверток: линейную (или апериодическую) и циклическую. Циклическую свертку еще часто называют круговой или периодической.

Линейная свертка

Рассмотрим линейную свертку. Пусть имеется два дискретных сигнала  , , и  , . В общем случае длины этих сигналов   и   могут отличаться. Линейной сверткой сигналов   и  называется дискретный сигнал вида:

(2)

Для вычисления линейной свертки сигналы  и  сдвигают относительно друг друга почленно перемножают и складывают. При этом предполагается, что   при   и  , а также   при   и 

Графическое представление линейной свертки представлено на рисунке 1.

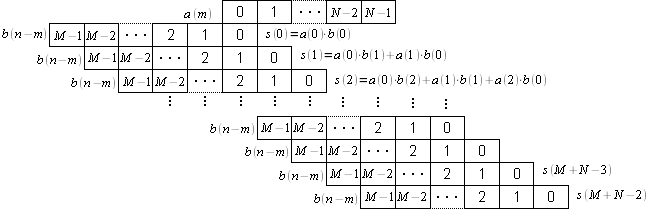  Рисунок 1: Графическое представление линейной свертки

Отсчеты сигнала   сдвигаются относительно отсчетов последовательности   все возможные перекрывающиеся отсчеты почленно перемножаются и складываются.

На рисунке 2 приведен пример вычисления линейной свертки двух сигналов  длиной 4 отсчета и  длиной 3 отсчета.

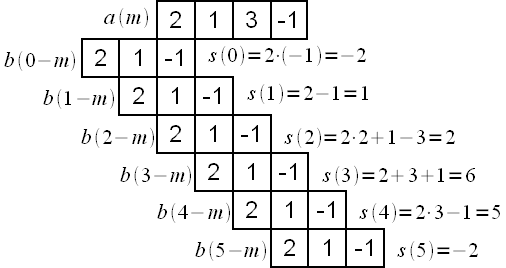  Рисунок 2: Пример вычисления линейной свертки.

Необходимо отметить, что сигнал   при вычислении свертки отражается слева-направо, поскольку  самый первый отсчет (самый ранний по времени) и обрабатываться он также должен первым.

Циклическая свертка

Рассмотрим теперь циклическую свертку. В случае циклической свертки предполагается, что дискретные сигналы  и  - периодические с одинаковым периодом   отсчетов. Тогда круговой сверткой сигналов  и  называется сигнал вида:

(3)

Результат циклической свертки также имеет длину   отсчетов.

Рассмотрим циклическую свертку на примере двух сигналов   и   . Графически вычисление циклической свертки представлено на рисунке 3.

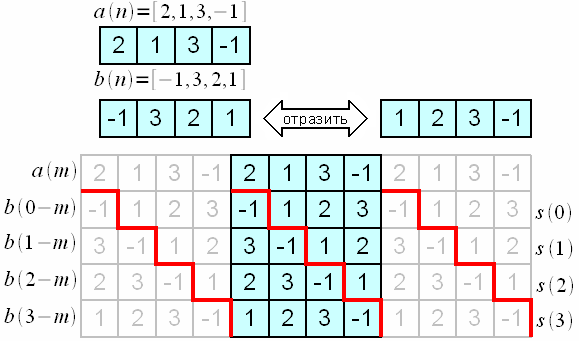  Рисунок 3: Вычисление циклической свертки

Красной линией отмечены границы периодов повторения сигнала  . Заметим, что в силу периодичности сигналов .

Вычислим свертку пошагово:

(4)

Теперь рассчитаем  :

(5)

Аналогично можно рассчитать   и  .

Используя циклическую свертку можно рассчитать линейную свертку двух сигналов. Для этого необходимо каждый из сигналов   и  длительностью  и   отсчетов соответственно дополнить нулями до длины  .

Приведем пример вычисления линейной свертки через циклическую для   длиной 4 отсчета и длиной 3 отсчета (этот пример был рассмотрен выше).

Дополним нулями  и  , так чтобы в каждой последовательности было по 6 отсчетов.

Вычислим циклическую свертку как это показано на рисунке 4.

  Рисунок 4: Вычисление линейной свертки через циклическую <

Можно сравнить с результатом самого первого примера для линейной свертки и убедится в том, что значения совпадают.

Алгоритм быстрого вычисления свертки на основе БПФ

На первый взгляд может показаться, что вычисление линейной свертки через циклическую не имеет смысла, так как не сокращает вычисления. Действительно для вычисления линейной свертки требовалось   умножений,   и   – длины сворачиваемых сигналов, а при вычислении линейной свертки через циклическую   умножений и сложений. Однако рассмотрим дискретное преобразование Фурье от циклической свертки:

(6)

Подставив выражение для циклической свертки получим:

(7)

Поменяем местами операции суммирования:

(8)

Представим множитель   в виде:

(9)

Подставив (9) в (8) получим:

(10)

Таким образом, спектр циклической свертки есть произведение спектров сворачиваемых сигналов, и для ее вычисления может быть применен алгоритм быстрого преобразования Фурье (БПФ). Таким образом схема вычисления циклической свертки может быть представлена на рисунке 5:

  Рисунок 5: Вычисление циклической свертки с применением БПФ

Поскольку эффективные алгоритмы БПФ существуют не для всех длин   , то можно предложить следующий метод вычисления циклической свертки. Исходные последовательности   и   ,   можно дополнить нулями до длины   , поскольку для длин равных целой степени двойки разработаны эффективные алгоритмы БПФ, после этого применяем схему вычисления свертки, представленную на рисунке 5. На выходе получим  ,   , из которого надо взять только первые   отсчетов.

Аналогично можно поступить и при расчете линейной свертки через циклическую.

Рассмотрим пример. Пусть  , а   . Прямое вычисление линейной свертки потребует  (12 миллионов) операций умножения и сложения.

Дополним каждую из последовательностей до 8192 отсчетов нулями и применим алгоритм БПФ с прореживание по времени, тогда на вычисление одного БПФ потребуется   операций комплексного умножения или 428000 операций действительного умножения. Таких блоков БПФ будет всего 3 штуки, плюс надо учесть 8192 комплексных умножений спектров, итого   , что почти в 7.5 раз ниже чем если бы мы считали линейную свертку в лоб.

Выводы

Таким образом, мы рассмотрели два вида дискретных сверток: линейную и циклическую, установили связь между ними. Было показано, что применение БПФ обеспечивает существенное снижение вычислительных операций при вычислении как циклических, так и линейных сверток.

1 Ромащенко В.Н. Принятие решений: ситуации и советы. Киев., 2005. – с. 93.

2 Там же. – с. 98.

3 Иванов А.И., Малявина А.В. Разработка управленческих решений: Учебное пособие. – М.: МАЭП, ИИК «Калита», 2008. – с. 88.

4 Карпов А.В. Структурно-функциональная организация процессов принятия групповых решений / А.В. Карпов // Вопросы психологии. - 2007. - №1. - С. 130-136.

5 Карпов А.В. Структурно-функциональная организация процессов принятия групповых решений / А.В. Карпов // Вопросы психологии. - 2007. - №1. - С. 130-136.

473