3. Интерполирование функций (многочленами Лагранжа; интерполяционная формула Ньютона; интерполяция кубическими сплайнами).

Интерполя́ция, интерполи́рование — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.

Многим из тех, кто сталкивается с научными и инженерными расчётами часто приходится оперировать наборами значений, полученных опытным путём или методом случайной выборки. Как правило, на основании этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Такая задача называется аппроксимацией. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных.

Существует также близкая к интерполяции задача, которая заключается в аппроксимации какой-либо сложной функции другой, более простой функцией. Если некоторая функция слишком сложна для производительных вычислений, можно попытаться вычислить её значение в нескольких точках, а по ним построить, то есть интерполировать, более простую функцию. Разумеется, использование упрощенной функции не позволяет получить такие же точные результаты, какие давала бы первоначальная функция. Но в некоторых классах задач достигнутый выигрыш в простоте и скорости вычислений может перевесить получаемую погрешность в результатах.

Рассмотрим систему несовпадающих точек   ( ) из некоторой области  . Пусть значения функции   известны только в этих точках:

Задача интерполяции состоит в поиске такой функции   из заданного класса функций, что

• Точки   называют узлами интерполяции, а их совокупность — интерполяционной сеткой.

• Пары 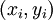  называют точками данных или базовыми точками.

• Разность между «соседними» значениями 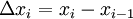  — шагом интерполяционной сетки. Он может быть как переменным, так и постоянным.

• Функцию 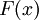  — интерполирующей функцией или интерполянтом.

Аппроксимация функций заключается в приближенной замене заданной функции f(x) некоторой функцией φ(x) так, чтобы отклонение функции φ(x) от f(x) в заданной области было наименьшим. Функция φ(x) при этом на­зывается аппроксимирующей. Типичной задачей аппроксимации функций является задача интерполяции. Необхо­димость интерполяции функций в основном связана с двумя причинами:

1. Функция f(x) имеет сложное аналитическое описание, вызывающее определенные трудности при его ис­пользовании (например, f(x) является спецфункцией: гамма-функцией, эллиптической функцией и др.).

2. Аналитическое описание функции f(x) неизвестно, т. е. f(x) задана таблично. При этом необходимо иметь аналитическое описание, приближенно представляющее f(x) (например, для вычисления значений f(x) в произвольных точках, определения интегралов и производных от f(x) и т. п.)

Постановка задачи интерполяции

Простейшая задача интерполяции заключается в следующем. На отрезке [a, b] заданы п + 1 точки x_i = x₀, x₁, . . ., x_n, которые называются узлами интерполяции, и значения некоторой функции f(x) в этих точках

f(x_o) = y₀, f(x1) = y₁, . . ., f(x_n) = y_n· (1)

Требуется построить функцию Φ(χ) (интерполяционная функция), принадлежащую известному классу и принимающую в узлах интерполяции те же значения, что и f(x), т. е. такую, что

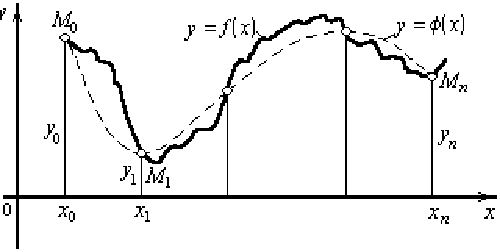
Рисунок 1. Геометрическая интерпретация

Ф(x₀) = y₀, Ф(x₁) = y₁, . . ., Ф(x_n) = y_n· (2)

Геометрически это означает, что нужно найти кривую у = Φ(x) некоторого определенного типа, проходящую через заданную систему точек M(x_i, y_i) (i = 0, 1, ..., п) (Рисунок 1).

В такой общей постановке задача может иметь бесконечное множество решений или совсем не иметь реше­ний.

Однако эта задача становится однозначной, если вместо произвольной функции Φ(x) искать полином¹ φ(x) (интерполяционный полином) степени не выше п, удовлетворяющий условиям (2), т. е. такой, что

φ (x_o) = y₀, φ (x₁) = y₁, . . ., φ (x_n) = y_n· ⁽³⁾

Полученную интерполяционную формулу

φ( x) = a_nxⁿ + a_n-1 x^n-1 +... + a₁ x + a₀ (4)

обычно используют для приближенного вычисления значений данной функции f(x) для значений аргумента x, от­личных от узлов интерполяции. Такая операция называется интерполяцией функций.

Различают два вида интерполяции:

1. глобальная - соединение всех точек f(χ) единым интерполяционным полиномом;

2. локальная - соединение точек отрезками прямой (по двум точкам), отрезками параболы (по трем точкам).

¹ Полиномом (многочленом) или целой рациональной функцией от x, называется функция вида (4), где a₀, a₁, a_n - по­стоянные числа, называемые коэффициентами; п - целое неотрицательное число, называемое степенью полинома.

Интерполяцио́нный многочле́н Лагра́нжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для   пар чисел  , где все   различны, существует единственный многочлен   степени не более  , для которого  .

В простейшем случае ( ) — это линейный многочлен, график которого — прямая, проходящая через две заданные точки.

Лагранж предложил способ вычисления таких многочленов:

где базисные полиномы определяются по формуле:

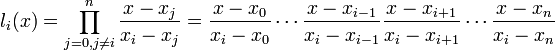
 обладают следующими свойствами:

• являются многочленами степени 

• 

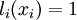
•  при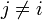 

Отсюда следует, что  , как линейная комбинация  , может иметь степень не больше  , и 

Пример 1

Найдем формулу интерполяции для ƒ(x) = tan(x) имеющей следующие значения:

Получим

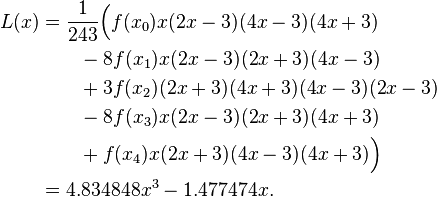
Интерполяционные формулы Ньютона — формулы вычислительной математики, применяющиеся для полиномиального интерполирования.

Если узлы интерполяции равноотстоящие и упорядочены по величине, так что  , то есть  , то интерполяционный многочлен можно записать в форме Ньютона.

Интерполяционные полиномы в форме Ньютона удобно использовать, если точка интерполирования находится вблизи начала (прямая формула Ньютона) или конца таблицы (обратная формула Ньютона).

Пусть для функции   заданы значения   для равноотстоящих значений независимой переменной:  ,  , где   - шаг интерполяции. Требуется подобрать полином   сте­пени не выше  , принимающий в точках   значения

                                                            , .                                             (1)

Условия (1) эквивалентны тому, что    при  .

Интерполяционный полином Ньютона имеет вид:

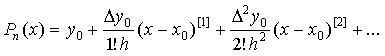
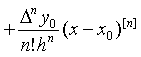.             (2)

Легко видеть, что полином (2) полностью удовлетворяет требованиям поставленной задачи. Действительно, во-первых, степень полинома   не выше  , во-вторых,

   и     ,   .

Заметим, что при   формула (2) превращается в ряд Тейлора для функции  :

.

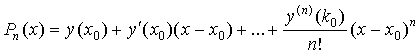    Для практического использования интерполяционную формулу Ньютона (2) обычно записывают в несколько преобразованном виде. Для этого введём новую пере­менную   по формуле     ;   тогда получим:

         ,               (3)

где   представляет собой число шагов, необходимых для достижения точки  , исходя из точки   . Это и есть окончательный вид интерполяционной формулы Ньютона.

     Формулу (3) выгодно использовать для интерполирования функции   в окрестности начального значения  , где   мало по абсолютной величине.

     Если дана неограниченная таблица значений функции  , то число   в интер­поляционной формуле (3) может быть любым. Практически в этом случае число   вы­бирают так, чтобы разность   была постоянной с заданной степенью точности. За начальное значение   можно принимать любое табличное значение аргумента  .

    Если таблица значений функции конечна, то число   ограничено, а именно:   не может быть больше числа значений  функции  , уменьшенного на единицу.

   Заметим, что при применении первой интерполяционной формулы Ньютона удобно пользоваться горизонтальной таблицей разностей, так как тогда нужные значе­ния разностей функции  находятся в соответствующей горизонтальной строке таблицы.

Интерполирование сплайнами

Интерполяционные формулы Лагранжа, Ньютона и Стирлинга и др. при использовании большого числа узлов интерполяции на всем отрезке [a, b] часто приводят к плохому приближению из-за накопления погрешностей в процессе вычислений [2]. Кроме того, из-за расходимости процесса интерполяции увеличение числа узлов не обязательно приводит к повышению точности. Для снижения погрешностей весь отрезок [a, b] разбивается на частичные отрезки и на каждом из них функцию заменяют приближенно полиномом невысокой степени. Это называется кусочно-полиномиальной интерполяцией. 

Один из способов интерполирования на всем отрезке [a, b] является интерполирование сплайнами.

Сплайном называется кусочно-полиномиальная функция, определенная наотрезке [a, b] и имеющая на этом отрезке некоторое количество непрерывных производных. Преимущества интерполяции сплайнами по сравнению с обычными методами интерполяции – в сходимости и устойчивости вычислительного процесса.

Рассмотрим один из наиболее распространенных в практике случаев – интерполирование функции кубическим сплайном. Пусть на отрезке [a, b] задана непрерывная функция . Введем разбиение отрезка:

          (6)

и обозначим   ,  .

Сплайном, соответствующим данной функции и узлам интерполяции (6) называется функция  , удовлетворяющая следующим условиям:

1) на каждом отрезке   ,   функция   является кубическим многочленом;

2) функция  , а также ее первая и вторая производные непрерывны на отрезке [a, b] ;

3) 

Третье условие называется условием интерполирования. Сплайн, определяемый условиями 1) – 3), называется интерполяционным кубическим сплайном.

Рассмотрим способ построения кубического сплайна [2].

На каждом из отрезков  ,  будем искать сплайн-функцию   в виде полинома третьей степени:

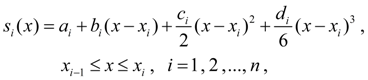          (7)

где  искомые коэффициенты.

Продифференцируем (7) трижды по х :

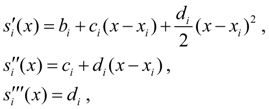
откуда следует

Из условия интерполирования 3) получаем:

.           (8)

Кроме того, будем считать  .

Из условий непрерывности функции  вытекает:

Отсюда с учетом (7) получим:

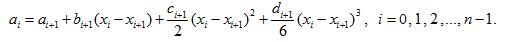
Обозначив и опуская промежуточные выкладки [2], окончательно получим систему уравнений для определения коэффициентов : 

            (9)

В силу трех диагональности матрицы коэффициентов система (9) имеет единственное решение [2]. Найдя коэффициенты   , остальные коэффициенты определим по явным формулам:

              (10)

Таким образом, существует и найден единственный кубический сплайн, удовлетворяющий условиям 1) –  3) .