
- •Основы информационных технологий (теория систем, дискретная и компьютерная математика, теория управления, моделирование) (Первые вопросы в билетах).
- •Интерполирование функций (многочленами Лагранжа; интерполяционная формула Ньютона; интерполяция кубическими сплайнами).
- •Приближение функций (метод наименьших квадратов; линейная регрессия; нелинейная регрессия; полиномиальная аппроксимация; дискретное преобразование Фурье).
- •Формула трапеций
- •Численное решение систем линейных алгебраических уравнений (метод Гаусса; метод итераций).
- •11. Универсальный метод информационных технологий – статистическое моделирование нелинейных систем со случайными характеристиками в условиях помех (метод Монте-Карло).
- •!!!13 И 14 вопросы отсутствуют в билетах!!!
- •!!!16 Вопрос отсутствует в билетах!!!
- •1.2.1. Принцип разомкнутого управления
- •1.2.2. Принцип компенсации
- •1.2.3. Принцип обратной связи
- •1. Введение
- •2. Итерационные методы Якоби и Зейделя
- •3. Метод последовательной верхней релаксации
- •4. Матрично-векторное представление итерационных методов
- •Динамические модели в экономике (регрессионные, авторегрессионные, регрессионно-авторегрессионные модели; модели накопления и дисконтирования; модели «затраты-выпуск»).
- •Основы вычислительной техники. (Вторые вопросы в билетах)
- •Характеристики современных операционных систем (многопоточность, симметричная многопроцессорность, распределенные операционные системы, объектно-ориентированный дизайн).
- •Дискретный сигнал
- •Вычислительные сети и системы (протоколы обмена тср, iр, ssl, skip, NetBeui, ipx, spx, NetBios, модель osi, типы соединения эвм, используемые при построении локальных сетей).
- •Информация (аналоговая и цифровая информация, оценки количества информации, энтропийный подход).
- •Структура микропроцессора (алу, регистры: аккумуляторы, ввода-вывода, понятие шины: шина данных, адресная шина, шина команд; запоминающие устройства: пзу, озу, созу, кэш-память).
- •!!!16 Вопроса нет в билетах!!!
- •17. Понятие нелинейных преобразователей (транзисторы, ключи, диодные выпрямители, логические элементы, нейронные сети).
- •1.8. Основные методы расчета сложных электрических цепей
- •19. Расчет комплексных сопротивлений линейных цепей (последовательные цепи: rc-цепь, rl-цепь, rlc-цепь; параллельные цепи: rc-цепь, rl-цепь, lc-цепь; последовательно-параллельные цепи: r-lc, c-rl).
- •Основы алгоритмизации и программирования. (Третьи вопросы в билетах)
- •2. Методы сортировки и поиска данных в массивах и файлах. Оценки скорости.
- •Современные языки программирования (с, Java, Delphi, vb). Типы данных языка. Структура приложения.
- •Примитивные типы
- •Типы данных
- •Объекты
- •Статическая и динамическая память, определение, область применения. Алгоритмы обработки очереди, списка, стека.
- •4 Шага добавления
- •Основные компоненты в языках (с, Java, Delphi). Их свойства, методы, события. Реализация графики.
- •7. Понятия объектно-ориентированного программирования. Поля, свойства, методы, события. Область видимости. Пример класса.
- •Базы данных. Типы бд. Реляционные бд. Типы полей. Типы связей. Язык запросов sql. Индексирование баз данных.
- •Создание Internet-приложений (на стороне клиента и сервера). Язык разметки гипертекста html. Специализированные инструменты (php). Создание Internet-приложений средствами языков с, Java, Delphi.
- •Глава 1 – содержание элемента html
- •6.3. Рисунки
- •Основные элементы блок схем программирования, типовые блок схемы (ввода-вывода, исполнения команд, условного перехода; ветвящиеся программы, циклические программы, вложенные циклы).
Информация (аналоговая и цифровая информация, оценки количества информации, энтропийный подход).
Информация (от лат. informatio, разъяснение, изложение, осведомленность) — сведения о лицах, предметах, фактах, явлениях, процессах, событиях реального мира независимо от их представления.
В настоящее время не существует единого определения информации как научного термина. С точки зрения различных областей знания данное понятие описывается своим специфическим набором признаков.
Информацию можно разделить на виды по различным критериям:
по способу восприятия:
Визуальная — воспринимаемая органами зрения.
Аудиальная — воспринимаемая органами слуха.
Тактильная — воспринимаемая тактильными рецепторами.
Обонятельная — воспринимаемая обонятельными рецепторами.
Вкусовая — воспринимаемая вкусовыми рецепторами.
по форме представления:
Текстовая — передаваемая в виде символов, предназначенных обозначать лексемы языка.
Числовая — в виде цифр и знаков, обозначающих математические действия.
Графическая — в виде изображений, предметов, графиков.
Звуковая — устная или в виде записи и передачи лексем языка аудиальным путём.
по назначению:
Массовая — содержит тривиальные сведения и оперирует набором понятий, понятным большей части социума.
Специальная — содержит специфический набор понятий, при использовании происходит передача сведений, которые могут быть не понятны основной массе социума, но необходимы и понятны в рамках узкой социальной группы, где используется данная информация.
Секретная — передаваемая узкому кругу лиц и по закрытым (защищённым) каналам.
Личная (приватная) — набор сведений о какой-либо личности, определяющий социальное положение и типы социальных взаимодействий внутри популяции.
по значению:
Актуальная — информация, ценная в данный момент времени.
Достоверная — информация, полученная без искажений.
Понятная — информация, выраженная на языке, понятном тому, кому она предназначена.
Полная — информация, достаточная для принятия правильного решения или понимания.
Полезная — полезность информации определяется субъектом, получившим информацию в зависимости от объёма возможностей её использования.
по истинности:
истинная
ложная
Для информатики основным вопросом является то, каким образом используются средства вычислительной техники для создания, хранения, обработки и передачи информации. В связи с этим информацию классифицируют на аналоговую (непрерывную) и цифровую (дискретную). Человек благодаря своим органам чувств привык иметь дело с аналоговой информацией, а вычислительная техника, наоборот, в основном работает с цифровой информацией.
Человек так устроен, что воспринимает информацию с помощью органов чувств. Свет, звук и тепло - это результат воздействия химических соединений, в основе которого тоже энергетическая природа. Человек испытывает энергетические воздействия непрерывно и может никогда не встретиться с одной и той же их комбинацией дважды. Мы не найдем двух одинаковых зеленых листьев на одном дереве и не услышим двух абсолютно одинаковых звуков - это информация аналоговая. Если же разным цветам дать номера, а разным звукам - ноты, то аналоговую информацию можно превратить в цифровую.
Музыка, когда мы ее слышим, несет аналоговую информацию, но стоит только записать ее нотами, как она становится цифровой.
Разница между аналоговой информацией и цифровой прежде всего в том, что аналоговая информация непрерывна, а цифровая - дискретна.
Преобразование информации из аналоговой формы в цифровую называют аналогово-цифровым преобразованием.
МЕТОДЫ
ОЦЕНКИ КОЛИЧЕСТВА ИНФОРМАЦИИ
Комбинаторный
подход
Пусть
переменное x способно принимать значения,
принадлежащие конечному множеству X,
которое состоит из N элементов. Говорят,
что энтропия переменного равна
![]() Указывая
определенное значение x=a переменного
x, мы «снимаем» эту энтропию, сообщая
информацию
Указывая
определенное значение x=a переменного
x, мы «снимаем» эту энтропию, сообщая
информацию
![]() Если
переменные x1,x2,...,xk способны
независимо пробегать множества, которые
состоят соответственно из
N1,N2,...,Nk элементов,
то
Если
переменные x1,x2,...,xk способны
независимо пробегать множества, которые
состоят соответственно из
N1,N2,...,Nk элементов,
то
![]() Для
передачи количества информации I
приходится употреблять
Для
передачи количества информации I
приходится употреблять
 двоичных
знаков. Например, число различных «слов»,
состоящих из k нулей и единиц и одной
двойки, равно 2k(k
+ 1), поэтому количество информации в
такого рода сообщении равно
двоичных
знаков. Например, число различных «слов»,
состоящих из k нулей и единиц и одной
двойки, равно 2k(k
+ 1), поэтому количество информации в
такого рода сообщении равно
![]() т.е.
для «кодирования» такого рода слов в
чистой двоичной системе требуется
(всюду далее f≈g обозначает, что разность
f-g ограничена, а f~g, что отношение f:g
стремится к единице)
т.е.
для «кодирования» такого рода слов в
чистой двоичной системе требуется
(всюду далее f≈g обозначает, что разность
f-g ограничена, а f~g, что отношение f:g
стремится к единице)
![]() нулей
и единиц.
Посмотрим теперь, в
какой мере чисто комбинаторный подход
позволяет оценить «количество информации»,
содержащееся в переменном x относительно
связанного с ним переменного y. Связь
между переменными x и y, пробегающими
соответственно множества X и Y , заключается
в том, что не все пары x, y, принадлежащие
прямому произведению X.Y , являются
«возможными». По множеству возможных
пар U определяются при любом a
нулей
и единиц.
Посмотрим теперь, в
какой мере чисто комбинаторный подход
позволяет оценить «количество информации»,
содержащееся в переменном x относительно
связанного с ним переменного y. Связь
между переменными x и y, пробегающими
соответственно множества X и Y , заключается
в том, что не все пары x, y, принадлежащие
прямому произведению X.Y , являются
«возможными». По множеству возможных
пар U определяются при любом a![]() X
множества Ya тех
y, для которых (a; y)
U.
X
множества Ya тех
y, для которых (a; y)
U.
x |
y |
|||
1 |
2 |
3 |
4 |
|
1 |
+ |
+ |
+ |
+ |
2 |
+ |
− |
+ |
− |
3 |
− |
+ |
− |
− |
Естественно
определить условную энтропию
равенством
![]() а
информацию в x относительно
y−формулой
а
информацию в x относительно
y−формулой
![]() Например,
в случае, изображенном в таблице
имеем
Например,
в случае, изображенном в таблице
имеем
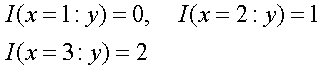 Понятно,
что H(y|x) и I(x:y) являются функциями от x (в
то время как y входит в их обозначение
в виде «связанного переменного»). Без
труда вводится в чисто комбинаторной
концепции представление о «количестве
информации, необходимом для указания
объекта x при заданных требованиях к
точности указания». Очевидно,
Понятно,
что H(y|x) и I(x:y) являются функциями от x (в
то время как y входит в их обозначение
в виде «связанного переменного»). Без
труда вводится в чисто комбинаторной
концепции представление о «количестве
информации, необходимом для указания
объекта x при заданных требованиях к
точности указания». Очевидно,
![]() Вероятностный
подход
Возможности
дальнейшего развития теории информации
на основе определений (5) и (6) остались
в тени ввиду того, что придание переменным
x и y характера «случайных переменных»,
обладающих определенным совместным
распределением вероятностей, позволяет
получить значительно более богатую
систему понятий и соотношений. В параллель
к введенным ранее величинам имеем
здесь
Вероятностный
подход
Возможности
дальнейшего развития теории информации
на основе определений (5) и (6) остались
в тени ввиду того, что придание переменным
x и y характера «случайных переменных»,
обладающих определенным совместным
распределением вероятностей, позволяет
получить значительно более богатую
систему понятий и соотношений. В параллель
к введенным ранее величинам имеем
здесь
![]()
![]()
![]() По-прежнему
HW(y|x)
и IW(x:y)
являются функциями от x. Имеют место
неравенства
По-прежнему
HW(y|x)
и IW(x:y)
являются функциями от x. Имеют место
неравенства
![]() ,
переходящие
в равенства при равномерности
соответствующих распределений (на X и
Yx).
Величины IW(x:y)
и I(x:y) не связаны неравенством определенного
знака.
,
переходящие
в равенства при равномерности
соответствующих распределений (на X и
Yx).
Величины IW(x:y)
и I(x:y) не связаны неравенством определенного
знака.
![]() Но
отличие заключается в том, что можно
образовать математические ожидания
MHW(y|x),
MIW(x:y),
а величина
Но
отличие заключается в том, что можно
образовать математические ожидания
MHW(y|x),
MIW(x:y),
а величина
![]() характеризует
«тесноту связи» между x и y симметричным
образом.
Стоит, однако, отметить
и возникновение в вероятностной концепции
одного парадокса: величина I(x:y) при
комбинаторном подходе всегда
неотрицательна, как это и естественно
при наивном представлении о «количестве
информации», величина же IW(x:y)
может быть и отрицательной. Подлинной
мерой «количества информации» теперь
становится лишь осредненная величина
IW(x,y).
Вероятностный
подход естествен в теории передачи по
каналам связи «массовой» информации,
состоящей из большого числа не связанных
или слабо связанных между собой сообщений,
подчиненных определенным вероятностным
закономерностям. В такого рода вопросах
практически безвредно и укоренившееся
в прикладных работах смешение вероятностей
и частот в пределах одного достаточно
длинного временного ряда (получающее
строгое оправдание при гипотезе
достаточно быстрого «перемешивания»).
Практически можно считать, например,
вопрос об «энтропии» потока поздравительных
телеграмм и «пропускной способности»
канала связи, требующегося для
своевременной и неискаженной передачи,
корректно поставленным в его вероятностной
трактовке и при обычной замене вероятностей
эмпирическими частотами. Если здесь и
остается некоторая неудовлетворенность,
то она связана с известной расплывчатостью
наших концепций, относящихся к связям
между математической теорией вероятностей
и реальными «случайными явлениями
вообще.
Алгоритмический
подход
По
существу, наиболее содержательным
является представление о количестве
информации «в чем-либо (x) и «о чем-либо»
(y). Не случайно именно оно в вероятностной
концепции получило обобщение на случай
непрерывных переменных, для которых
энтропия бесконечна, но в широком круге
случаев конечно.
характеризует
«тесноту связи» между x и y симметричным
образом.
Стоит, однако, отметить
и возникновение в вероятностной концепции
одного парадокса: величина I(x:y) при
комбинаторном подходе всегда
неотрицательна, как это и естественно
при наивном представлении о «количестве
информации», величина же IW(x:y)
может быть и отрицательной. Подлинной
мерой «количества информации» теперь
становится лишь осредненная величина
IW(x,y).
Вероятностный
подход естествен в теории передачи по
каналам связи «массовой» информации,
состоящей из большого числа не связанных
или слабо связанных между собой сообщений,
подчиненных определенным вероятностным
закономерностям. В такого рода вопросах
практически безвредно и укоренившееся
в прикладных работах смешение вероятностей
и частот в пределах одного достаточно
длинного временного ряда (получающее
строгое оправдание при гипотезе
достаточно быстрого «перемешивания»).
Практически можно считать, например,
вопрос об «энтропии» потока поздравительных
телеграмм и «пропускной способности»
канала связи, требующегося для
своевременной и неискаженной передачи,
корректно поставленным в его вероятностной
трактовке и при обычной замене вероятностей
эмпирическими частотами. Если здесь и
остается некоторая неудовлетворенность,
то она связана с известной расплывчатостью
наших концепций, относящихся к связям
между математической теорией вероятностей
и реальными «случайными явлениями
вообще.
Алгоритмический
подход
По
существу, наиболее содержательным
является представление о количестве
информации «в чем-либо (x) и «о чем-либо»
(y). Не случайно именно оно в вероятностной
концепции получило обобщение на случай
непрерывных переменных, для которых
энтропия бесконечна, но в широком круге
случаев конечно.
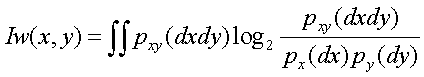 Реальные
объекты, подлежащие нашему изучению,
очень сложны, но связи между двумя
реально существующими объектами
исчерпываются при более простом
схематизированном их описании. Если
географическая карта дает нам значительную
информацию об участке земной поверхности,
то все же микроструктура бумаги и краски,
нанесенной на бумагу, никакого отношения
не имеет к микроструктуре изображенного
участка земной поверхности.
Практически
нас интересует чаще всего количество
информации в индивидуальном объекте x
относительно индивидуального объекта
y. Правда, уже заранее ясно, что такая
индивидуальная оценка количества
информации может иметь разумное
содержание лишь в случаях достаточно
больших количеств информации. Не имеет,
например, смысла спрашивать о количестве
информации в последовательности цифр
0 1 1 0 относительно последовательности
1 1 0 0. Но если мы возьмем вполне конкретную
таблицу случайных чисел обычного в
статистической практике объема и выпишем
для каждой ее цифры цифру единиц ее
квадрата по схеме
Реальные
объекты, подлежащие нашему изучению,
очень сложны, но связи между двумя
реально существующими объектами
исчерпываются при более простом
схематизированном их описании. Если
географическая карта дает нам значительную
информацию об участке земной поверхности,
то все же микроструктура бумаги и краски,
нанесенной на бумагу, никакого отношения
не имеет к микроструктуре изображенного
участка земной поверхности.
Практически
нас интересует чаще всего количество
информации в индивидуальном объекте x
относительно индивидуального объекта
y. Правда, уже заранее ясно, что такая
индивидуальная оценка количества
информации может иметь разумное
содержание лишь в случаях достаточно
больших количеств информации. Не имеет,
например, смысла спрашивать о количестве
информации в последовательности цифр
0 1 1 0 относительно последовательности
1 1 0 0. Но если мы возьмем вполне конкретную
таблицу случайных чисел обычного в
статистической практике объема и выпишем
для каждой ее цифры цифру единиц ее
квадрата по схеме
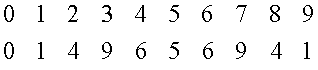 то
новая таблица будет содержать
примерно
то
новая таблица будет содержать
примерно
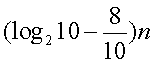 информации
о первоначальной (n - число цифр в
столбцах).
В соответствии с
только что сказанным предлагаемое далее
определение величины IA(x:y)
будет сохранять некоторую неопределенность.
Разные равноценные варианты этого
определения будут приводить к значениям,
эквивалентным лишь в смысле IA1≈IA2,
т.е.
информации
о первоначальной (n - число цифр в
столбцах).
В соответствии с
только что сказанным предлагаемое далее
определение величины IA(x:y)
будет сохранять некоторую неопределенность.
Разные равноценные варианты этого
определения будут приводить к значениям,
эквивалентным лишь в смысле IA1≈IA2,
т.е.
![]() где
константа CA1A2 зависит
от положенных в основу двух вариантов
определения универсальных методов
программирования A1 и
A2.
Будем
рассматривать «нумерованную область
объектов», т.е. счетное множество X={x},
каждому элементу которого поставлена
в соответствие в качестве «номера» n(x)
конечная последовательность нулей и
единиц, начинающаяся с единицы. Обозначим
через l(x) длину последовательности n(x).
Будем предполагать, что:
где
константа CA1A2 зависит
от положенных в основу двух вариантов
определения универсальных методов
программирования A1 и
A2.
Будем
рассматривать «нумерованную область
объектов», т.е. счетное множество X={x},
каждому элементу которого поставлена
в соответствие в качестве «номера» n(x)
конечная последовательность нулей и
единиц, начинающаяся с единицы. Обозначим
через l(x) длину последовательности n(x).
Будем предполагать, что:
соответствие между X и множеством D двоичных последовательностей описанного вида взаимно однозначно;
D
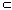 X,
функция n(x) на D общерекурсивна [1], причем
для x
D
X,
функция n(x) на D общерекурсивна [1], причем
для x
D
![]() где
C - некоторая константа;
где
C - некоторая константа;
вместе с x и y в X входит упорядоченная пара (x,y), номер этой пары есть общерекурсивная функция номеров x и y и
![]() где
Cx зависит
только от x.
Не все эти требования
существенны, но они облегчают
изложение.
«Относительной
сложностью» объекта y при заданном x
будем считать минимальную длину l(p)
программы p получения y из x. Сформулированное
так определение зависит от «метода
программирования». Метод программирования
есть не что иное, как функция φ(p,x)=y,
ставящая в соответствие программе p и
объекту x объект y.
В соответствии
с универсально признанными в современной
математической логике взглядами следует
считать функцию φ частично рекурсивной.
Для любой такой функции полагаем
где
Cx зависит
только от x.
Не все эти требования
существенны, но они облегчают
изложение.
«Относительной
сложностью» объекта y при заданном x
будем считать минимальную длину l(p)
программы p получения y из x. Сформулированное
так определение зависит от «метода
программирования». Метод программирования
есть не что иное, как функция φ(p,x)=y,
ставящая в соответствие программе p и
объекту x объект y.
В соответствии
с универсально признанными в современной
математической логике взглядами следует
считать функцию φ частично рекурсивной.
Для любой такой функции полагаем
 При
этом функция υ=φ(u) от u
X
со значениями υ
X
называется частично рекурсивной, если
она порождается частично рекурсивной
функцией преобразования номеров
При
этом функция υ=φ(u) от u
X
со значениями υ
X
называется частично рекурсивной, если
она порождается частично рекурсивной
функцией преобразования номеров
![]() Для
понимания определения важно заметить
что частично рекурсивные функции, вообще
говоря, не являются всюду определенными.
Не существует регулярного процесса для
выяснения того, приведет применение
программы p к объекту x к какому-либо
результату или нет. Поэтому функция
Kφ(y|x)
не обязана быть эффективно вы числимой
(общерекурсивной) даже в случае, когда
она заведомо конечна при любых x и
y.
Основная теорема. Существует
такая частично рекурсивная функция
A(p,x), что для любой другой частично
рекурсивной функции φ(p,x) выполнено
неравенство
Для
понимания определения важно заметить
что частично рекурсивные функции, вообще
говоря, не являются всюду определенными.
Не существует регулярного процесса для
выяснения того, приведет применение
программы p к объекту x к какому-либо
результату или нет. Поэтому функция
Kφ(y|x)
не обязана быть эффективно вы числимой
(общерекурсивной) даже в случае, когда
она заведомо конечна при любых x и
y.
Основная теорема. Существует
такая частично рекурсивная функция
A(p,x), что для любой другой частично
рекурсивной функции φ(p,x) выполнено
неравенство
![]() где
константа Cφ не
зависит от x и y.
Доказательство
опирается на существование универсальной
частично рекурсивной функции Φ(n,u),
обладающей тем свойством, что, фиксируя
надлежащий номер n, можно получить по
формуле φ(u)=Φ(n,u) любую другую частично
рекурсивную функцию. Нужная нам функция
A(p,x) определяется формулой (Φ(n,u)определена
только в случае n
D,A(p,x)
только в случае, когда p имеет вид (n,q),
n
D)
где
константа Cφ не
зависит от x и y.
Доказательство
опирается на существование универсальной
частично рекурсивной функции Φ(n,u),
обладающей тем свойством, что, фиксируя
надлежащий номер n, можно получить по
формуле φ(u)=Φ(n,u) любую другую частично
рекурсивную функцию. Нужная нам функция
A(p,x) определяется формулой (Φ(n,u)определена
только в случае n
D,A(p,x)
только в случае, когда p имеет вид (n,q),
n
D)
![]() В
самом деле, если
В
самом деле, если
![]() то
то
 Функции
A(p,x), удовлетворяющие требованиям
основной теоремы, назовем (как и
определяемые ими методы программирования)
асимптотически оптимальными. Очевидно,
что для них при любых x и y «сложность»
KA(y|x)
конечна. Для двух таких функций A1 и
A2
Функции
A(p,x), удовлетворяющие требованиям
основной теоремы, назовем (как и
определяемые ими методы программирования)
асимптотически оптимальными. Очевидно,
что для них при любых x и y «сложность»
KA(y|x)
конечна. Для двух таких функций A1 и
A2
 Наконец,
KA(y)
= KA(y|1)
можно считать просто «сложностью объекта
y» и определить «количество информации
в x относительно y» формулой
Наконец,
KA(y)
= KA(y|1)
можно считать просто «сложностью объекта
y» и определить «количество информации
в x относительно y» формулой
![]() Легко
доказать (Выбирая в виде функции сравнения
φ(p,x)=A(p,1), получим KA(y|x)≤Kφ(y|x)+Cφ=KA(y)+Cφ),
что величина эта всегда в существенном
положительна:
Легко
доказать (Выбирая в виде функции сравнения
φ(p,x)=A(p,1), получим KA(y|x)≤Kφ(y|x)+Cφ=KA(y)+Cφ),
что величина эта всегда в существенном
положительна:
![]() что
понимается в том смысле, что IA(x:y)
не меньше некоторой отрицательной
константы C, зависящей лишь от условностей
избранного метода программирования.
Как уже говорилось, вся теория рассчитана
на применение к большим количествам
информации, по сравнению с которым |C|
будет пренебрежимо мал.
Наконец,
KA(x|x)≈0,
IA(x:x)≈0;KA(x).
Конечно,
можно избегнуть неопределенностей,
связанных с константами Cφ и
т. д., остановившись на определенных
областях объектов X, их нумерации и
функции A, но сомнительно, чтобы это
можно было сделать без явного произвола.
Следует, однако, думать, что различные
представляющиеся здесь «разумные»
варианты будут приводить к оценкам
«сложностей», расходящимся на сотни, а
не на десятки тысяч бит.
что
понимается в том смысле, что IA(x:y)
не меньше некоторой отрицательной
константы C, зависящей лишь от условностей
избранного метода программирования.
Как уже говорилось, вся теория рассчитана
на применение к большим количествам
информации, по сравнению с которым |C|
будет пренебрежимо мал.
Наконец,
KA(x|x)≈0,
IA(x:x)≈0;KA(x).
Конечно,
можно избегнуть неопределенностей,
связанных с константами Cφ и
т. д., остановившись на определенных
областях объектов X, их нумерации и
функции A, но сомнительно, чтобы это
можно было сделать без явного произвола.
Следует, однако, думать, что различные
представляющиеся здесь «разумные»
варианты будут приводить к оценкам
«сложностей», расходящимся на сотни, а
не на десятки тысяч бит.
ЭНТРОПИЙНЫЙ ПОДХОД
В повседневной жизни мы, как правило, оцениваем полученные сведения со смысловой стороны: новые сведения воспринимаем не как определенное количество информации, а как новое содержание. Есть ли информация в сообщении «на Земле существует растительность»? Конечно, нет. Ведь здесь нет никакого нового содержания. А вот фраза «на Марсе есть растительность» содержит информацию, потому что она отражает вероятность знания, возможность явления, а не утверждает всем известное.
Вот еще один пример. Пассажиры едут в автобусе. Водитель объявляет остановку. Кто-кто выходит, остальные не обращают внимания на слова водителя — переданную им информацию. Почему? Дело в том, что информация здесь имеет разную ценность для получателей, в роли которых в этом примере выступают пассажиры. Вышел тот, для кого информация была ценна. Таким образом,ценность информации – это свойство информации, влияющее на поведение ее получателя.
Как же вычислить количество информации в конкретном сообщении, учитывая его ценность? Такая оценка количества информации основывается на законах теории вероятностей. Это и понятно. Сообщение имеет ценность, несет информацию только тогда, когда мы узнаем из него об исходе события, имеющего случайный характер, когда оно в какой-то мере неожиданно. Ведь сообщение об уже известном никакой информации не содержит.
В теории информации принят так называемый энтропийный подход - подход, который учитывает ценность информации, содержащейся в сообщении для его получателя. Энтропийный подход исходит из следующей модели. Получатель сообщения имеет определенные представления о возможных наступлениях некоторых событий. Эти представления в общем случае недостоверны и выражаются вероятностями, с которыми он ожидает то или иное событие. Общая мера неопределенности – энтропия - характеризуется некоторой математической зависимостью от совокупности этих вероятностей. Количество информации в сообщении определяется тем, насколько уменьшается эта мера после получения сообщения.
Например, тривиальное сообщение, т. е. сообщение о том, что получателю и без того известно, не изменяет ожидаемых вероятностей и не несет для него никакой информации.
Сообщение несет полную информацию о данном множестве событий, если оно целиком снимает всю неопределенность. В этом случае количество информации в нем равно исходной энтропии.
Если вам, допустим, кто-то позвонит по телефону и скажет: «Днем бывает светло, а ночью темно», то такое сообщение вас удивит лишь нелепостью высказывания очевидного и всем известного, а не новостью, которую оно содержит.
Иное дело, например, результат финала в шахматном турнире. Кто выиграет: Карпов или Каспаров? Или партия закончится вничью? Исход здесь трудно предсказать.
И чем больше интересующее нас событие имеет случайных исходов, тем ценнее сообщение о его результате, тем больше информации.
Сообщение о событии, у которого только два одинаково возможных исхода, содержит одну единицу информации, называемую битом. Выбор единицы информации не случаен. Этот выбор, также как и в объемном методе измерения количества информации, связан с наиболее распространенным двоичным способом кодирования при передаче и обработке информации.
Попытаемся хотя бы в самом упрощенном виде представить энтропийный подход к измерению количества информации, который является краеугольным камнем всей теории информации.
Мы уже знаем, что количество информации зависит от вероятностей тех или иных исходов события. Если событие имеет два равновероятных исхода, это означает, что вероятность каждого исхода равна 1/2. Такова вероятность выпадения «орла» или «решки» при бросании монеты. Если событие имеет три равновероятных исхода, как в нашем примере с шахматным турниром, то вероятность каждого равна 1/3. Сумма вероятностей всех исходов всегда равна единице: ведь какой-нибудь из всех возможных исходов обязательно наступит. Событие может иметь и неравновероятные исходы. Так, при футбольном матче между сильной и слабой командами вероятность победы сильной команды велика – например, 4/5. Вероятность ничьей намного меньше, например 3/20. Вероятность же поражения совсем мала.
Рассмотрим классический пример с колодой карт, содержащей 32 различные карты. Чтобы выбрать одну из карт, существует 32 возможности, которые характеризуют исходную неопределенность ситуации. Если при равной вероятности уже выбрана какая-то из них (например, король червей), то неопределенности нет. Таким образом, число 32 в рассматриваемом примере можно было бы считать количеством информации, заложенным в одном выборе из 32 возможностей. Р. Хартли предложил в качестве меры неопределенности логарифм от числа возможностей:
H = k log a m. (1)
Здесь H - количество информации, k - коэффициент пропорциональности, m - число возможных выборов, а - основание логарифма. Чаще всего принимают k=1 и a=2. Тогда стандартной единицей количества информации будет выбор из двух возможностей. Такая единица, как вы уже знаете, носит наименование бита и представляется одним символом двоичного алфавита.
Бит выбран в качестве единицы количества информации потому, что принято считать, что двумя двоичными словами исходной длины m или словом длины 2m можно передать в два раза больше информации, чем одним исходным словом. Число выборов при этом увеличивается в 2m раз, тогда как значение H в соотношении (1) просто удваивается. Интересно, что в соотношении (1) Нхарактеризует число вопросов (двоичных), ответы на которые позволяют выбрать одну из альтернатив. Так, в примере с колодой карт из 32 карт необходимо и достаточно получить ответы «да» и «нет» на пять вопросов (25 = 32). Ответ на каждый вопрос вдвое сокращает область дальнейшего выбора. Пусть, например, необходимо выбрать даму пик. Такими вопросами будут:
1. Карта красной масти? Ответ: «нет».
2. Трефы? Ответ: «нет».
3. Одна из четырех старших? Ответ: «да».
4. Одна из двух старших? Ответ: «нет».
5. Дама? Ответ: «да».
Таким образом, выбрана дама пик. Этот выбор можно описать последовательностью из пяти двоичных символов 00101, в которой 0 соответствует «нет», а 1 соответствует «да».
В данном примере предполагалось, что выборы равновероятны и число их конечно. К. Шеннону принадлежит обобщение H на случай, когда H зависит не только от m, но и от вероятностей выбора символов и вероятностей связей между ними.
Соотношение это выглядит следующим образом:
где Рi - вероятность выбора i-го символа алфавита. Удобнее в качестве меры количества информации пользоваться не значением hi, а средним значением количества информации, приходящейся на один символ алфавита:
Значение H достигает максимума при равенстве всех Рi, т. е. при Рi=1/m. В этом случае последнее соотношение превращается в формулу Р. Хартли (1):
H max = - log P = log m.
Энтропия всегда отрицательна, поскольку величины под знаками логарифмов меньше единицы. По смыслу она противоположна информации, так как информация снимает неопределённость. Поэтому среднее количество информации I в множестве C, т. е. количество информации, приходящееся в среднем на одно сообщение о событии из C, вычисляется по формуле
I(C) = – H(C). (4)
Итак, количество информации есть числовая характеристика сигнала, которая не зависит от его формы и содержания и характеризует степень неопределенности, которая исчезает после выбора (получения) сообщения в виде данного сигнала.
Подведём итог. Информацию можно измерять длиной сообщения в битах. Такой способ ничего не говорит об информативности сообщения, но зато характеризует объём работы системы связи при передаче. Если же в задаче необходимо учитывать информативность, то следует пользоваться энтропийным подходом к измерению информации. При этом нужно уточнить, о каком множестве событий будет сообщаться, каковы их вероятности, после чего вычислить I(C).
