Дискретный сигнал

Дискретизация аналогового сигнала состоит в том, что сигнал представляется в виде последовательности значений, взятых в дискретные моменты времени. Эти значения называются отсчётами. Δt называется интервалом дискретизации.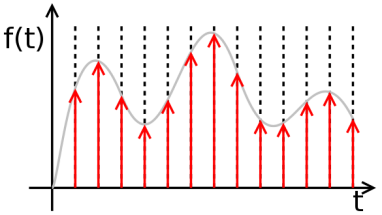

Квантование по уровню - это процесс замены непрерывной функции ее отдельными значениями, отстоящими друг от друга на конечный интервал (уровень). При квантовании значение функции в произвольный момент времени заменяется ее ближайшим значением, называемым уровнем квантования. Интервал между двумя дискретными значениями уровней называется шагом квантования (q).

Квантование по времени Если замена непрерывной функции ее отдельными значениями производится в определенные моменты времени, то этот процесс называется квантованием по времени, или дискретизацией. На рис. а) показано, что горизонтальная ось времени делится на интервалы, отстоящие друг от друга на один и тот же интервал квантования  .

При квантовании по уровню передаваемые значения могут следовать друг за другом с переменным шагом ∆t. При квантовании по времени найденные значения непрерывной величины в дискретные моменты времени чередуются через строго определенные интервалы времени ∆t (шаг квантования), но имеют самую разнообразную амплитуду (уровень).

В некоторых случаях квантование осуществляется с заданными шагами квантования, как по времени, так и по уровню. На рис. а) показано, как производится квантование по уровню и по времени функции  (t). Сначала проводятся линии, параллельные оси   с шагом  t, затем уровни с шагом q, параллельные оси времени. Квантование осуществляется путем замены через время  t значений функции  (t) ближайшим дискретным уровнем. Проследим по рис., как находятся эти точки.

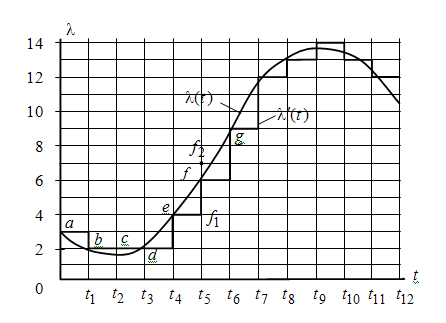
Рис. Квантование по уровню и времени

Амплиту́дная модуляция — вид модуляции, при которой изменяемым параметром несущего сигнала является его амплитуда

Частотная модуляция (ЧМ) — вид аналоговой модуляции, при котором информационный сигнал управляет частотой несущего колебания. По сравнению с амплитудной модуляцией здесь амплитуда остаётся постоянной.

Фазовая модуляция — один из видов модуляции колебаний, при которой фаза несущего колебания управляется информационным сигналом. Фазомодулированный сигнал   имеет следующий вид:

,

где   — огибающая сигнала;   является модулирующим сигналом;   — частота несущего сигнала; t — время.

Фазовая модуляция, не связанная с начальной фазой несущего сигнала, называется относительной фазовой модуляцией (ОФМ).

7. Логические функции, логические элементы, устройства (функции «НЕ», «ИЛИ», «И» и др., таблицы истинности, возможная реализация, условное изображение; структурная схема АЛУ, типы и назначение регистров, используемых в АЛУ)

Логическая функция - это функция логических переменных, которая может принимать только два значения : 0 или 1. В свою очередь, сама логическая переменная (аргумент логической функции) тоже может принимать только два значения : 0 или 1.

Логический элемент - это устройство, реализующее ту или иную логическую функцию.

Y=f(X1,X2,X3,...,Xn) - логическая функция, она может быть задана таблицей, которая называется таблицей истинности.

Число строк в таблице - это число возможных наборов значений аргументов. Оно равно 2ⁿ, где n - число переменных. Число различных функций n переменных равно 2^{2^n}.

Логические функции одной переменной

Таблица истинности функции одной переменной Y=f(X) содержит всего 2 строки, а число функций одной переменной равно 4.

1. Функция константа 0, Y=0. Техническая реализация этой функции - соединение вывода Y с общей шиной с нулевым потенциалом.

Таблица истинности функции константа 0 имеет вид:

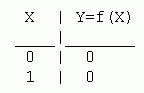
2. Функция Y=f(X)=X - функция повторения. Техническая реализация этой функции - соединение между собой выводов X и Y.

Таблица истинности функции повторения имеет вид:

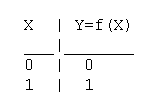
3. Функция Y=f(X)=NOT(X) - отрицание НЕ или инверсия (NOT(X) - это НЕ X).

Техническая реализация этой функции - инвертор на любом транзисторе или логическом элементе, или транзисторный ключ.

Таблица истинности функции отрицания имеет вид:

Логический элемент НЕ обозначается на схемах следующим образом: (пишется X c чертой сверху)

4. Функция константа 1, Y=1. Техническая реализация этой функции - соединение вывода Y с источником питания.

Таблица истинности функции константа 1 имеет вид:

Важнейшей функцией одной переменной является отрицание НЕ, остальные функции являются тривиальными.

Логические функции двух переменных

Таблица истинности функции двух переменных Y=f(X1,Х2) содержит 4 строки, а число функций двух переменных равно 16.

Мы рассмотрим только несколько основных функций двух переменных.

1. Логическое ИЛИ (логическое сложение, дизъюнкция):

Y= X1 + X2 = X1VX2

Техническая реализация этой функции - два параллельно соединенных ключа:

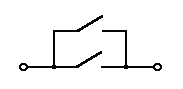
Таблица истинности логического ИЛИ имеет вид:

Логический элемент ИЛИ обозначается на схемах следующим образом:

2. Логическое И (логическое умножение, конъюнкция, схема совпадений): Y = X1X2 = X1&X2

Техническая реализация этой функции - два последовательно соединенных ключа:

Таблица истинности логического И имеет вид:

Логический элемент И обозначается на схемах следующим образом:

3. Функция стрелка Пирса (ИЛИ-НЕ): Y = NOT(X1+X2)

Таблица истинности функции ИЛИ-НЕ имеет вид:

Логический элемент ИЛИ-НЕ обозначается на схемах следующим образом:

4. Функция штрих Шеффера (И-НЕ): Y = X1|X2 = NOT(X1X2)

Таблица истинности функции И-НЕ имеет вид:

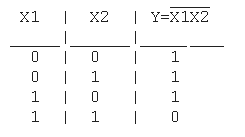
Логический элемент И-НЕ обозначается на схемах следующим образом:

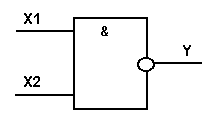
Есть ещё три логические функции двух переменных, имеющие специальные названия: импликация, эквивалентность, неравнозначность (исключающее ИЛИ, сложение по модулю 2). Последние две функции являются взаимно обратными, также как, например, функция И и функция штрих Шеффера.

Элемент памяти - RS-триггер

Триггер - это логическое устройство, способное хранить 1 бит информации. К триггерам относятся устройства, имеющие два устойчивых состояния. Простейший триггер - RS-триггер, образован из двух элементов И-НЕ (или ИЛИ-НЕ). Он позволяет запоминать 1 бит информации, поскольку информация в компьютере представляется в двоичном виде. Его схема приведена ниже.

Действие RS-триггера поясняется в приведенной ниже таблице истинности. S-вход установки (Set), R-вход сброса (Reset).

В обычном (исходном) состоянии на входы триггера поданы 1. Для записи информации на вход R подан 0. Для сброса информации и подготовки к приёму новой информации на вход S подается 0 и триггер вернётся в исходное состояние.

Поскольку один триггер запоминает 1 бит информации, то для запоминания 1 байта (8 бит) нужно 8 триггеров, для запоминания 1 Кб(1024 байт) надо 8192 триггеров. Современные микросхемы ОЗУ способны запоминать тысячи мегабайт информации.

Арифметико-логическое устройство (АЛУ) - центральная часть процессора, выполняющая арифметические и логические операции.

АЛУ реализует важную часть процесса обработки данных. Она заключается в выполнении набора простых операций. Операции АЛУ подразделяются на три основные категории: арифметические, логические и операции над битами. Арифметической операцией называют процедуру обработки данных, аргументы и результат которой являются числами (сложение, вычитание, умножение, деление,...). Логической операцией именуют процедуру, осуществляющую построение сложного высказывания (операции И, ИЛИ, НЕ,...). Операции над битами обычно подразумевают сдвиги.

Разработчик компьютера ENIAC, Джон фон Нейман, был первым создателем АЛУ. В 1945 году он опубликовал первые научные работы по новому компьютеру, названному EDVAC (Electronic Discrete Variable Computer). Годом позже он работал со своими коллегами над разработкой компьютера для Принстонского института новейших исследований (IAS). Архитектура этого компьютера позже стала прототипом архитектур большинства последующих компьютеров. В своих работах фон Нейман указывал устройства, которые, как он считал, должны присутствовать в компьютерах. Среди этих устройств присутствовало и АЛУ. Фон Нейман отмечал, что АЛУ необходимо для компьютера, поскольку оно гарантирует, что компьютер будет способен выполнять базовые математические операции включая сложение, вычитание, умножение и деление.

АЛУ состоит из регистров, сумматора с соответствующими логическими схемами и элемента управления выполняемым процессом. Устройство работает в соответствии с сообщаемыми ему именами (кодами) операций, которые при пересылке данных нужно выполнить над переменными, помещаемыми в регистры.

Арифметико-логическое устройство функционально можно разделить на две части :

1. микропрограммное устройство (устройство управления), задающее последовательность микрокоманд (команд);

2. операционное устройство (АЛУ), в котором реализуется заданная последовательность микрокоманд (команд).

Рисунок 1 - Структурная схема арифметико-логического устройства.

Структурная схема АЛУ и его связь с другими блоками машины показаны на рисунке 1. В состав АЛУ входят регистры Рг1 - Рг7, в которых обрабатывается информация , поступающая из оперативной или пассивной памяти N1, N2, ...NS; логические схемы, реализующие обработку слов по микрокомандам, поступающим из устройства управления.

Закон переработки информации задает микропрограмма , которая записывается в виде последовательности микрокоманд A1,A2, ..., Аn-1,An. При этом различают два вида микрокоманд: внешние, то есть такие микрокоманды, которые поступают в АЛУ от внешних источников и вызывают в нем те или иные преобразования информации (на рис. 1 микрокоманды A1,A2,..., Аn), и внутренние, которые генерируются в АЛУ и воздействуют на микропрограммное устройство, изменяя естественный порядок следования микрокоманд. Например, АЛУ может генерировать признаки в зависимости от результата вычислений: признак переполнения, признак отрицательного числа, признак равенства 0 всех разрядов числа др. На рис. 1 эти микрокоманды обозначены р1, p2,..., рm.

Результаты вычислений из АЛУ передаются по кодовым шинам записи у1, у2, ...,уs, в ОЗУ. Функции регистров, входящих в АЛУ:

• Рг1 - сумматор (или сумматоры) - основной регистр АЛУ, в котором образуется результат вычислений;

• Рг2, РгЗ - регистры слагаемых, сомножителей, делимого или делителя (в зависимости от выполняемой операции);

• Рг4 - адресный регистр (или адресные регистры), предназначен для запоминания (иногда и формирования) адреса операндов и результата;

• Ргб - k индексных регистров, содержимое которых используется для формирования адресов;

• Рг7 - i вспомогательных регистров, которые по желанию программиста могут быть аккумуляторами, индексными регистрами или использоваться для запоминания промежуточных результатов.

Часть операционных регистров является программно-доступной, то есть они могут быть адресованы в команде для выполнения операций с их содержимым. К ним относятся : сумматор, индексные регистры, некоторые вспомогательные регистры.

Остальные регистры программно-недоступные, так как они не могут быть адресованы в программе. Операционные устройства можно классифицировать по виду обрабатываемой информации, по способу обработки информации и логической структуре.

АЛУ может оперировать четырьмя типами информационных объектов: булевскими (1 бит), цифровыми (4 бита), байтными (8 бит) и адресными (16 бит). В АЛУ выполняется 51 различная операция пересылки или преобразования этих данных. Так как используется 11 режимов адресации (7 для данных и 4 для адресов), то путем комбинирования "операция/ режим адресации" базовое число команд 111 расширяется до 255 из 256 возможных при однобайтном коде операции.

Классификация АЛУ

• По способу действия над операндами АЛУ делятся на последовательные и параллельные. В последовательных АЛУ операнды представляются в последовательном коде, а операции производятся последовательно во времени над их отдельными разрядами. В параллельных АЛУ операнды представляются параллельным кодом и операции совершаются параллельно во времени над всеми разрядами операндов.

• По способу представления чисел различают АЛУ:

  1. для чисел с фиксированной точкой;

  2. для чисел с плавающей точкой;

  3. для десятичных чисел.

• По характеру использования элементов и узлов АЛУ делятся на блочные и многофункциональные. В блочном АЛУ операции над числами с фиксированной и плавающей точкой, десятичными числами и алфавитно-цифровыми полями выполняются в отдельных блоках, при этом повышается скорость работы, так как блоки могут параллельно выполнять соответствующие операции, но значительно возрастают затраты оборудования. В многофункциональных АЛУ операции для всех форм представления чисел выполняются одними и теми же схемами, которые коммутируются нужным образом в зависимости от требуемого режима работы.

• По своим функциям АЛУ является операционным блоком, выполняющим микрооперации, обеспечивающие приём из других устройств (например, памяти) операндов, их преобразование и выдачу результатов преобразования в другие устройства. Арифметическо-логическое устройство управляется управляющим блоком, генерирующим управляющие сигналы, инициирующие выполнение в АЛУ определённых микроопераций. Генерируемая управляющим блоком последовательность сигналов определяется кодом операции команды и оповещающими сигналами.

Операции в АЛУ

Выполняемые в АЛУ операции можно разделить на следующие группы:

• операции двоичной арифметики для чисел с фиксированной точкой;

• операции двоичной (или шестнадцатеричной) арифметики для чисел с плавающей точкой;

• операции десятичной арифметики;

• операции индексной арифметики (при модификации адресов команд);

• операции специальной арифметики;

• операции над логическими кодами (логические операции);

• операции над алфавитно-цифровыми полями.

Современные ЭВМ общего назначения обычно реализуют операции всех приведённых выше групп, а малые и микроЭВМ, микропроцессоры и специализированные ЭВМ часто не имеют аппаратуры арифметики чисел с плавающей точкой, десятичной арифметики и операций над алфавитно-цифровыми полями. В этом случае эти операции выполняются специальными подпрограммами. К арифметическим операциям относятся сложение, вычитание, вычитание модулей («короткие операции») и умножение и деление («длинные операции»). Группу логических операций составляют операции дизъюнкция (логическое ИЛИ) и конъюнкция (логическое И) над многоразрядными двоичными словами, сравнение кодов на равенство. Специальные арифметические операции включают в себя нормализацию, арифметический сдвиг (сдвигаются только цифровые разряды, знаковый разряд остаётся на месте), логический сдвиг (знаковый разряд сдвигается вместе с цифровыми разрядами). Обширна группа операций редактирования алфавитно-цифровой информации

8. Системы счисления (принцип построения позиционной системы счисления, основание системы счисления, перевод чисел из одной системы счисления в другую, представление чисел в формате с фиксированной и с плавающей запятой. понятие нормализации, выполнение арифметических действий в двоичной системе счисления над числами в форме с фиксированной и с плавающей запятой).

Система счисления — символический метод записи чисел, представление чисел с помощью письменных знаков.

Системы счисления подразделяются на позиционные и непозиционные, а позиционные, в свою очередь, — на однородные и смешанные. Непозиционная — самая древняя, в ней каждая цифра числа имеет величину, не зависящую от её позиции (разряда). То есть, если у вас 5 черточек — то число тоже равно 5, поскольку каждой черточке, независимо от её места в строке, соответствует всего 1 один предмет. Другим примером непозиционной системы счисления является римская система, использующая набор следующих символов: I, X, V, L, C, D, M и т.д. В этой системе существует отклонение от правила независимости значения цифры от положения в числе. В числах LX и XL символ X принимает два различных значения : +10 - в первом случае и -10 - во втором.  Позиционная система — значение каждой цифры зависит от её позиции (разряда) в числе. Например, привычная для нас 10-я система счисления — позиционная. Рассмотрим число 453. Цифра 4 обозначает количество сотен и соответствует числу 400, 5 — кол-во десяток и аналогично значению 50, а 3 — единиц и значению 3. Как видим — чем больше разряд — тем значение выше. Итоговое число можно представить, как сумму 400+50+3=453. Однородная система — для всех разрядов (позиций) числа набор допустимых символов (цифр) одинаков. В качестве примера возьмем упоминавшуюся ранее 10-ю систему. При записи числа в однородной 10-й системе вы можете использовать в каждом разряде исключительно одну цифру от 0 до 9, таким образом, допускается число 450 (1-й разряд — 0, 2-й — 5, 3-й — 4), а 4F5 — нет, поскольку символ F не входит в набор цифр от 0 до 9. Смешанная система — в каждом разряде (позиции) числа набор допустимых символов (цифр) может отличаться от наборов других разрядов. Яркий пример — система измерения времени. В разряде секунд и минут возможно 60 различных символов (от «00» до «59»), в разряде часов – 24 разных символа (от «00» до «23»), в разряде суток – 365 и т. д.

В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая – 7 единиц, а третья – 7 десятых долей единицы.

Сама же запись числа 757,7 означает сокращенную запись выражения

700 + 50 + 7 + 0,7 = 7•10² + 5•10¹ + 7•10⁰ + 7•10^-1 = 757,7.

    Любая позиционная система счисления характеризуется своим основанием.

   Основание позиционной системы счисления — это количество различных знаков или символов, используемых для изображения цифр в данной системе.

    За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д. Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения

a_n-1 q^n-1 + a_n-2 q^n-2 + ... + a₁ q¹ + a₀ q⁰ + a_-1 q^-1 + ... + a_-m q^-m,

где a_i – цифры системы счисления; n и m – число целых и дробных разрядов, соответственно.

Кроме десятичной широко используются системы с основанием, являющимся целой степенью числа 2, а именно:

• двоичная (используются цифры 0, 1);

• восьмеричная (используются цифры 0, 1, ..., 7);

• шестнадцатеричная (для первых целых чисел от нуля до девяти используются цифры 0, 1, ..., 9, а для следующих чисел — от десяти до пятнадцати – в качестве цифр используются символы A, B, C, D, E, F).

    Из всех систем счисления особенно проста и поэтому интересна для технической реализации в компьютерах двоичная система счисления.

Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.

    Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.

    Компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:

• для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;

• представление информации посредством только двух состояний надежно и помехоустойчиво;

• возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;

• двоичная арифметика намного проще десятичной.

    Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.

Перевод из одной системы счисления в другую.

Для перевода целых чисел из одной системы счисления с основанием S в другую с основанием S1 надо это число последовательно делить на основание S1 новой системы счисления до тех пор, пока не получится частное меньше S1. Число в новой системе запишется в виде остатков деления, начиная с последнего. Это последнее частое дает цифру старшего разряда в новой системе счисления. Деление выполняют в исходной системе счисления. Например:

37710=1011110012

1. Для перевода чисел из любой системы счисления в десятичную необходимо:

А) Старшую цифру исходного числа умножить на основание старой системы счисления и прибавить следующую цифру исходного числа

Б)Результат опять умножить на основание старой системы счисления и прибавить следующую цифру исходного числа

В) Процесс перевода заканчивается после прибавления последней самой младшей цифры исходного числа

2. Для перевода чисел из десятичной системы счисления в любую необходимо делить исходное число на основание новой системы счисления до тех пор пока последнее частное не станет меньше основания новой системы счисления. Результат складывается из остатков деления, начиная с последнего.

3. Для перевода чисел из любой системы счисления в любую необходимо исходное число перевести в десятичную систему по первому правилу (умножением), полученное десятичное число перевести в искомую систему по второму правилу (деление).

4. Для перевода чисел из систем счисления, которые являются степенью двойки необходимо:

А) из 16-ричной в 2-ичную: для перевода 16-ричного числа в двоичную систему необходимо каждую цифру 16-ричного числа заменить 4-х разрядным двоичным значением.

Б) из 8-ричной в 2-ичную: Каждую цифру 8-ричного числа необходимо заменить 3-х разрядным двоичным значением.

Представление чисел с фиксированной и плавающей запятой

В вычислительных машинах применяются две формы представления двоичных чисел:

□ естественная форма или форма с фиксированной запятой (точкой);

□ нормальная форма или форма с плавающей запятой (точкой).

1). В форме представления с фиксированной запятой все числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной.

Например: в десятичной системе счисления имеется 5 разрядов в целой части числа (до запятой) и 5 разрядов в дробной части числа (после запятой); числа имеют вид: +00721,35500; -10301,20260.

Эта форма наиболее проста, естественна, но имеет небольшой диапазон представления чисел и поэтому чаще всего неприемлема при вычислениях. Диапазон значащих чисел N в системе счисления с основанием Р при наличии m разрядов в целой части и s разрядов в дробной части числа (без учета знака числа) будет: . Например, при Р=2, m = 10 и s = 6 диапазон: 0,015 < N < 1024.

Если в результате операции получится число, выходящее за допустимый диапазон, происходит переполнение разрядной сетки, и дальнейшие вычисления теряют смысл. В современных компьютерах естественная форма представления используется как вспомогательная и только для целых чисел.

2). В форме плавающей запятой каждое число изображается в виде двух групп цифр. Первая группа цифр называется мантиссой, вторая — порядком, причем абсолютная величина мантиссы должна быть меньше 1, а порядок — целым числом. В общем виде число в форме с плавающей запятой может быть представлено так: где М — мантисса (|М| < 1); r — порядок (целое); Р — основание системы счисления.

Например, числа запишутся так: +0,721355 • 10³; 0,103012026 • 10⁵.

Нормальная форма представления имеет огромный диапазон отображения чисел и является основной в современных компьютерах. Так, диапазон значащих чисел в системе счисления с основанием Р при наличии m разрядов у мантиссы и s разрядов у порядка (без учета знаковых разрядов порядка и мантиссы) будет:

Приведем пример. При P=2, m=22 и s=10 диапазон чисел простирается примерно от 10^-300 до 10³⁰⁰. Для сравнения: количество секунд, которые прошли с момента образования планеты Земля, составляет всего 10¹⁸. Для m=10 наибольшее число ~ 9,2*10¹⁸.

Следует заметить, что все числа с плавающей запятой хранятся в машине в так называемом нормализованном виде. Нормализованным называют такое число, в старшем разряде мантиссы которого стоит ноль. У нормализованных двоичных чисел, следовательно, 0,5 <= \М\ < 1.

Алгебраическое представление двоичных чисел

Знак числа кодируется двоичной цифрой:

● код 0 означает знак + (плюс), ● код 1 означает знак — (минус).

Для алгебраического представления чисел, то есть для представления чисел с учетом их знака, в машинах используются специальные коды:

□ прямой код числа;

□ обратный код числа;

□ дополнительный код числа.

При этом два последних кода позволяют заменить неудобную для компьютера операцию вычитания на операцию сложения с отрицательным числом.

Дополнительный код обеспечивает более быстрое выполнение операций, поэтому в компьютере применяется чаще именно он.

1). Прямой код числа N обозначим [N]_np.

Пусть модуль N= aaa...а;

□ если N > 0, то [N]_np = 0,ааа...а;

□ если N < 0, то [N]_np = 1,ааа...а;

□ если N = 0, то имеет место неоднозначность: может [0]_np = 0,0... или [0]_np = 1,0...

Если при сложении оба слагаемых имеют одинаковый знак, то операция сложения выполняется обычным путем. Если при сложении слагаемые имеют разные знаки, то сначала необходимо выявить число, большее по абсолютной величине, произвести из него вычитание меньшего числа, а разности присвоить знак большего числа.

Операции умножения и деления в прямом коде выполняются обычным образом, но знак результата определяется по совпадению или не совпадению знаков, участвовавших в операции чисел.

Операцию вычитания в этом коде нельзя заменить операцией сложения с отрицательным числом, поэтому возникают сложности, связанные с заемом значений из старших разрядов уменьшаемого. В связи с этим прямой код в ПК почти не применяется.

2). Обратный код числа N обозначим [N]_обр.

Символ а* означает величину, обратную а, то есть если а = 1, то а* = 0, и наоборот.

□ если N > 0, то [N]_обр = [N]_пр = 0,аа...а,

□ если N < 0, то [N]_обр = 1,а*а*...а*,

Т.е., для того чтобы получить обратный код отрицательного числа, необходимо все цифры этого числа инвертировать (в знаковом разряде поставить 1, во всех значащих разрядах нули заменить единицами, а единицы нулями).

□ если N = 0, то неоднозначность: может [0]_обр = 0,00...0 или [0]_обр = 1,11...1.

Например, число N = 0,1011, тогда [N]_обр = 0,1011. Число N = -0,1011, [N]_обр = 1,0100.

3. Дополнительный код числа N обозначим [N]_доп

□ если N >= 0, то [N]_доп = [N]_пр = 0,аа...а,

□ если N <= 0, то [N]_доп = 1,а*а*...а* + 0,00...1.

Для того чтобы получить дополнительный код отрицательного числа, необходимо все его цифры инвертировать (в знаковом разряде поставить единицу, во всех значащих разрядах нули заменить единицами, а единицы нулями) и затем к младшему разряду прибавить единицу. В случае возникновения переноса из первого после запятой разряда в знаковый разряд, к числу следует прибавить единицу в младший разряд.

Например, если N = 0,1011, то [N]_доп = 0,1011;

N = -0,1100, то [N]_доп = 1,0100;

N = -0,0000, то [N]_доп = 10,0000 = 0,0000 (1-ца исчезает).

Таким образом, неоднозначности в изображении 0 (нуля) в данном случае нет.

Эмпирическое правило: для получения дополнительного кода отрицательного числа необходимо все символы этого числа инвертировать, кроме последней (младшей) единицы и тех нулей, которые за ней следуют.

Правила выполнения арифметических операций в двоичной системе счисления аналогичны правилам операций в десятичной системе счисления.

Особенности выполнения операций над числами с плавающей запятой

Кратко остановимся на выполнении операции над числами с плавающей запятой.

При сложении (вычитании) чисел с одинаковыми порядками их мантиссы складываются (вычитаются), а результату присваивается порядок, общий для исходных чисел.

Если порядки исходных чисел разные, то сначала эти порядки выравниваются (число с меньшим порядком приводится к числу с большим), затем выполняется операция сложения (вычитания) порядков.

Если при выполнении операции сложения мантисс возникает переполнение, то сумма мантисс сдвигается вправо на один разряд, а порядок суммы увеличивается на 1.

При умножении чисел с плавающей запятой их мантиссы перемножаются, а порядки складываются.

При делении числа с плавающей запятой мантисса делимого делится на мантиссу делителя, а для получения порядка частного из порядка делимого вычитается порядок делителя.

Если при этом мантисса делимого больше мантиссы делителя, то мантисса частного окажется больше 1 (происходит переполнение) и ее следует сдвинуть на 1 разряд вправо, одновременно увеличив на единицу порядок частного.

Выполнение арифметических операций над числами в дополнительных кодах

При выполнении арифметических операций в компьютере обычно применяются не простые, а модифицированные коды. Модифицированный код отличается от простого использованием для изображения знака числа двух разрядов.

Второй знаковый разряд служит для автоматического обнаружения ситуации переполнения разрядной сетки: при отсутствии переполнения оба знаковых разряда должны иметь одинаковые цифры (нули или единицы), а при переполнении разрядной сетки цифры в них будут разные. При переполнении результат сдвигается вправо на один разряд.

Сложение производится по обычным правилам сложения двоичных чисел: единица переноса, возникающая из старшего знакового разряда, просто отбрасывается.

Примеры сложения:

X=-­­0,1101; Y=0,1001. Результат сложения: 11,0011 + 00,1001 = 11,1101 (или -1100);

Х= 0,1101; Y=0,1001. Результат сложения: 00,1101 + 00,1001 = 01,0110 (переполнение, после сдвига вправо получим 00,10110, или +10110);

Х= 0,1101; Y=-0,1001. Результат сложения: 00,1101 + 11,0111 = 100,0100(или 00,0100);

X=-0,1101; Y=-0,1001. Результат сложения: 11,0011 + 11,0111 = 110,1010 (переполнение, после сдвига вправо получим 11,01010, или -10110).

Умножение чисел в дополнительных кодах производится по обычным правилам умножения двоичных чисел. Единственной особенностью является то, что если сомножитель является отрицательным (знаковые разряды равны 11), то перед началом умножения следует приписать к нему слева столько единиц, сколько значащих разрядов у другого сомножителя справа от запятой. Результат (произведение) всегда получаем в дополнительном коде.

ПРИМЕЧАНИЕ

Добавление единиц слева перед отрицательным числом не изменяет его величины, так как перед положительным числом можно написать сколь угодно нулей не изменяя величины числа; наоборот, перед отрицательным числом (в дополнительном или обратном кодах) добавление лишних нулей недопустимо.

Примеры операции умножения:

Особенности выполнения операций в обратных кодах

Обратные коды следует складывать как обычные двоичные числа, поступая со знаковыми разрядами, как с обычными разрядами, а если возникает единица переноса из знакового разряда, ее следует прибавить к младшему разряду суммы кодов.

Последнее обстоятельство (возможное добавление единицы в младший разряд) увеличивает время выполнения операций в обратных кодах, поэтому в компьютере чаще используются дополнительные коды.

Выполнение арифметических операций в 16-ричной системе счисления

Арифметические операции в шестнадцатеричной системе в машине не выполняются.

Операции сложения и вычитания чисел в таком представлении иногда приходится выполнять при программировании, например при вычислении полных адресов ячеек памяти (при сложении и вычитании адресов сегмента, базы, индекса, смещения в ПК).

Правила их выполнения - обычные для позиционной системы счисления.

9. Кодирование информации (наименьшие единицы представления, обработки (передачи) и хранения информации, понятия: бит, байт, файл, принципы оптимального кодирования информации с исправлением ошибок, кодирование текстовой информации в ЭВМ, кодирование цветовой информации в ЭВМ)

Слово «информация» в переводе с латинского означает сведения, разъяснения, изложение.

Информацией называются сведения об объектах и явлениях окружающего мира, их свойствах, характеристиках и состоянии, воспринимаемые информационными системами. Информация является характеристикой не сообщения, а соотношения между сообщением и его анализатором. Если отсутствует потребитель, хотя бы потенциальный, говорить об информации не имеет смысла.

В информатике под информацией понимают некоторую последовательность символических обозначений (букв, цифр, образов и звуков и т. п.), которые несут смысловую нагрузку и представлены в понятном для компьютера виде. Все эти виды информации в компьютере представлены в двоичном коде, т. е. используется алфавит мощностью два (всего два символа 0 и 1). Связано это с тем, что удобно представлять информацию в виде последовательности электрических импульсов: импульс отсутствует (0), импульс есть (1). Такое кодирование принято называть двоичным, а сами логические последовательности нулей и единиц - машинным языком.

Кодирование информации — процесс преобразования сигнала из формы, удобной для непосредственного использования информации, в форму, удобную для передачи, хранения или автоматической переработки.

Кодирование информации применяют для унификации формы представления данных, которые относятся кразличным типам, в целях автоматизации работы с информацией.

Кодирование – это выражение данных одного типа через данные другого типа. Например, естественные человеческие языки можно рассматривать как системы кодирования понятий для выражения мыслей посредством речи, к тому же и азбуки представляют собой системы кодирования компонентов языка с помощью графических символов.

В вычислительной технике применяется двоичное кодирование. Основой этой системы кодирования является представление данных через последовательность двух знаков: 0 и 1. Данные знаки называются двоичными цифрами (binary digit), или сокращенно bit (бит). Одним битом могут быть закодированы два понятия: 0 или 1 (да или нет, истина или ложь и т. п.). Двумя битами возможно выразить четыре различных понятия, а тремя – закодировать восемь различных значений.

Наименьшая единица кодирования информации в вычислительной технике после бита – байт. Его связь с битом отражает следующее отношение: 1 байт = 8 бит = 1 символ.

Обычно одним байтом кодируется один символ текстовой информации. Исходя из этого для текстовых документов размер в байтах соответствует лексическому объему в символах.

Более крупной единицей кодирования информации служит килобайт, связанный с байтом следующим соотношением: 1 Кб = 1024 байт.

Другими, более крупными, единицами кодирования информации являются символы, полученные с помощью добавления префиксов мега (Мб), гига (Гб), тера (Тб):

1 Мб = 1 048 580 байт;

1 Гб = 10 737 740 000 байт;

1 Тб = 1024 Гб.

Файл (англ. file) — блок информации на внешнем запоминающем устройстве компьютера, имеющий определённое логическое представление (начиная от простой последовательности битов или байтов и заканчивая объектом сложной СУБД), соответствующие ему операции чтения-записи и, как правило, фиксированное имя (символьное или числовое), позволяющее получить доступ к этому файлу и отличить его от других файлов.

Для кодирования двоичным кодом целого числа следует взять целое число и делить его пополам до тех пор, пока частное не будет равно единице. Совокупность остатков от каждого деления, которая записывается справа налево вместе с последним частным, и будет являться двоичным аналогом десятичного числа.

В процессе кодирования целых чисел от 0 до 255 достаточно использовать 8 разрядов двоичного кода (8 бит). Применение 16 бит позволяет закодировать целые числа от 0 до 65 535, а с помощью 24 бит – более 16,5 млн различных значений.

Для того чтобы закодировать действительные числа, применяют 80-разрядное кодирование. В этом случае число предварительно преобразовывают в нормализованную форму, например:

2,1427926 = 0,21427926 ? 101;

500 000 = 0,5 ? 106.

Первая часть закодированного числа носит название мантиссы, а вторая часть – характеристики. Основная часть из 80 бит отводится для хранения мантиссы, и некоторое фиксированное число разрядов отводится для хранения характеристики.

Текстовую информацию кодируют двоичным кодом через обозначение каждого символа алфавита определенным целым числом. С помощью восьми двоичных разрядов возможно закодировать 256 различных символов. Данного количества символов достаточно для выражения всех символов английского и русского алфавитов.

В первые годы развития компьютерной техники трудности кодирования текстовой информации были вызваны отсутствием необходимых стандартов кодирования. В настоящее время, напротив, существующие трудности связаны с множеством одновременно действующих и зачастую противоречивых стандартов.

Для английского языка, который является неофициальным международным средством общения, эти трудности были решены. Институт стандартизации США выработал и ввел в обращение систему кодирования ASCII (American Standard Code for Information Interchange – стандартный код информационного обмена США).

Для кодировки русского алфавита были разработаны несколько вариантов кодировок:

1) Windows-1251 – введена компанией Microsoft; с учетом широкого распространения операционных систем (ОС) и других программных продуктов этой компании в Российской Федерации она нашла широкое распространение;

2) КОИ-8 (Код Обмена Информацией, восьмизначный) – другая популярная кодировка российского алфавита, распространенная в компьютерных сетях на территории Российской Федерации и в российском секторе Интернет;

3) ISO (International Standard Organization – Международный институт стандартизации) – международный стандарт кодирования символов русского языка. На практике эта кодировка используется редко.

Ограниченный набор кодов (256) создает трудности для разработчиков единой системы кодирования текстовой информации. Вследствие этого было предложено кодировать символы не 8-разрядными двоичными числами, а числами с большим разрядом, что вызвало расширение диапазона возможных значений кодов. Система 16-разрядного кодирования символов называется универсальной – UNICODE. Шестнадцать разрядов позволяет обеспечить уникальные коды для 65 536 символов, что вполне достаточно для размещения в одной таблице символов большинства языков.

Несмотря на простоту предложенного подхода, практический переход на данную систему кодировки очень долго не мог осуществиться из-за недостатков ресурсов средств вычислительной техники, так как в системе кодирования UNICODE все текстовые документы становятся автоматически вдвое больше. В конце 1990-х гг. технические средства достигли необходимого уровня, начался постепенный перевод документов и программных средств на систему кодирования UNICODE.

Существует несколько способов кодирования графической информации.

При рассмотрении черно-белого графического изображения с помощью увеличительного стекла заметно, что в его состав входит несколько мельчайших точек, образующих характерный узор (или растр). Линейные координаты и индивидуальные свойства каждой из точек изображения можно выразить с помощью целых чисел, поэтому способ растрового кодирования базируется на использовании двоичного кода представления графических данных. Общеизвестным стандартом считается приведение черно-белых иллюстраций в форме комбинации точек с 256 градациями серого цвета, т. е. для кодирования яркости любой точки необходимы 8-разрядные двоичные числа.

В основу кодирования цветных графических изображений положен принцип разложения произвольного цвета на основные составляющие, в качестве которых применяются три основных цвета: красный (Red), зеленый (Green) и синий (Blue). На практике принимается, что любой цвет, который воспринимает человеческий глаз, можно получить с помощью механической комбинации этих трех цветов. Такая система кодирования называется RGB (по первым буквам основных цветов). При применении 24 двоичных разрядов для кодирования цветной графики такой режим носит название полноцветного (True Color).

Каждый из основных цветов сопоставляется с цветом, дополняющим основной цвет до белого. Для любого из основных цветов дополнительным будет являться цвет, который образован суммой пары остальных основных цветов. Соответственно среди дополнительных цветов можно выделить голубой (Cyan), пурпурный (Magenta) и желтый (Yellow). Принцип разложения произвольного цвета на составляющие компоненты используется не только для основных цветов, но и для дополнительных, т. е. любой цвет можно представить в виде суммы голубой, пурпурной и желтой составляющей. Этот метод кодирования цвета применяется в полиграфии, но там используется еще и четвертая краска – черная (Black), поэтому эта система кодирования обозначается четырьмя буквами – CMYK. Для представления цветной графики в этой системе применяется 32 двоичных разряда. Данный режим также носит название полноцветного.

При уменьшении количества двоичных разрядов, применяемых для кодирования цвета каждой точки, сокращается объем данных, но заметно уменьшается диапазон кодируемых цветов. Кодирование цветной графики 16-разрядными двоичными числами носит название режима High Color. При кодировании графической цветной информации с применением 8 бит данных можно передать только 256 оттенков. Данный метод кодирования цвета называется индексным.

В настоящий момент не существует единой стандартной системы кодирования звуковой информации, так как приемы и методы работы со звуковой информацией начали развиваться по сравнению с методами работы с другими видами информации самыми последними. Поэтому множество различных компаний, которые работают в области кодирования информации, создали свои собственные корпоративные стандарты для звуковой информации. Но среди этих корпоративных стандартов выделяются два основных направления.

В основе метода FM (Frequency Modulation) положено утверждение о том, что теоретически любой сложный звук может быть представлен в виде разложения на последовательность простейших гармонических сигналов разных частот. Каждый из этих гармонических сигналов представляет собой правильную синусоиду и поэтому может быть описан числовыми параметрами или закодирован. Звуковые сигналы образуют непрерывный спектр, т. е. являются аналоговыми, поэтому их разложение в гармонические ряды и представление в виде дискретных цифровых сигналов выполняется с помощью специальных устройств – аналого-цифровых преобразователей (АЦП). Обратное преобразование, которое необходимо для воспроизведения звука, закодированного числовым кодом, производится с помощью цифроаналоговых преобразователей (ЦАП). Из-за таких преобразований звуковых сигналов возникают потери информации, которые связаны с методом кодирования, поэтому качество звукозаписи с помощью метода FM обычно получается недостаточно удовлетворительным и соответствует качеству звучания простейших электромузыкальных инструментов с окраской, характерной для электронной музыки. При этом данный метод обеспечивает вполне компактный код, поэтому он широко использовался в те годы, когда ресурсы средств вычислительной техники были явно недостаточны.

Основная идея метода таблично-волнового синтеза (Wave-Table) состоит в том, что в заранее подготовленных таблицах находятся образцы звуков для множества различных музыкальных инструментов. Данные звуковые образцы носят название сэмплов. Числовые коды, которые заложены в сэмпле, выражают такие его характеристики, как тип инструмента, номер его модели, высоту тона, продолжительность и интенсивность звука, динамику его изменения, некоторые компоненты среды, в которой наблюдается звучание, и другие параметры, характеризующие особенности звучания. Поскольку для образцов применяются реальные звуки, то качество закодированной звуковой информации получается очень высоким и приближается к звучанию реальных музыкальных инструментов, что в большей степени соответствует нынешнему уровню развития современной компьютерной техники.

В зависимости от целей кодирования, различают следующие его виды:

- кодирование по образцу - используется всякий раз при вводе информации в компьютер для её внутреннего представления;

- криптографическое кодирование, или шифрование, – используется, когда нужно защитить информацию от несанкционированного доступа;

- эффективное, или оптимальное, кодирование – используется для устранения избыточности информации, т.е. снижения ее объема, например, в архиваторах;

- помехозащитное, или помехоустойчивое, кодирование – используется для обеспечения заданной

достоверности в случае, когда на сигнал накладывается помеха, например, при передаче информации по каналам связи.

Обнаружение ошибок - действие, направленное на контроль целостности данных при записи/воспроизведении информации. Исправление ошибок - процедура восстановления информации после чтения её из устройства хранения. Для обнаружения ошибок используют коды обнаружения ошибок, для исправления - корректирующие коды. В процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности данных и исправление ошибок - важные задачи на многих уровнях работы с информацией.

Существует несколько стратегий борьбы с ошибками: 1) обнаружение ошибок в блоках данных и автоматический запрос повторной передачи повреждённых блоков - этот подход применяется в основном на канальном и транспортном уровнях; 2) обнаружение ошибок в блоках данных и отбрасывание повреждённых блоков - такой подход иногда применяется в системах потокового мультимедиа, где важна задержка передачи и нет времени на повторную передачу; 3) исправление ошибок применяется на физическом уровне.

Корректирующие коды - коды, служащие для обнаружения или исправления ошибок, возникающих при передаче информации под влиянием помех, а также при её хранении.

Для этого при записи (передаче) в полезные данные добавляют специальным образом структурированную избыточную информацию (контрольное число), а при чтении (приёме) её используют для обнаружения или исправления ошибки. Число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода. С кодами, исправляющими ошибки, тесно связаны коды обнаружения ошибок. По способу работы с данными коды, исправляющие ошибки делятся на блоковые, делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и свёрточные, работающие с данными как с непрерывным потоком.

Хороший код должен удовлетворять, как минимум, следующим критериям: 1) способность исправлять как можно большее число ошибок, 2) как можно меньшая избыточность, 3) простота кодирования и декодирования.

Практически все используемые коды являются линейными. Это связано с тем, что нелинейные коды значительно сложнее исследовать, и для них трудно обеспечить приемлемую лёгкость кодирования и декодирования.

Линейный блоковый код - такой код, что множество его кодовых слов образует k-мерное линейное подпространство в n-мерном линейном пространстве, изоморфное пространству k-битных векторов. Это значит, что операция кодирования соответствует умножению исходного k-битного вектора на невырожденную матрицу, называемую порождающей матрицей.

Коды Хемминга - простейшие линейные коды с минимальным расстоянием 3, то есть способные исправить одну ошибку.

При передаче информации по каналу связи вероятность ошибки зависит от отношения сигнал/шум на входе демодулятора, поэтому при постоянном уровне шума решающее значение имеет мощность передатчика. В системах спутниковой или мобильной связи остро стоит вопрос экономии энергии, а в телефонной связи неограниченно повышать мощность сигнала не дают технические ограничения.

Поскольку помехоустойчивое кодирование позволяет исправлять ошибки, при его применении мощность передатчика можно снизить, оставляя скорость передачи информации неизменной. Энергетический выигрыш определяется как разница отношений сигнал/шум при наличии и отсутствии кодирования. Коды, исправляющие ошибки, применяются: 1) в системах цифровой связи, в том числе: спутниковой, радиорелейной, сотовой, передаче данных по телефонным каналам. 2) в системах хранения информации, в том числе магнитных и оптических. Коды, обнаруживающие ошибки, используются в сетевых протоколах различных уровней.

Первая теорема Шеннона о передаче информации, которая называется также основной теоремой о кодировании при отсутствии помех, формулируется следующим образом:

При отсутствии помех передачи всегда возможен такой вариант кодирования сообщения, при котором среднее число знаков кода, приходящихся на один знак кодируемого алфавита, будет сколь угодно близко к отношению средних информаций на знак первичного и вторичного алфавитов. Используя понятие избыточности кода, можно дать более короткую формулировку теоремы:

При отсутствии помех передачи всегда возможен такой вариант кодирования сообщения, при котором избыточность кода будет сколь угодно близкой к нулю.

Определение количества переданной информации при двоичном кодировании сводится к простому подсчету числа импульсов (единиц) и пауз (нулей). При этом возникает проблема выделения из потока сигналов (последовательности импульсов и пауз) отдельных кодов. Приемное устройство фиксирует интенсивность и длительность сигналов. Элементарные сигналы (0 и 1) могут иметь одинаковые или разные длительности. Их количество в коде (длина кодовой цепочки), который ставится в соответствие знаку первичного алфавита, также может быть одинаковым (в этом случае код называется равномерным) или разным (неравномерный код). Наконец, коды могут строиться для каждого знака исходного алфавита (алфавитное кодирование) или для их комбинаций (кодирование блоков, слов).

В случае использования неравномерного кодирования или сигналов разной длительности для отделения кода одного знака от другого между ними необходимо передавать специальный сигнал – временной разделитель (признак конца знака) или применять такие коды, которые оказываются уникальными, т.е. несовпадающими с частями других кодов. При равномерном кодировании одинаковыми по длительности сигналами передачи специального разделителя не требуется, поскольку отделение одного кода от другого производится по общей длительности, которая для всех кодов оказывается одинаковой (или одинаковому числу бит при хранении).

Можно построить такую систему кодирования, чтобы суммарная длительность кодов при передаче (или суммарное число кодов при хранении) данного сообщения была бы наименьшей.

Существуют два классических метода эффективного кодирования: метод Шеннона-Фано и метод Хаффмена. Входными данными для обоих методов является заданное множество исходных символов для кодирования с их частотами; результат - эффективные коды.

Метод Шеннона-Фано. Этот метод требует упорядочения исходного множества символов по не возрастанию их частот. Затем выполняются следующие шаги:

а) список символов делится на две части (назовем их первой и второй частями) так, чтобы суммы частот обеих частей (назовем их Σ1 и Σ2) были точно или примерно равны. В случае, когда точного равенства достичь не удается, разница между суммами должна быть минимальна;

б) кодовым комбинациям первой части дописывается 1, кодовым комбинациям второй части дописывается 0;

в) анализируют первую часть: если она содержит только один символ, работа с ней заканчивается, – считается, что код для ее символов построен, и выполняется переход к шагу г) для построения кода второй части. Если символов больше одного, переходят к шагу а) и процедура повторяется с первой частью как с самостоятельным упорядоченным списком;

г) анализируют вторую часть: если она содержит только один символ, работа с ней заканчивается и выполняется обращение к оставшемуся списку (шаг д). Если символов больше одного, переходят к шагу а) и процедура повторяется со второй частью как с самостоятельным списком;

д) анализируется оставшийся список: если он пуст – код построен, работа заканчивается. Если нет, – выполняется шаг а).

Метод Хаффмена. Этот метод имеет два преимущества по сравнению с методом Шеннона-Фано: он устраняет неоднозначность кодирования, возникающую из-за примерного равенства сумм частот при разделении списка на две части (линия деления проводится неоднозначно), и имеет, в общем случае, большую эффективность кода. Исходное множество символов упорядочивается по не возрастанию частотыи выполняются следующие шаги:

1) объединение частот: две последние частоты списка складываются, а соответствующие символы исключаются из списка; оставшийся после исключения символов список пополняется суммой частот и вновь упорядочивается; предыдущие шаги повторяются до тех пор, пока ни получится единица в результате суммирования и список ни уменьшится до одного символа;

2) построение кодового дерева: строится двоичное кодовое дерево: корнем его является вершина, полученная в результате объединения частот, равная 1; листьями – исходные вершины; остальные вершины соответствуют либо суммарным, либо исходным частотам, причем для каждой вершины левая подчиненная вершина соответствует большему слагаемому, а правая – меньшему; ребра дерева связывают вершины- суммы с вершинами-слагаемыми. Структура дерева показывает, как происходило объединение частот; ребра дерева кодируются: каждое левое кодируется единицей, каждое правое – нулём;

3) формирование кода: для получения кодов листьев (исходных кодируемых символов) продвигаются от корня к нужной вершине и «собирают» веса проходимых рёбер.

Таким образом, можно заключить, что существует метод построения оптимального неравномерного алфавитного кода. Не следует думать, что он представляет число теоретический интерес. Метод Хаффмана и его модификация – метод адаптивного кодирования (динамическое кодирование Хаффмана) – нашли широчайшее применение в программах-архиваторах, программах резервного копирования файлов и дисков, в системах сжатия информации в модемах и факсах.

10. Аналого-цифровые преобразователи сигналов (АЦП) (использование АЦП для преобразования сигналов от датчиков параметров технологических процессов, структурная схема АЦП конвейерного типа). Цифро-аналоговый преобразователь (ЦАП) (принцип работы и структурная схема ЦАП, сглаживание сигналов на выходе ЦАП).

Аналого-цифровой преобразователь^[1][2][3] (АЦП, англ. Analog-to-digital converter, ADC) — устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал). Обратное преобразование осуществляется при помощи ЦАП (цифро-аналогового преобразователя, DAC).

Как правило, АЦП — электронное устройство, преобразующее напряжение в двоичный цифровой код. Тем не менее, некоторые неэлектронные устройства с цифровым выходом, следует также относить к АЦП, например, некоторые типыпреобразователей угол-код. Простейшим одноразрядным двоичным АЦП является компаратор.

По способу применяемых алгоритмов АЦП делят на:

• Последовательные прямого перебора

• Последовательного приближения

• Последовательные с сигма-дельта-модуляцией

• Параллельные одноступенчатые

• Параллельные двух- и более ступенчатые (конвейерные)

Передаточная характеристика АЦП — зависимость числового эквивалента выходного двоичного кода от величины входного аналогового сигнала. Говорят о линейных и нелинейных АЦП. Такое деление условное. Обе передаточные характеристики — ступенчатые. Но для «линейных» АЦП всегда возможно провести такую прямую линию, чтобы все точки передаточной характеристики, соответствующие входным значениям delta*2^k (где delta — шаг дискретизации, k лежит в диапазоне 0..N, где N — разрядность АЦП) были от неё равноудалены.

Для преобразования любого аналогового сигнала (звука, изображения) в цифровую форму необходимо выполнить три основные операции: дискретизацию, квантование и кодирование.

Дискретизация - представление непрерывного аналогового сигнала последовательностью его значений (отсчетов ). Эти отсчеты берутся в моменты времени, отделенные друг от друга интервалом, который называется интервалом дискретизации. Величину, обратную интервалу между отсчетами, называют частотой дискретизации.

Понятно, что чем меньше интервал дискретизации и, соответственно, выше частота дискретизации, тем меньше различия между исходным сигналом и его дискретизированной копией. Ступенчатая структура дискретизированного сигнала может быть сглажена с помощью фильтра нижних частот. Таким образом и осуществляется восстановление аналогового сигнала из дискретизированного. Но восстановление будет точным только в том случае, если частота дискретизации по крайней мере в 2 раза превышает ширину полосы частот исходного аналогового сигнала (это условие определяется известной теоремой Котельникова). Если это условие не выполняется, то дискретизация сопровождается необратимыми искажениями. Дело в том, что в результате дискретизации в частотном спектре сигнала появляютсся дополнительные компоненты, располагающиеся вокруг гармоник частоты дискретизации в диапазоне, равном удвоенной ширине спектра исходного аналогового сигнала. Если максимальная частота в частотном спектре аналогового сигнала превышает половину частоты дискретизации, то дополнительные компоненты попадают в полосу частот исходного аналогового сигнала. В этом случае уже нельзя восстановить исходный сигнал без искажений.

Квантование представляет собой замену величины отсчета сигнала ближайшим значением из набора фиксированных величин - уровней квантования. Другими словами, квантование - это округление величины отсчета. Уровни квантования делят весь диапазон возможного изменения значений сигнала на конечное число интервалов - шагов квантования. Расположение уровней квантования обусловлено шкалой квантования. Используются как равномерные, так и неравномерные шкалы. Искажения сигнала, возникающие в процессе квантования, называют шумом квантования. При инструментальной оценке шума вычисляют разность между исходным сигналом и его квантованной копией, а в качестве объективных показателей шума принимают, например, среднеквадратичное значение этой разности. В отличие от флуктуационных шумов шум квантования коррелирован с сигналом, поэтому шум квантования не может быть устранен последующей фильтрацией. Шум квантования убывает с увеличением числа уровней квантования.

Цифровое кодирование.

Квантованный сигнал, в отличие от исходного аналогового, может принимать только конечное число значений. Это позволяет представить его в пределах каждого интервала дискретизации числом, равным порядковому номеру уровня квантования. В свою очередь это число можно выразить комбинацией некоторых знаков или символов. Совокупность знаков (символов) и система правил, при помощи которых данные представляются в виде набора символов, называют кодом. Конечная последовательность кодовых символов называется кодовым словом. Квантованный сигнал можно преобразовать в последовательность кодовых слов. Эта операция и называется кодированием. Каждое кодовое слово передается в пределах одного интервала дискретизации. Для кодирования сигналов звука и изображения широко применяют двоичный код. Если квантованный сигнал может принимать N значений, то число двоичных символов в каждом кодовом слове n >= log2N. Один разряд, или символ слова, представленного в двоичном коде, называют битом. Обычно число уровней квантования равно целой степени числа 2, т.е. N = 2n.

Кодовые слова можно передавать в параллельной или последовательной формах. Для передачи в параллельной форме надо использовать n линий связи. Символы кодового слова одновременно передаются по линиям в пределах интервала дискретизации. Для передачи в последовательной форме интервал дискретизации надо разделить на n подинтервалов - тактов. В этом случае символы слова передаются последовательно по одной линии, причем на передачу одного символа слова отводится один такт. Каждый символ слова передается с помощью одного или нескольких дискретных сигналов - импульсов. Преобразование аналогового сигнала в последовательность кодовых слов поэтому часто называют импульсно-кодовой модуляцией. Форма представления слов определенными сигналами определяется форматом кода. Можно, например, устанавливать в пределах такта высокий уровень сигнала, если в данном такте передается двоичный символ 1, и низкий - если передается двоичный символ 0 (такой способ представления, показанный на рис. 6, называют форматом БВН - Без Возвращения к Нулю). В параллельном цифровом потоке по каждой линии в пределах интервала дискретизации передается 1 бит 4-разрядного слова. В последовательном потоке интервал дискретизации делится на 4 такта, в которых передаются (начиная со старшего) биты 4-разрядного слова.

Система сбора данных (ССД) - это набор аппаратных средств, осуществляющий выборку, преобразование, хранение и первоначальную обработку различных входных аналоговых сигналов. Система сбора данных является основным элементом многоканальных средств измерений, определяющим его технические характеристики.

В состав ССД могут входить фильтры нижних частот (ФНЧ), нормирующие усилители (НУ), аналоговый мультиплексор (MUX), устройство выборки и хранения (УВХ), аналого-цифровой преобразователь (АЦП) и микроконтроллер (МК). Некоторые типы ССД содержат программируемый усилитель после мультиплексора, что позволяет перестраивать диапазон измерений.

На вход ССД поступают аналоговые сигналы, например - с датчиков физических величин. Тип и уровень аналогового сигнала определяется физическими особенностями применяемых датчиков. Как правило, сигнал мал по амплитуде, и в нем присутствуют нежелательные шумы и помехи. Фильтр нижних частот производит фильтрацию и предотвращает наложение спектров сигнала. Нормирующий усилитель согласует по амплитуде сигнал первичного преобразователя с входным диапазоном АЦП. Аналоговый мультиплексор обеспечивает коммутацию выбранного аналогового входного канала с УВХ. Устройство выборки-хранения производит хранение сигнала в течение всего периода времени преобразования аналого-цифрового преобразователя. АЦП осуществляет преобразование напряжения с входного аналогового канала в цифровой код. Далее цифровой код, пропорциональный входному сигналу с датчика, поступает в микроконтроллер, где происходит его первоначальная обработка.

ССД используются в различных областях, таких как прецизионные низкочастотные измерения, акустика, а также в высокоскоростных измерениях. Несмотря на близкую структуру, в зависимости от области применения к ССД, к ним могут предъявляться различные требования. В некоторых случаях используются и другие структуры ССД, Например, структура с несколькими УВХ (рисунок 2а). Эта структура используется, когда необходимо произвести выборку значений двух или большего числа сигналов точно в один и тот же момент времени (одновременная выборка).

Состояние машин и установок можно контролировать не только человеком, но и специальными устройствами, называемыми чувствительными элементами или датчиками. Датчики применяются как в автоматике, так и в измерительной технике и являются устройствами автоматики и измерений.

Работа систем автоматики основана на информации описывающей состояние ее выходов и отдельных устройств, которая передается в виде электрических, пневматических, гидравлических и т.д. сигналов. Одним из способов получения такой информации является измерение выходов управляемого объекта - всевозможных (механических, тепловых, оптических, электромагнитных и т.п.) физических величин. В современных системах автоматики наибольшее количество информации преобразуется, обрабатывается и передается в виде электрических или оптических сигналов.

Устройство, которое преобразует какую-либо физическую величину (давление, скорость, тепло ...) в другую (сигнал), которую удобнее усиливать, измерять, передавать и обрабатывать называется датчиком. В основном датчик воздействует на электрическую цепь, включая или выключая ее, изменяя электрическое сопротивление или вырабатывая электричество.

Преобразование сигналов в датчиках происходит в два этапа:

• Преобразование вида сигнала, например механический в электрический;

• Придание преобразованному сигналу стандартного вида, приемлемого для систем автоматики - нормирование.

Первичный преобразователь в датчике является чувствительным элементом к измеряемой физической величине и преобразует ее в электрическую, которая измеряется при помощи стандартных схем.

Вторичное преобразование осуществляется: усилителями, аналого-цифровыми преобразователями (АЦП), цифро-аналоговыми преобразователями (ЦАП), импульсными и кодовыми преобразователями и т.п. Фактически датчик представляет совокупность трех элементов:

• первичного преобразователя;

• измерительной схемы;

• вторичного, нормирующего преобразователя для придачи сигналу на выходе датчика стандартного вида.

В зависимости от объема собираемой информации датчики разделяются следующим образом:

• определяющие наличие или отсутствие сигнала - однобитовые;

• определяющие соответствует ли сигнал желаемому, а также знак отклонения - двубитовые;

Конвеерные АЦП.

Быстродействие многоступенчатого АЦП можно повысить, применив конвеерный принцип многоступенчатой обработки входного сигнала. В обыкновенном многоступенчатом АЦП (рис. 4) вначале происходит формирование старших разрядов выходного слова преобразователем АЦП1, а затем идет период установления выходного сигнала ЦАП.

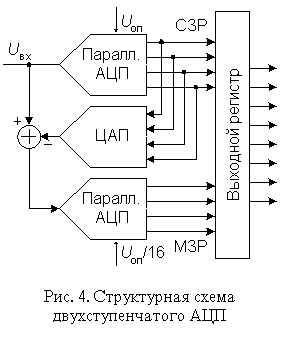
На этом интервале АЦП2 простаивает. На втором этапе во время преобразования остатка преобразователем АЦП2 простаивает АЦП1. Введя элементы задержки аналогового и цифрового сигналов между ступенями преобразователя, получим конвеерный АЦП, схема 8-разрядного варианта которого приведена на рис. 6.

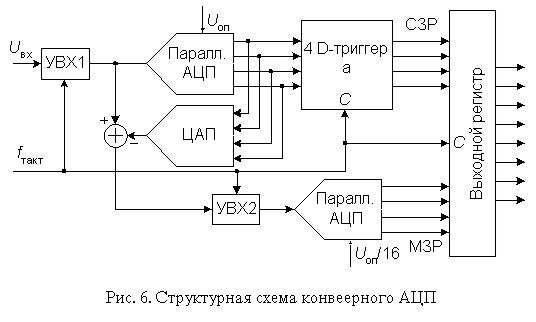
Роль аналогового элемента задержки выполняет устройство выборки-хранения УВХ2, а цифрового - четыре D-триггера. Триггеры задерживают передачу старшего полубайта в выходной регистр на один период тактового сигнала CLK.

Сигналы выборки, формируемые из тактового сигнала, поступают на УВХ1 и УВХ2 в разные моменты времени. УВХ2 переводится в режим хранения позже, чем УВХ1 на время, равное суммарной задержке распространения сигнала по АЦП1 и ЦАП. Задний фронт тактового сигнала управляет записью кодов в D-триггеры и выходной регистр. Полная обработка входного сигнала занимает около двух периодов CLK, но частота появления новых значений выходного кода равна частоте тактового сигнала.

Таким образом, конвеерная архитектура позволяет существенно (в несколько раз) повысить максимальную частоту выборок многоступенчатого АЦП. То, что при этом сохраняется суммарная задержка прохождения сигнала, соответствующая обычному многоступенчатому АЦП с равным числом ступеней, не имеет существенного значения, так как время последующей цифровой обработки этих сигналов все равно многократно превосходит эту задержку. За счет этого можно без проигрыша в быстродействии увеличить число ступеней АЦП, понизив разрядность каждой ступени. В свою очередь, увеличение числа ступеней преобразования уменьшает сложность АЦП. Действительно, например, для построения 12-разрядного АЦП из четырех 3-разрядных необходимо 28 компараторов, тогда как его реализация из двух 6-разрядных потребует 126 компараторов.

Конвеерную архитектуру имеет большое количество выпускаемых в настоящее время многоступенчатых АЦП. В частности, 2-ступенчатый 10-разрядный AD9040А, выполняющий до 40 млн. преобразований в секунду (МПс), 4-ступенчатый 12-разрядный AD9220 (10 МПс), потребляющий всего 250 мВт, и др. При выборе конвеерного АЦП следует иметь в виду, что многие из них не допускают работу с низкой частотой выборок. Например, изготовитель не рекомендует работу ИМС AD9040А с частотой преобразований менее 10 МПс, 3-ступенчатого 12-разрядного AD9022 с частотой менее 2 МПс и т.д. Это вызвано тем, что внутренние УВХ имеют довольно высокую скорость разряда конденсаторов хранения, поэтому работа с большим тактовым периодом приводит к значительному изменению преобразуемого сигнала в ходе преобразования.

Цифро-аналоговый преобразователь (ЦАП) — устройство для преобразования цифрового (обычно двоичного) кода в аналоговый сигнал (ток, напряжение или заряд). Цифро-аналоговые преобразователи являются интерфейсом между дискретным цифровым миром и аналоговыми сигналами.

Аналого-цифровой преобразователь (АЦП) производит обратную операцию.

Звуковой ЦАП обычно получает на вход цифровой сигнал в импульсно-кодовой модуляции (англ. PCM, pulse-code modulation). Задача преобразования различных сжатых форматов в PCM выполняется соответствующими кодеками.

Наиболее общие типы электронных ЦАП:

• Широтно-импульсный модулятор — простейший тип ЦАП. Стабильный источник тока или напряжения периодически включается на время, пропорциональное преобразуемому цифровому коду, далее полученная импульсная последовательность фильтруется аналоговым фильтром нижних частот. Такой способ часто используется для управления скоростью электромоторов, а также становится популярным в Hi-Fi-аудиотехнике;

• ЦАП передискретизации, такие как дельта-сигма-ЦАП, основаны на изменяемой плотности импульсов. Передискретизация позволяет использовать ЦАП с меньшей разрядностью для достижения большей разрядности итогового преобразования; часто дельта-сигма ЦАП строится на основе простейшего однобитного ЦАП, который является практически линейным. На ЦАП малой разрядности поступает импульсный сигнал с модулированной плотностью импульсов (c постоянной длительностью импульса, но с изменяемой скважностью), создаваемый с использованием отрицательной обратной связи. Отрицательная обратная связь выступает в роли фильтра верхних частот для шума квантования.

Большинство ЦАП большой разрядности (более 16 бит) построены на этом принципе вследствие его высокой линейности и низкой стоимости. Быстродействие дельта-сигма ЦАП достигает сотни тысяч отсчетов в секунду, разрядность — до 24 бит. Для генерации сигнала с модулированной плотностью импульсов может быть использован простой дельта-сигма модулятор первого порядка или более высокого порядка как MASH (англ. Multi stage noise SHaping). С увеличением частоты передискретизации смягчаются требования, предъявляемые к выходному фильтру низких частот и улучшается подавление шума квантования;

• ЦАП взвешивающего типа, в котором каждому биту преобразуемого двоичного кода соответствует резистор или источник тока, подключенный на общую точку суммирования. Сила тока источника (проводимость резистора) пропорциональна весу бита, которому он соответствует. Таким образом, все ненулевые биты кода суммируются с весом. Взвешивающий метод один из самых быстрых, но ему свойственна низкая точность из-за необходимости наличия набора множества различных прецизионных источников или резисторов и непостоянного импеданса. По этой причине взвешивающие ЦАП имеют разрядность не более восьми бит;

• ЦАП лестничного типа (цепная R-2R-схема). В R-2R-ЦАП значения создаются в специальной схеме, состоящей из резисторов с сопротивлениями R и 2R, называемой матрицей постоянного импеданса, которая имеет два вида включения: прямое — матрица токов и инверсное — матрица напряжений. Применение одинаковых резисторов позволяет существенно улучшить точность по сравнению с обычным взвешивающим ЦАП, так как сравнительно просто изготовить набор прецизионных элементов с одинаковыми параметрами. ЦАП типа R-2R позволяют отодвинуть ограничения по разрядности. С лазерной подгонкой резисторов на одной подложке достигается точность 20-22 бита. Основное время на преобразование тратится в операционном усилителе, поэтому он должен иметь максимальное быстродействие. Быстродействие ЦАП единицы микросекунд и ниже (то есть наносекунды);

ЦАП широко применяется в различных устройствах автоматики для связи цифровых ЭВМ с аналоговыми элементами и системами.

Принцип работы ЦАП состоит в суммировании аналоговых сигналов, пропорциональных весам разрядов входного цифрового кода, с коэффициентами, равными нулю или единице в зависимости от значения соответствующего разряда кода.

ЦАП преобразует цифровой двоичный код Q₄Q₃Q₂Q₁ в аналоговую величину, обычно напряжение U_вых.. Каждый разряд двоичного кода имеет определенный вес i-го разряда вдвое больше, чем вес (i-1)-го. Работу ЦАП можно описать следующей формулой:

U_вых=e*(Q₁ 1+Q₂*2+Q₃*4+Q₄*8+…), (1)

где e - напряжение, соответствующее весу младшего разряда, Q_i - значение i -го разряда двоичного кода (0 или 1).

Например, числу 1001 соответствует

U_вых=у*(1*1+0*2+0*4+1*8)=9*e, а числу 1100

U_вых=e*(0*1+0*2+1*4+1*8)=12*e.

На рисунке 3.3.4.1 приведена схема цифро - аналогового преобразователя.

Рисунок 3.3.4.1 - Схема цифро-аналогового преобразователя

 В схеме i – й ключ замкнут при Q_i=1, при Q_i=0 – разомкнут. Регистры подобраны таким образом, что R>>Rн.

Эквивалентное сопротивление обведенного пунктиром двухполюсника Rэк и сопротивление нагрузки Rн образуют делитель напряжения, тогда

Uвых = E Rн / Rэк + Rн » E*Rн / Rэк  (2)

Проводимость двухполюсника 1 / Rэк равна сумме проводимостей ветвей (при Q_i=1 i – ветвь включена, при Q_i=0 – отключена):

1 / Rэк = Q1 / 8R + Q2 / 4R + Q3 / 2R + Q4 / R   (3)

Подставив (3) в (2), получаем выражение, идентичное (1)

Uвых = (8Е Rн / R)*( Q₁*1 + Q₂*2 + Q₃*4 + Q₄*8 )

Очевидно, что е = 8Е Rн / R. Выбором е можно установить требуемый масштаб аналоговой величины.

На выходе ЦАП формируется точно такой же ступенчатый аналоговый сигнал, который получался при дискретизации и удерживании. Подобный ступенчатый, или «лестничный» эффект представляет собой искажение, которое необходимо устранить до того, как аналоговый сигнал будет использоваться. Для устранения этого эффекта применяют низкочастотные сглаживающие фильтры, которые иногда путают с «анти-элайсинговыми» фильтрами.