1.2.2. Принцип компенсации

 

Е сли возмущающий фактор искажает выходную величину до недопустимых пределов, то применяютпринцип компенсации (рис.6, КУ - корректирующее устройство).

Пусть y_о - значение выходной величины, которое требуется обеспечить согласно программе. На самом деле из-за возмущения f на выходе регистрируется значение y. Величина e = y_о - yназывается отклонением от заданной величины. Если каким-то образом удается измерить величинуf, то можно откорректировать управляющее воздействие u на входе ОУ, суммируя сигнал УУ с корректирующим воздействием, пропорциональным возмущению f и компенсирующим его влияние.

Примеры систем компенсации: биметаллический маятник в часах, компенсационная обмотка машины постоянного тока и т.п. На рис.6 в цепи НЭ стоит термосопротивление R_t, величина которого меняется в зависимости от колебаний температуры окружающей среды, корректируя напряжение на НЭ.

Достоинство принципа компенсации: быстрота реакции на возмущения. Он более точен, чем принцип разомкнутого управления. Недостаток: невозможность учета подобным образом всех возможных возмущений.

 

1.2.3. Принцип обратной связи

 

Н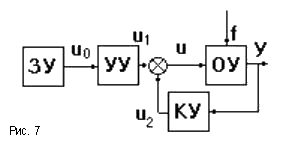 аибольшее распространение в технике получил принцип обратной связи (рис.7). Здесь управляющее воздействие корректируется в зависимости от выходной величины y(t). И уже не важно, какие возмущения действуют на ОУ. Если значение y(t) отклоняется от требуемого, то происходит корректировка сигнала u(t) с целью уменьшения данного отклонения. Связь выхода ОУ с его входом называется главной обратной связью (ОС).

В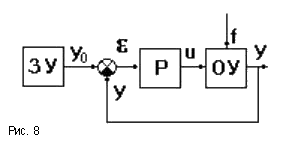 частном случае (рис.8) ЗУ формирует требуемое значение выходной величины y_о(t), которое сравнивается с действительным значением на выходе САУ y(t). Отклонение e = y_о-y с выхода сравнивающего устройства подается на вход регулятора Р, объединяющего в себе УУ, УО, ЧЭ. Если e 0, то регулятор формирует управляющее воздействие u(t), действующее до тех пор, пока не обеспечится равенство e = 0, или y = y_о. Так как на регулятор подается разность сигналов, то такая обратная связь называется отрицательной, в отличие от положительной обратной связи, когда сигналы складываются.

Такое управление в функции отклонения называется регулированием, а подобную САУ называютсистемой автоматического регулирования (САР). Так на рис.9 изображена упрощенная схема САР хлебопекарной печи. Р оль ЗУ здесь выполняет потенциометр, напряжение на котором U_з сравнивается с напряжением на термопареU_т. Их разность  U через усилитель подается на исполнительный двигатель ИД, регулирующий через редуктор положение движка реостата в цепи НЭ. Наличие усилителя говорит о том, что данная САР является системой непрямого регулирования, так как энергия для функций управления берется от посторонних источников питания, в отличие от систем прямого регулирования, в которых энергия берется непосредственно от ОУ, как, например, в САР уровня воды в баке (рис.10).

Недостатком принципа обратной связи является инерционность системы. Поэтому часто применяют комбинацию данного принципа с принципом компенсации, что позволяет объединить достоинства обоих принципов: быстроту реакции на возмущение принципа компенсации и точность регулирования независимо от природы возмущений принципа обратной связи.

Линейная система — математическая модель системы, оператор которой обладает свойством линейности.

Необходимые условия линейности системы:

• 1. Гомогенность – при изменении амплитуды входного сигнала в k раз также в k раз изменяется и амплитуда выходного сигнала.

• 2. Аддитивность – при суммировании входных сигналов результирующий сигнал на выходе будет равен сумме реакций от исходных сигналов.

• 3. Инвариантность – когда смещение входного сигнала во времени вызывает аналогичное смещение выходного сигнала.

• 4. Статическая линейность – когда основные законы в системе описываются линейными уравнениями.

• 5. Гармоническая верность – если на вход системы подать синусоидальный сигнал, то на выходе будет сигнал той же частоты.

На основе изучения многих моделей систем, можно прийти к выводу, что системы, описываемые линейными дифференциальными уравнениями, несмотря на все их многообразие, обладают весьма ограниченным числом основных свойств. Эти свойства следующие:

• способность системы к усилению (ослаблению) сигнала;

• способность системы к накоплению (энергии, материи);

• инерционность;

• прогнозируемость;

• колебательность;

• устойчивость;

• запаздывание.

Свойства линейных систем:

1. Порядок установки линейных систем не влияет на результирующий сигнал.

2. Любая сложная система будет линейна, если составлена из линейных систем и блоков суммирования.

3. Перемножение сигнала на константу является линейной операцией, а перемножение двух сигналов – нелинейной.

Система линейных уравнений объекта. В общем случае модель одноканального объекта управления описывается нелинейным дифференциальным уравнением (системой уравнений), связывающим входной сигнал управления u(t) и выходной сигнал состояния объекта y(t):

F(y', y", …, y⁽ⁿ⁾, u', u", …, u^(m)) = 0. (3.2.1)

Уравнение описывает динамическое состояние ОУ на некотором временном интервале t≥t_o, и связывает входные сигналы u(t) и их производные u⁽ⁿ⁾(t) с выходными сигналами y(t) и их производными y⁽ⁿ⁾(t). Значения у(t_o) = у_о, у'(t_o) = у'_о, ... , y⁽ⁿ⁾(t_o) = у⁽ⁿ⁾_о называются начальными значениями (условиями), а число г = n-m ≥ 1- относительной степенью модели.

Классом дифференциальных уравнений, удобным для проведения исследований, являются линейные дифференциальные уравнения. Переход к линейным дифференциальным уравнениям выполняется операцией линеаризации, при которой переменные уравнения (3.2.1) заменяются новыми переменными – отклонениями от некоторого номинального режима (y=y-y_н, u= u-u_н), начало координат переносится в точку номинального режима, а функция F раскладывается в ряд Тейлора в окрестностях этой точки по частным производным. В результате линеаризации получаем следующую систему линейных уравнений в отклонениях:

A₀(t)y⁽ⁿ⁾ + A₁(t)y^(n-1) +…+ A_n(t)y = B₀(t)u^(m) + В₁(t)y^(m-1) +…+ B_m(t)u. (3.2.2)

Порядок системы уравнений равен n по порядку производной y⁽ⁿ⁾(t), n ≥ m, так как при n < m системы технически нереализуемы. Так как все частные производные представляют собой либо постоянные матрицы, либо матрицы, зависящие только от времени, то полученное уравнение есть либо система линейных дифференциальных уравнений с постоянными коэффициентами (A_j(t) = a_j = const, B_j(t) = b_j = const), либо система с переменными коэффициентами, в зависимости от номинальной траектории.

В случае постоянных коэффициентов система называется стационарной. Как правило, входные и выходные величины объекта - скалярные функции, при этом уравнение (3.2.2) принимает вид:

a₀y⁽ⁿ⁾ + a₁y^(n-1) +…+ a_ny = b₀u^(m) + b₁y^(m-1) +…+ b_mu. (3.2.3)

где a_j, b_j – постоянные коэффициенты (параметры) модели, a₀ > 0, b₀ > 0, n - порядок модели, 0 ≤ m < n. Решение уравнений таких стационарных объектов относительно y(t) является главным объектом исследований в классической теории автоматического управления.

Система, для которой u(t)≡ 0, называется автономной. Описание автономной системы дается однородным дифференциальным уравнением вида

a₀y⁽ⁿ⁾ + a₁y^(n-1) +…+ a_ny = 0. (3.2.3')

Разностные уравнения. Связь между значениями решетчатой функции при разных значениях аргумента определяется с помощью конечных разностей, которые являются аналогами производных в дифференциальных уравнениях.

Разностью первого порядка (первой разностью) называется разность между последующим дискретным значением решетчатой функции и ее текущим значением:

Dx(k) = x(k+1) – x(k).

Разность первого порядка характеризует скорость изменения решетчатой функции и, следовательно, является аналогом первой производной непрерывной функции.

Разность второго порядка определяется как разность двух соседних разностей первого порядка:

D²x(k) = Dx(k+1) - Dx(k) = [x(k+2)-x(k+1)] – [x(k+1)-x(k)] = x(k+2) - 2x(k+1) + x(k).

Разности любого m-го порядка вычисляются аналогично:

D^mx(k) = D^m-1x(k+1) - D^m-1x(k).

D^mx(k) = (-1)ⁿ x(k+m-n) m!/[k!(m-n)!].

Математические модели САУ

Для описания сигналов и систем, в зависимости от используемых методов исследования, применяются различные формы их представления во временной, частотной или операторной области. Взаимосвязь между областями осуществляется с помощью преобразований Фурье и Лапласа, как показано на рис. 3.

Рис. 3

Преобразование Фурье. Соответствие между временным и частотным представлением сигнала можно выразить через преобразование Фурье:

(2.1)

и обратное преобразование Фурье:

 (2.2)

 

Преобразование Лапласа. Соответствие между временным и операторным представлением сигнала можно выразить через преобразование Лапласа:

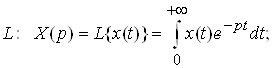(2.3)

и обратное преобразование Лапласа:

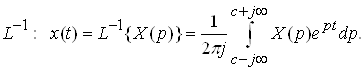 (2.4)

где р = c+ jw – оператор Лапласа, c – область сходимости, x(t) – оригинал, а X(p) – изображение.

Для дискретных систем используют дискретные преобразования Лапласа и Фурье, а также ряд других преобразований (Z, W и др.).

Дискретное z-преобразование. В теории импульсных систем для решения разностных уравнений используется дискретное преобразование Лапласа и его модификация - дискретное z-преобразование.

Преобразование Лапласа для непрерывной функции х(t):

X(р) = x(t) exp(-pt) dt. (6.2.3)

При переходе к дискретной функции x(kТ), заменяя интегрирование суммированием:

X(p) =T x(kT) exp(-pkT). (6.2.4)

Введем новую переменную z=exp(pt):

X(z) =T x(kT) z^-k . (6.2.5)

Это уравнение представляет собой дискретное преобразование Лапласа, в котором выражение

X(z) = x(kT) z^-k . (6.2.6)

называется z-преобразованием. Оно лежит в основе метода решения разностных уравнений. Дискретное преобразование Лапласа X(z) отличается от z-преобразования наличием нормирующего множителя Т. При анализе дискретных систем z-преобразование позволяет перейти от разностных уравнений к алгебраическим и существенно упростить анализ динамики дискретных систем.

В выражении (6.2.6) функция х(kТ) называется оригиналом решетчатой функции, a X(z) – ее изображением. Для обратного перехода от изображения к оригиналу (для нахождения исходной решетчатой функции по ее изображению) используется обратное z-преобразование:

x(kT) = (1/2pj) ∮ X(z) z^k-1 dz.

Корни p_i характеристического полинома непрерывной системы связаны с корнями z_i характеристического полинома эквивалентной дискретной системы соотношением

z_i = exp(Tp_i). (6.2.7)

В общем случае, отображение (6.2.7) неоднозначно, и нескольким различным значениям p_i может соответствовать одно и то же значение z_i.

Передаточная функция — один из способов математического описания динамической системы. Используется в основном в теории управления, связи, цифровой обработке сигналов. Представляет собой дифференциальный оператор, выражающий связь между входом и выходом линейной стационарной системы. Зная входной сигнал системы и передаточную функцию, можно восстановить выходной сигнал.

В теории управления передаточная функция непрерывной системы представляет собой отношение преобразования Лапласа выходного сигнала к преобразованию Лапласа входного сигнала при нулевых начальных условиях.

Линейные стационарные системы

Пусть   — входной сигнал линейной стационарной системы, а   — её выходной сигнал. Тогда передаточная функция   такой системы записывается в виде:

,

где   и   — преобразования Лапласа для сигналов   и   соответственно:

,

.

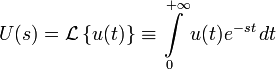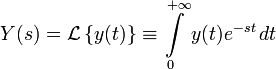Дискретная передаточная функция

Для дискретных и дискретно-непрерывных систем вводится понятие дискретной передаточной функции. Пусть   — входной дискретный сигнал такой системы, а   — её дискретный выходной сигнал,  . Тогда передаточная функция   такой системы записывается в виде:

,

где   и   — z-преобразования для сигналов   и   соответственно:

,

.

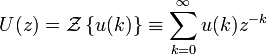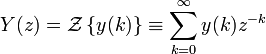Критерии устойчивости

Критерий Рауса

Для определения устойчивости системы строятся таблицы вида:

Коэффициенты	Строки	столбец 1	столбец 2	столбец 3
	1
	2
	3
	4

Для устойчивости системы необходимо, чтобы все элементы первого столбца имели положительные значения; если в первом столбце присутствуют отрицательные элементы — система неустойчива; если хотя бы один элемент равен нулю, а остальные положительны, то система на границе устойчивости.

Критерий Гурвица

  — Определитель Гурвица

Теорема: Для устойчивости замкнутой САУ необходимо и достаточно, чтобы определитель Гурвица и все его миноры были положительны при 

Критерий Михайлова

Заменим   , где ω — угловая частота колебаний, соответствующих чисто мнимому корню данного характеристического полинома.

Критерий: для устойчивости линейной системы n-го порядка необходимо и достаточно, чтобы кривая Михайлова, построенная в координатах  , проходила последовательно через n квадрантов.

Критерий Найквиста

Критерий Найквиста — это графоаналитический критерий. Характерной его особенностью является то, что вывод об устойчивости или неустойчивости замкнутой системы делается в зависимости от вида амплитудно-фазовой или логарифмических частотных характеристик разомкнутой системы.

Пусть разомкнутая система представлена в виде полинома 

тогда сделаем подстановку   и получим: 

Для более удобного построения годографа при n>2 приведём уравнение (*) к «стандартному» виду: 

При таком представлении модуль A(ω) = | W(jω)| равен отношению модулей числителя и знаменателя, а аргумент (фаза) ψ(ω) — разности их аргументов. В свою очередь, модуль произведения комплексных чисел равен произведению модулей, а аргумент — сумме аргументов.

Устойчивость дискретных систем. Как и для систем непрерывного времени, под устойчивостью дискретной системы понимают ее способность возвращаться в положение равновесия после окончания действия внешних факторов. Рассматривается свободное движение управляемой системы, либо движение автономной системы при ненулевых начальных условиях.

Автономная система описывается уравнениями

a(z)y(k) = 0, a(z) = z_n + a_l z_n-1 + ... + a_n, y_y = y* = 0. (6.3.39)

Понятия устойчивости линейных дискретных систем практически полностью идентичны соответствующим понятиям непрерывных систем. Критерии устойчивости дискретных систем легко выводятся из соответствующих положений непрерывной теории, если принять во внимание, что полюсы z_i дискретной системы связаны с полюсами p_i эквивалентной непрерывной модели соотношением z_i = ехр(Тр_i). Поэтому ограничимся рассмотрением только свойства асимптотической устойчивости.

Устойчивость по выходу (техническая устойчивость) определяется характером изменения выходной переменной y(k), т. е. свойствами решений системы (6.3.39). Система называется асимптотически устойчивой, если выполняется условие

= 0.

Основной метод исследования устойчивости дискретных системы предусматривает использование корневых критериев. Дискретная система асимптотически устойчива тогда и только тогда, когда модули всех корней (полюсов) характеристического уравнения системы меньше 1, т.е. |z_i|<1, i=(1,n). Другими словами, полюсы системы на комплексной плоскости должны находиться внутри круга единичного радиуса, при этом окружность единичного радиуса является границей устойчивости. Наличие хотя бы одного корня вне единичного круга делает дискретную систему неустойчивой. Появление одного вещественного или пары двух комплексно-сопряженных корней на единичной окружности при условии расположения остальных корней внутри круга говорит о нейтральной устойчивости дискретной системы (устойчивости по Ляпунову).

Законы регулирования

Законом регулирования называют математическую зависимость, в соответствии с которой управляющее воздействие на объект вырабатывалось бы безынерционным управляющим устройством.

Многие из законов регулирования, реализуемых различными регуляторами релейного, импульсного действия, экстремальными и т. п., рассматриваются далее. Здесь ограничимся рассмотрением наиболее распространенных законов, реализуемых регуляторами по отклонению непрерывного действия. В этих простейших законах управляющее воздействие линейно зависит от отклонения, его интеграла и первой производной по времени.

 

В составе структуры САР содержится управляющее устройство, которое называется регулятором и выполняет основные функции управления путем выработки управляющего воздействия U в зави­симости от ошибки (отклонения), т. е. U = f(D). Закон регули­рования определяет вид этой зависимости без учёта инерционности элементов регулятора, а также устанавливает основные качественные и количественные характеристики систем.

Различают линейные и нелинейные законы регулирования. Кроме того, эти законы могут быть реализованы в непрерывном виде или в цифровом. Цифровые законы регулирования реализуются путем построения регуляторов с помощью средств вычислительной техники (микроЭВМ или микропроцессорных систем).

Рассмотрим основные линейные законы регулирования. Простейшим является пропорциональный закон, и регулятор в этом случае называют П-регулятором. При этом  , где   – посто­янная величина,  k – коэффициент пропорциональности. Основным достоинством П-регу­ля­тора является простота. По существу, это есть усилитель постоянного тока с коэффициентом усиления k. Недостатки П-регуляторазаключаются в невысокой точности регулирования, особенно для объектов с плохими динамическими свойствами.

Интегральный закон регулирования и соответствующий И-регу­лятор реализует следующую зависимость

,

где Т – постоянная времени интегрирования.

Техническая реализация И-регулятора представляет собой усилитель постоянного тока с емкостной отрицательной обратной связью.  И-регуляторы обеспечивают высокую точность в устано­вившемся режиме. Вместе с тем И-регулятор вызывает уменьшение устойчивости переходного процесса и системы в целом.

Пропорционально-интегральный закон регулирования позволяет объединить положительные свойства пропорционального и интегрального законов регулирования. В этом случае ПИ-регулятор реализу­ет зависимость

^.

Мощным средством улучшения поведения САР в переходном режиме является введение в закон регулирования производной от ошибки. Часто эта производная вводится в пропорциональный закон регулирования. В этом случае имеем пропорционально-дифференциальный закон регулирования, регулятор является ПD-регулятором, который реализует зависимость:

.

Кроме ПИ- и ПД-регуляторов, часто на практике используют ПИД-ре­гуляторы, которые реализуют пропорционально-интегрально-дифферен­циальный закон регулирования

.

Среди нелинейных законов регулирования наиболее распространены релейные законы. Существуют двухпозиционный и трехпозиционный законы регулирования. Аналитически двухпозиционный закон регулирования записывается следующим образом:

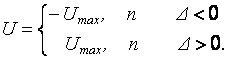
Трехпозиционный закон регулирования имеет следующий вид:

При трехпозиционном законе регулирования величина D_Н определяет зону нечувствительности регулятора.

Применение релейных законов позволяет при высоком быстродействии получить такие результаты, которые невозможно осуществить с помощью линейных законов.

В заключение дадим общую характеристику процессов, протекающих в системах автоматического управления. Как и в любой динамической системе, процессы в автоматической системе делятся на установившиеся и переходные.

При рассмотрении процессов в САУ важное значение имеют понятия "устойчивость системы", "качество процесса управления" и "точность управления".

Устойчивость – это свойство возвращаться в установившееся состояние после того, как она была выведена из этого состояния каким-либо возмущением. Такую устойчивость называют асимптотической или устойчивостью в точке. Замкнутые САУ весьма склонны к потере устойчивости, что чаще всего проявляется в возникновении расходящихся колебаний. В этом случае система становится неработоспособной.

В нелинейных системах большое значение имеет устойчивость в некоторой области, характеризующаяся возвратом в заданную область при уменьшении внешнего воздействия до нуля.

Качество процесса управления характеризуется тем, насколько процесс управления близок к желаемому.

Наибольшее применение в промышленности получили регуляторы непрерывного действия и позиционные (релейные) регуляторы. Регуляторы непрерывного действия могут быть классифицированы по закону регулирования. При этом под законом регулирования автоматического регулятора понимают закон изменения его выходной величины (регулирующего воздействия) в зависимости от изменения входной величины. По закону регулирования регуляторы непрерывного действия разделяют на пропорциональные (П-регуляторы), интегральные (И-регуляторы), пропорционально-интегральные (ПИ-регуляторы), пропорционально-дифференциальные (ПД-регуляторы), пропорционально-интегрально-дифференциальные (ПИД-регуляторы). Для формирования регулирующего воздействия регуляторы могут учитывать величину и знак отклонения регулируемого параметра от заданного значения ± Дф, интеграл отклонения по времени. Регуляторы, у которых отклонение регулируемого параметра от заданного значения вызывает перемещение регулирующего органа на величину, прямо пропорциональную отклонению, называются пропорциональными. Основным достоинством пропорциональных регуляторов является их быстродействие, т. е. малое время и высокая устойчивость процесса регулирования. Благодаря этим качествам П-регуляторы используют для работы с объектами без самовыравнивания. Недостатком П-регулятора является низкая точность регулирования, т. е. после окончания переходного процесса П-регуляторы не обеспечивают точно заданного значения регулируемого параметра. Разность между установившимся и заданным значениями регулируемого параметра при использовании П-регулятора называется остаточным отклонением. Интегральными регуляторами называются такие регуляторы, у которых скорость перемещения регулирующего органаt прямо пропорциональна сигналу рассогласования Дф. Достоинством И-регуляторов является то, что в установившемся режиме заданное значение регулируемого параметра поддерживается ими точно. Недостатками И-регуляторов являются их динамические свойства. Если появляется хотя бы небольшое отклонение регулируемого параметра от заданного значения, И-регулятор будет медленно перемещать регулирующий орган вплоть до положения его полного открывания или полного закрывания. Это может привести к увеличению сигнала рассогласования, т. е. к раскачиванию системы регулирования. И-регуляторы могут использоваться только для работы с объектами, обладающими большим самовыравниванием.

Роба́стное управле́ние — совокупность методов теории управления, целью которых является синтез такого регулятора, который обеспечивал бы хорошее качество управления (к примеру, запасы устойчивости), если объект управления отличается от расчётного или егоматематическая модель неизвестна. Таким образом, робастность означает малое изменение выхода замкнутой системы управления при малом изменении параметров объекта управления. Системы, обладающие свойством робастности, называются робастными (грубыми) системами. Обычно робастные контроллеры применяются для управления объектами с неизвестной или неполной математической моделью, и содержащими неопределённости.

Для проектирования робастных систем управления используются различные методы оптимального и робастного синтеза, среди которых синтез контроллеров в пространствах H∞ и H2, ЛМН-контроллеры, μ-контроллеры.

Главной задачей синтеза робастных систем управления является поиск закона управления, который сохранял бы выходные переменные системы и сигналы ошибки в заданных допустимых пределах несмотря на наличие неопределённостей в контуре управления. Неопределённости могут принимать любые формы, однако наиболее существенными являются шумы, нелинейности и неточности в знании передаточной функции объекта управления.

Метод пространства состояний (метод переменных состояния) основан на понятии "состояние системы". Состояние динамической системы описывается совокупностью физических переменных x_i(t), ..., x_n(t), характеризующих поведение системы в будущем при условии, если известно состояние в исходный момент времени и приложенные к системе воздействия.

В общем случае нелинейной системы, описание в переменных состояния имеет вид

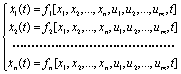. (6)

Если функции f₁, f₂, ..., f_n линейны относительно переменных x₁, x₂, ..., x_n, u₁, u₂, ..., u_n и не зависят от времени t, то их можно привести к виду

. (7)

В матричной форме выражение (7) имеет вид

. (8)

Такое выражение называется уравнением динамики для многомерной системы (u > 1), а в более компактном виде оно записывается через матричные операторы

. (8a)

где   и   вектор-столбцы содержащие все переменные состояния и входные сигналы соответственно;

A - матрица динамики (состояния) объекта или системы размерностью n x n , (n - размерность вектора x);

В — матрица управления (входа) размерностью n x m, (m — размерность вектора и), в случае одномерных систем матрица управления - вектор-столбец;

Для полного описания системы в пространстве состояний к уравнениям динамики (8) или (8 а) необходимо добавить уравнения, устанавливающие связи между переменными состояния x₁, ..., x_п и выходными переменными y₁, ...,y_r между входными u₁, ..., u_m сигналами и выходными переменнымиy₁, ...,y_r. Эта связь выражается в виде системы линейных алгебраических уравнений:

; (9)

или в векторно-матричной форме, называемой уравнением выхода

, (9a)

где   - матрица-столбец выходных сигналов системы;

C - матрица выхода размерностью r x n, (r - размерность вектора y), в случае одномерных систем матрица выхода - вектор строка;

;

D - матрица обхода (компенсации или усиления по входу), связывающая между собой входные и выходные сигналы. В реальных системах чаще всего такая связь отсутствует. Размерность матрицы обхода r x m. Для одномерных систем размерность матрицы обхода (1 x 1).

Для одномерных систем описание в пространстве состояний выглядит следующим образом

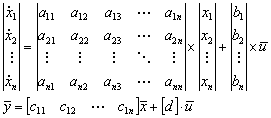. (10)

Таким образом, описание САУ в пространстве состояний выглядит как система двух уравнений в векторно матричной стандартной форме Коши

. (11)

Метод релаксации - итерационный метод решения систем линейных алгебраических уравнений.

Система линейных уравнений

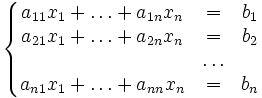
приводится к виду

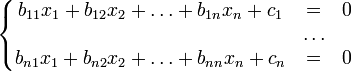
где  , 

Находятся невязки  :

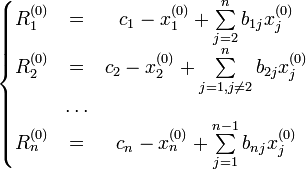
Выбирается начальное приближение  . На каждом шаге необходимо обратить в ноль максимальную невязку:  .

Условие остановки:  .

Ответ находится по формуле:  .

Решение систем линейных уравнений итерационными методами