1.5. Распределение потенциалов переноса

Ввиду малости толщины по­граничного слоя относительно характерного геометрического раз­мера (диаметр капли, пузыря и др.) считают, что можно пре­небречь переносом субстанции вдоль слоя по сравнению с по­перечным переносом этой субстанции, т. е, задачу можно считать одномерной, а пограничный слой, по той же причине,– плоским.

Найдем обшее и частное решения уравнения Лапласа, числен­ные значения и отношение градиентов и С для простейшего случая - плоского пограничного слоя. Будем его рассматривать как неограниченную плоскую пластину, для которой температура изменяется только в направлении оси х, перпендикулярной плос­кости пластины и изотермическим поверхностям.

С учетом сделанных замечаний уравнение (1-19) примет вид

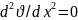(1.28)

Последовательным интегрированием получим общее решение уравнения:

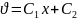(1.29)

Как видно, общее решение дает линейное распределение тем­пературы по оси х. Используя краевые условия (1.20), получим частное решение

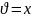
В этом случае

.

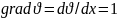Аналогичные выкладки с тем же результатом можно записать и для уравнения диффузии:

gradC=1.

Очевидно, что отношение градиентов также равно единице, что возвращает нас к соотношению (1-26).

Для сферических капель, пленок жидкости, пузырей газа из­менение температуры по радиусу в пограничном слое будет носить гиперболический характер:

где r = r/δ_о - координата относительной толщины слоя; R₁ = R₁/ δ_о , R₂ = R₂/δ_о - относительные внутренний и внешний ра­диусы слоя.

Найдем градиент функции :

(1.30)

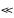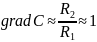Преобразуем уравнение (1-30) с учетом того, что δ_о R₁, r R₁ и соответственно R₂ = R₁ + δ_о ≈ R₁ получим . Аналогично: grad C ≈ 1, т.е. имеем тот же ре­зультат, который был получен в предыдущей задаче. Таким обра­зом, в пограничных слоях насыщенного и ненасыщенного газа не только отношение градиентов, но и сами градиенты равны или близки единице. Следовательно, изменение параметров среды при указанных условиях можно считать приближенно линейным.

Оценим (в процентах) степень нелинейности распределения температуры, взятую как относительную разность средней ариф­метической и действительной температуры в середине слоя, где отклонение близко к максимальному:

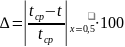
Примем зависимость теплопроводности от температуры линей­ной, так как она характерна для многих веществ, в том числе для газов и паров:

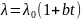
Интегрируя выражение плотности теплового потока

в пределах от х = 0 до любой текущей координаты х в интервале температур от t₁ до t₂ получаем распределение температуры в слое:

Удобно температуру на другой границе слоя принять равной t₂ = 0 (как точку отсчета температуры), чтобы получить простое выражение для Д (в процентах):

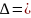
Подставляя численные значения Ь и найдем, что, например, для воздуха при t₁ – t₂ = 100°С Δ = 0,4%. В процессах тепло- и массообмена при непосредственном контакте воздуха и воды и атмосферном давлении разность температур на границах погра­ничного слоя насыщенного воздуха практически не превысит ука­занной разности, так как температура воды при данном давле­нии может меняться от 0 до 100 °С, а температура газа по смочен­ному термометру – в тех же пределах. Поэтому степень нелиней­ности распределения температуры в слое будет того же порядка. Ввиду ее незначительности можно считать распределение темпе­ратуры в слое линейным.

Рассмотрим распределение потенциалов переноса в погранич­ном с жидкостью слое газа. Для этого проследим тепло- и массо- обмен отдельно мелких и крупных капель воды в потоке воздуха, например, при t_ж < t_м. Температура мелких капель при контакте с воздухом быстро стремится к температуре воздуха по смочен­ному термометру Прогрев капель происходит через поверх­ность их пограничного слоя, температуру которое они в конечном счете и принимают, т. е. температура t_м на этой поверхности суще­ствует в течение всего процесса прогрева капель, как бы скоро­течен он ни был. При этом, поскольку температура t_м отвечает состоянию насыщения газа (t_м, d_м) то, естественно, она имеет место на границе насыщения, между слоем ненасыщенного и слоем насыщенного газа.

На крупных каплях процесс прогревания идет так же, как на мелких, через поверхность их пограничного слоя. Но они прогре­ваются медленнее из-за большой массы. При этом еще более тон­кий, чем пограничный, слой молекул пара, примыкающий к гра­нице насыщения газа, ввиду малости приходящегося на него количества влаги (G_м → 0) прогрегается почти мгновенно. В пограничном слое газ, пересекая границу насыщения, об­разует локальный расход G_сл, который может быть не равен общему расходу газа в аппарате. Поскольку отношение G_м/G_cл стремится к нулю, то имеют место условия, которые, по аналогии с процессами на мелких каплях, способствуют приобретению границей насыщения равновесного состояния (t_м, d_м) и сохранению этого состояния в течение всего процесса тепло- и массообмена.

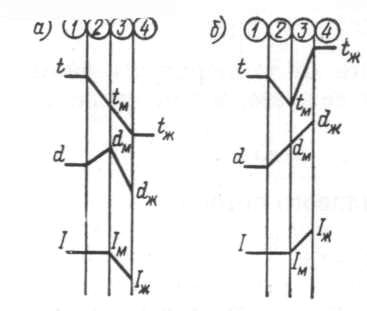
Рис. 1.1. Распределение потенциалов тепло- и массопереноса: а – охлаждение газа; б– нагре­вание газа; 1 – ядро потока газа; 2 – пограничный слой ненасы­щенного газа; 3 – пограничный слой насыщенного газа 4 – жидкость

Итак имеем: в ядре потока газа – параметры газа t, d и функ­цию состояния I на границе насыщения газа - соответственно t_м, d_м и I_м; на границе газа с жидкостью – t_ж, d_ж, I_ж Изменение этих параметров происходит в пределах соответствующих слоев ненасыщенного и насыщенного газа. Как указывалось выше, раз­личие между I и I_м невелико, поэтому в практических расчетах энтальпию можно считать постоянной. В графическом виде рас­пределение потенциалов переноса (температура, влагосодержание) и энтальпии газа в пограничном слое показано на рис. 1.1.

На границе газа с жидкостью в условиях фазового перехода имеет место скачок параметров: влагосодержание газа в жид­кости стремится к бесконечности, так как количество газа в жид­кости близко к нулю ввиду ее непроницаемости (относительной) для газа. Этот скачок влияет на распределение параметров, по­этому его нужно учитывать при определении влагосодержания d_ж. На границе насыщения газа наблюдаются экстремумы темпера­туры (рис. 1.1,6) и влагосодержания газа (рис. 1.1, а). В этих случаях течение потока переносимой массы (пара) под действием разности потенциалов через экстремум влагосодержания газа или соответствующего ему при данных условиях парциального давле­ния пара происходит в условиях взаимной компенсации равных долей движущих сил в слоях ненасыщенного и насыщенного газа, аналогично течению жидкости или газа в сообщающихся сосудах, каналах, объемах (течения в гидрозатворах, сифонах, зданиях и сооружениях при их аэрации, описываемые уравнением Бернулли). Переноса теплоты (полной) через экстремум температуры не происходит ввиду (как указывалось выше) постоянства энталь­пии в ненасыщенном газе.

Известно, что состояние влажного газа при данном давлении однозначно определяется его температурой t (сухого термометра) и влагосодержанием d или температурами сухого и смоченного термометров (t, t_м), или температурой смоченного термометра и влагосодержанием (t_м, d). За определяющие параметры в рас­чете теплообмена при наличии массообмена между жидкостью и ненасыщенным влажным газом можно выбрать любую из пере­численных пар параметров (для насыщенного состояния t = t_м и остается один параметр). Однако, как будет подробнее рассмот­рено в гл. 2, от выбора параметров зависит построение методики и алгоритм расчета, получение тех или иных расчетных зависи­мостей, их обобщение для возможно большего круга вопросов, связанных с расчетом тепло- и массообмена. Укажем, что в даль­нейшем будет использоваться последняя из названных пар пара­метров газа, а именно (t_м, d).

Кроме того, условия расчета также во многом зависят от того, какие разности параметров приняты зд определяющие.

Иногда при расчете процессов тепло- и массообмена, например, в контактных аппаратах кондиционирования воздуха, используют разности t – t_ж, d - d_ж [26]. Эти разности имеют ту особенность, что они могут менять свой знак в одном и том же процессе тепло- и массообмена. Например, разность d - d_ж меняет знак при на­греве воды от температуры ниже точки росы начального состоя­ния воздуха до температуры, которая меньше начальной темпе­ратуры воздуха по смоченному термометру, но больше темпе­ратуры точки росы. Это осложняет расчет, так как возникает необходимость в разделении реактивного пространства аппарата на отдельные участки и т. д. В то же время разности d_м - d и t_м – t_ж никогда не меняют знака и ими удобно пользоваться в расчетах. Другие разности, d_м - d_ж и t – t_м, тоже не меняют знака, но при определении d_ж необходимо учитывать дополнитель­ные условия (влияние скачка влагосодержания, изменение тем­пературы в пограничном слое жидкости и др.), а температура газа t не определяет его энтальпии. Разделение же и взаимо­увязка теплообмена по явной и скрытой теплоте делается обычно при упрощающих предпосылках об отсутствии указанного слож­ного распределения потенциалов в пограничном слое, что в ко­нечном итоге приводит к эмпирическим формулам и узким диа­пазонам их применения. Поэтому рекомендуется использование разностей d_м - d, t_м – t_ж.

Рассмотренное распределение потенциалов в пограничном с жидкостью слое газа может служить основой для построения модели, теоретического анализа и получения расчетных зависи­мостей процессов тепло- и массообмена.