Найдем dTw и dT из уравнений (2.5) и (2.6)

; .

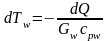Подставим dT_w и dT в уравнение (5.7):

.

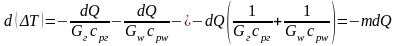откуда

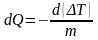. (2.8)

Подставим dQ из уравнения (2.8) в уравнение (2.4). После разделения переменных получим дифференциальное уравнение интенсивности теплообмена

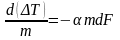. (2.9)

Обозначим поверхность контакта в теплообменнике через F_т, а средний температурный напор – через ΔT_т.

Проинтегрируем уравнение (2.9) по поверхности контакта F в пределах от F= = 0 до F = F_т и соответственно от ΔT = ΔT₀ до ΔT = ΔT_т, имея в виду, что средние за весь процесс α и m – вели­чины постоянные для рассматриваемого ряда теплообменников

.

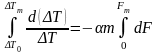После интегрирования получаем уравнение интенсивности теплообмена

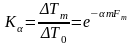. (2.10)

Для расчета явного теплообмена было бы достаточно уравне­ния (2.10) в совокупности с уравнениями теплового баланса и состояния сред, так как такая система уравнений является замк­нутой. Однако, для взаимосвязанных процессов тепло- и массо­обмена это уравнение не пригодно, так как в нем не отражено влияние массообмена на теплообмен. Вывод уравнений, в которых было бы это учтено, необходимо делать отдельно. При этом, алго­ритм вывода уравнения интенсивности теплообмена может быть взят за основу при выводе соответствующих уравнений интен­сивности массообмена и тепломассообмена для системы «вода–воздух».

2.3. Уравнение интенсивности тепломассообмена

Принимаем, что движущей силой тепломассообмена является разность температуры жидкости и температуры по смоченному термометру, а перенос теплоты от одной среды к другой характеризуется коэффициентом полного теплообмена (или коэффициентом тепломассообмена) σ (рис. 2.3).

В пределах бесконечно малого изменения поверхности контакта dF можно считать средние тем­пературы воздуха по мокрому термометру T_м и воды T_w постоянными. Поэтому, темпера­турный напор

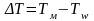. (2.11)

Бесконечно малое количество теплоты, которой обмениваются газ и жидкость в пределах dF, равно

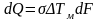. (2.12)

Температура газа уменьшается на dT_м, и он отдает эту теплоту:

. (2.13)

Температура жидкости увеличится на dT_w, и она воспринимает количество теплоты

. (2.14)

Дифференцируем уравнение (2.11):

.

Из уравнений (2.13) и (2.14) находим

; ,

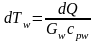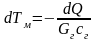и подставляем в уравнение (2.15):

.

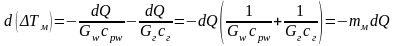где m_м– сумма обратных водяных эквивалентов сред.

Получим уравнение интенсивности тепломассообмена [1].

Отсюда

.

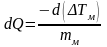Рис. 2.3. Графики средних за весь процесс тепломассообмена температур жидкости и газа в зависимости от площади поверхности контакта теплообменников: а – охлаждение воздуха; б – охлаждение воды.

После подстановки dQ в уравнение (2.12) и разделения переменных получим дифференциальное уравнение интенсивности тепломассообмена

.

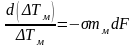Обозначим поверхность контакта в теплообменнике через F_т, а средний температурный напор – через ΔT_т.

Проинтегрируем уравнение (2.9) по поверхности контакта F в пределах от F = 0 до F = F_т и ,соответственно, от ΔT_м = ΔT_м0 до ΔT_м = ΔT_мт, имея в виду, что средние за весь процесс σ и m_м – вели­чины постоянные для рассматриваемого ряда теплообменников

.

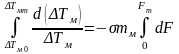Получаем уравнение интенсивности тепломассообмена

или

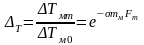. (2.16)

Коэффициенты Δ_T и

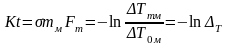
могут быть использованы в качестве определяемых чисел подобия, но удобнее в расчетах использовать числа подобия с меньшим количеством параметров сред. Поэтому, преобразовав уравнение (2.16) подставив вместо ΔT_мт выражение для среднелогарифмического температурного напора, вычисленное для противотока, получим выражение для коэффициента интенсив­ности тепломассообмена:

,

где 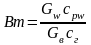– отношение тепловых эквивалентов жид­кости и газа.

Зная Km, по начальным параметрам сред можно определить конечную температуру газа по смоченному термометру, соот­ветствующую энтальпию газа, а следовательно, и количество пере­данной в аппарате теплоты, т.е. решить задачу тепломассообмена, не прибегая к расчету массообмена:

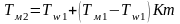. (2.17)

Коэффициент Km, в свою очередь, зависит от двух безразмерных величин

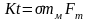и ,

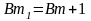т.е.

.

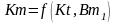Рассмотрим первое число подобия:

.

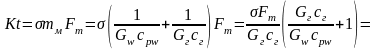
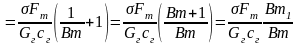Как видно, Kt зависит от двух идентичных чисел подобия Вm и Вm₁ одно из которых, а именно Bm₁, как более удобное при расчетах, будет использовано в качестве определяющего числа подобия.