1.3. Годограф вектор - функции

В механике для любой вектор-функции  , заданной и непрерывной на некотором промежутке времени  , вводится понятие ее годографа.

Определение 2

Годографом вектор-функции  называется геометрическое место точек в абсолютном пространстве, образованное концами векторов , имеющих своим началом точку отсчета  .

Очевидно, годограф вектор-функции  , задающей движение, совпадает с траекторией движения точки.

Понятие годографа чаще всего применяется к скорости движения точки (называется годографом скорости) и к ее ускорению (годограф ускорения).

Если известна скорость  материальной точки при всех , то для построения ее годографа:

• необходимо параллельным переносом совместить начало вектора скорости точки  с точкой отсчета  в каждый момент времени  ;

• геометрическое место концов построенного таким образом множества векторов при всех будет являться годографом вектора скорости  точки  .

Аналогично строится годограф ускорения  этой точки.

Годограф скорости  в трехмерном пространстве параметрически задается уравнениями

где

— координаты точек годографа скорости,

— координаты скорости материальной точки в момент времени .

Аналогично, для годографа ускорения  параметрические уравнения имеют вид

где

— координаты точек годографа ускорения,

— координаты ускорения материальной точки.

3º. Описание естественного способа задания движения

Суть естественного способа задания движения материальной точки такова: задается траектория и закон движения точки по этой траектории.

Математически этот способ задания движения описывается следующими действиями:

• задается регулярная кривая не ниже второй кратности (без особых точек) в естественной параметризации

; (1.2.5)

• задается закон движения по этой кривой

, (1.2.6)

где

— дважды непрерывно дифференцируемая функция, зависящая от  .

От естественного способа легко перейти к векторному способу задания движения точки, т. е. найти прямую связь естественного способа с векторным.

Векторный способ задания движения точки находится подстановкой закона движения (1.2.6) в уравнение траектории (1.2.5). В результате подстановки получим

. (1.2.7)

Соотношение (1.2.7) — это векторный способ задания движения.

Общая схема перехода от векторного способа задания движения к естественному способу (обратная связь) описана ниже в Дополнении 2 к §2 этой главы.

4º. Вычисление скорости и ускорения при естественном способе задания движения

4.1. Вычисление скорости

По определению скорости материальной точки можем записать

.

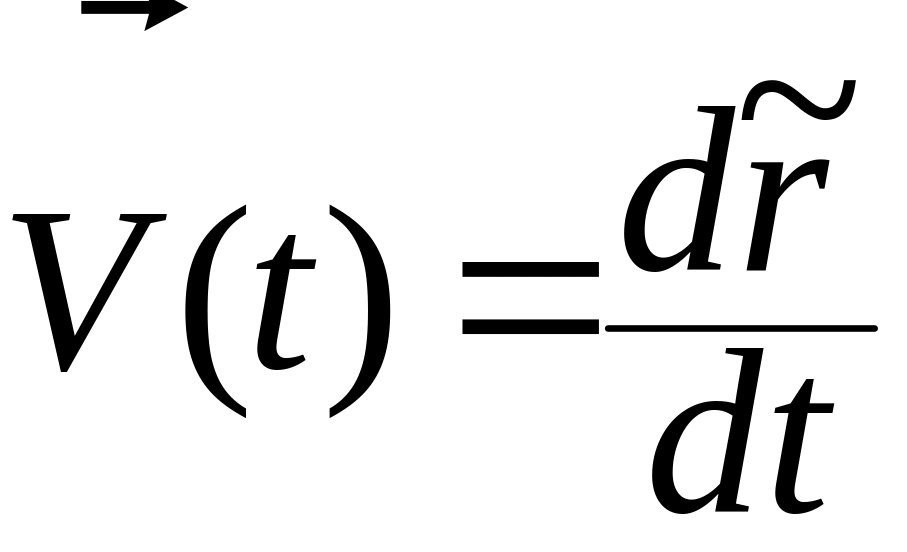Здесь

– движение точки  , заданное векторным способом;

– ее скорость в момент времени .

Согласно связи векторного способа с естественным имеем

,

где

– естественная параметризация траектории движения,

– закон движения по этой траектории.

Дифференцируя по , получаем

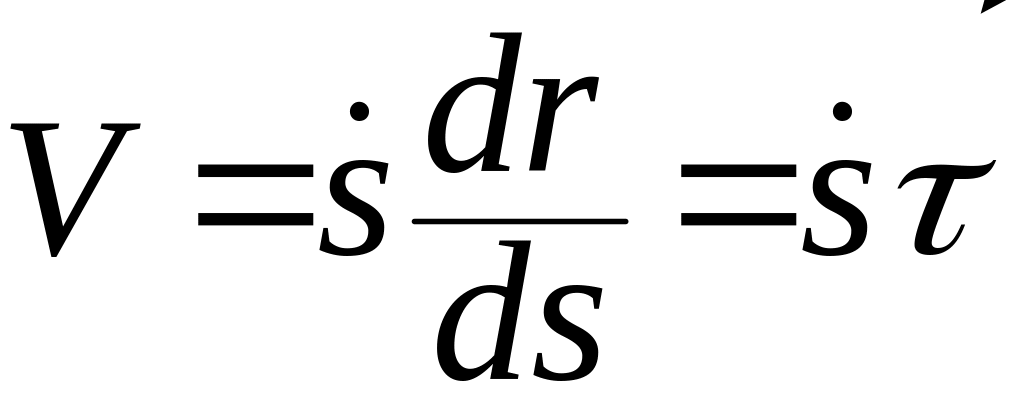, (1.2.15)

где

— орт касательной к траектории в той ее точке, с которой совпадает положение материальной точки в момент времени .

Из (1.2.15) можем сделать следующие заключения:

а) скорость параллельна — орту касательной к траектории в том положении точки , которое она занимает, находясь на траектории в момент времени ;

б) .