45

ЛЕКЦИЯ 2. КИНЕМАТИКА. Глава 1. (Лекция 1 по гл. 1) §1. Стр.1-22. §2. Стр.22-32. Доп.1-2. Стр.32-48. 31.07.2012

Глава 1. Кинематика точки

§1. Векторный и координатный способы задания движения точки

Как отмечалось во введении, кинематика решает задачу построения способов задания и описания движений и способов вычисления их кинематических характеристик.

Решение данной задачи не связывается с причинами, по которым возникают движения. А потому в кинематике не делается различий между материальной и геометрической точкой.

При этом, как было отмечено в п.1º §4 Введения, под положением материальной точки относительно заданной точки отсчета в фиксированный момент времени понимается положение той геометрической точки в евклидовом пространстве, с которой материальная точка совпадает в указанный момент времени.

Движением материальной точки, согласно определению 3 из п.3º §4 Введения, называется дважды непрерывно дифференцируемая вектор-функция  , значения которой в каждый момент времени соответствует положению материальной точки, которое она занимает в этот момент.

1º. Векторный способ задания движения точки

1.1. Описание векторного способа задания движения

Из определения 3 (п.3º §4 Введения) вытекает, что для того, чтобы задать движение материальной точки, необходимо:

1. выбрать точку отсчета (обозначим ее ),

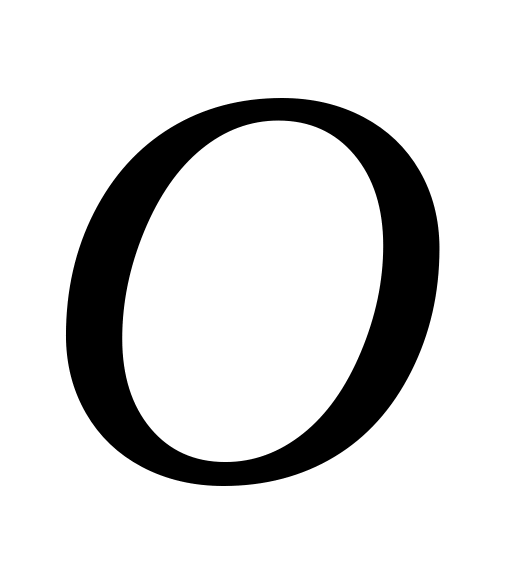2. задать вектор-функцию на том промежутке времени, где хотим знать о движении, причем вектор-функция должна быть дважды непрерывно дифференцируема по ,

3. задать положение точки в момент времени относительно точки отсчета равенством

, (1.1.1)

где

— радиус-вектор той геометрической точки абсолютного пространства, с которой в момент времени по своему положению совпадает материальная точка  .

Таким образом, на равенство (1.1.1) можем смотреть, как на способ задания движения материальной точки. Такой способ называется векторным заданием движения точки.

1.2. Вычисление скорости и ускорения при векторном способе задания движения

Из (1.1.1) согласно определениям скорости и ускорения вытекает, что скорость и ускорение точки при известном ее движении вычисляются по формулам

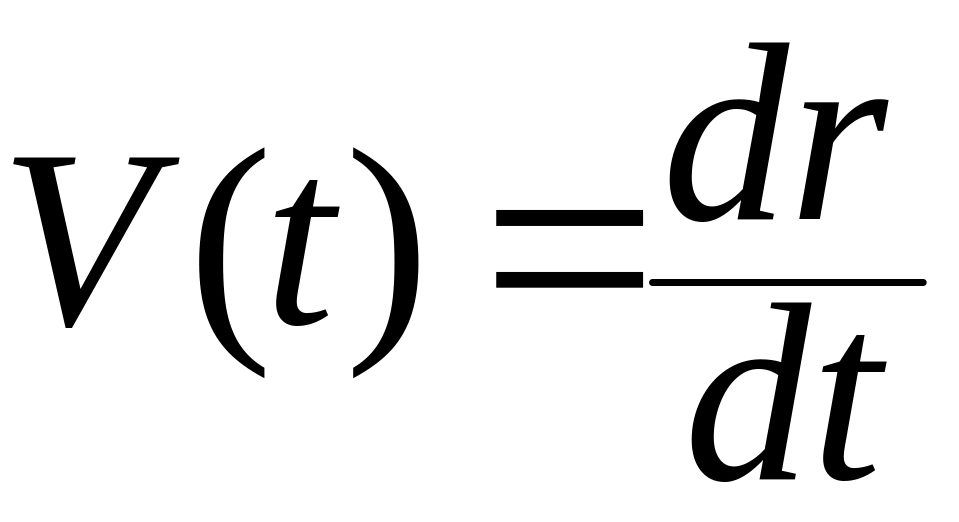, . (1.1.2)

Заметим, что векторы и , задаваемые формулами (1.1.2), имеют своим началом геометрическую точку  , которая служит концом радиус-вектора  , устанавливающего положение материальной точки в момент времени .

1.3. Построение движения по заданной скорости

Соотношение (1.1.1):

, (1.1.1)

— это векторный способ задания движения, позволяющий определить положение точки в любой момент времени .

Соотношение (1.1.2):

, . (1.1.2)

— это способ вычисления недостающих кинематических характеристик в этот момент (скорости и ускорения материальной точки) по заданному движению.

Однако движение может быть определено и в том случае, когда задана скорость или ускорение материальной точки на том промежутке времени, на котором необходимо знать о движении.

Действительно, если в любой момент времени  задана скорость , то имеем

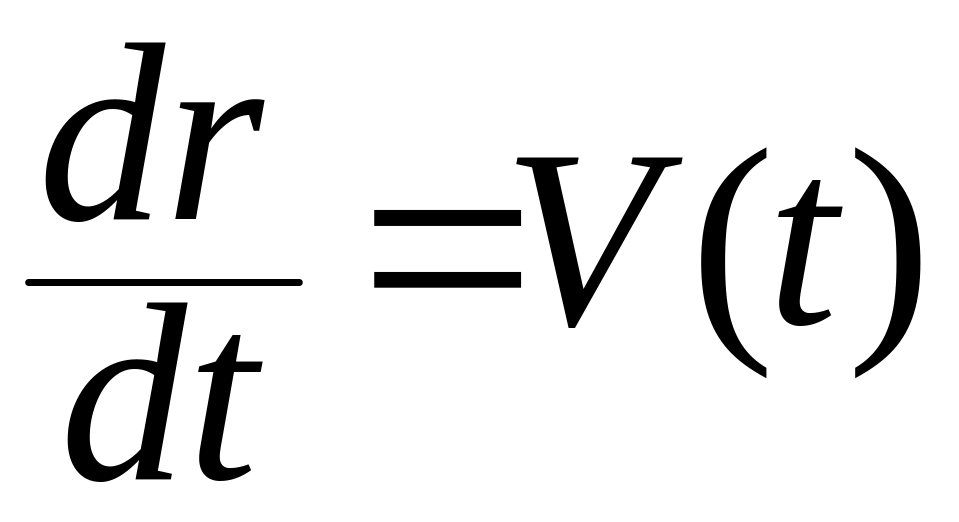. (1.1.3)

Справа стоит известная вектор-функция . Слева — вектор-функция , определяющая движение точки, является неизвестной.

На формулу (1.1.3) можем смотреть, как на уравнение для определения движения.

Из него следует, что является первообразной для функции , а потому

. (1.1.4)

Здесь — некоторый постоянный вектор, а — первообразная функция вектор-функции .

Соотношение (1.1.4) задает семейство движений, каждое из которых имеет в любой момент времени  заданную скорость .

Чтобы из формулы (1.1.4) выделить конкретное движение, проходящее через заданную геометрическую точку с радиус-вектором при , надо положить в (1.1.4) слева и .

Тогда получим

,

где — значение первообразной в момент .

Выразив отсюда , найдем

.

Поскольку

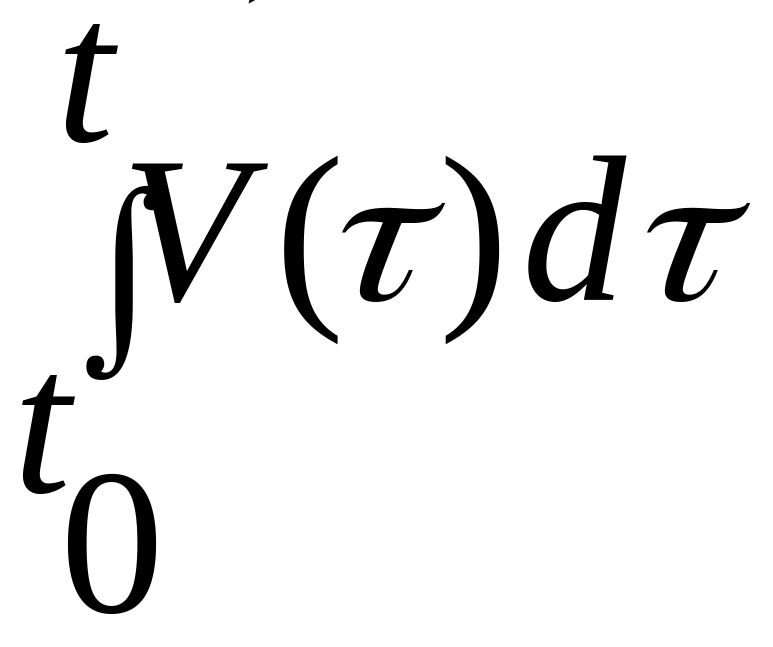
— это определенный интеграл от векторной функции , то можем записать

. (1.1.5)

Формула (1.1.5) – это векторная форма определения движения точки при задании ее скорости как функции времени.