Нечеткое включение и нечеткое равенство множеств. Продолжение

Определение. Степень равенства двух нечетких подмножеств множества Х определяется как:

.

• Если , то множества нечетко равны .

• Если , то множества нечетко не равны .

• Если , то множества взаимно индифферентны .

Примечание:

Понятия нечеткого равенства и неравенства, индифферентности являются обобщением понятий равенства и неравенства для четких множеств. Действительно, пусть А и В – четкие множества, тогда в случае А=В, , если же А ≠ В и .

Определение. Нечеткое множество А равно нечеткому множеству В – А=В, если .

Нетрудно заметить, если выполняется равенство множеств А=В, то эти множества являются и нечетко равные .

Нечеткое включение и нечеткое равенство множеств. Пример

На универсальном множестве футбольных клубов РФПЛ Y определим нечеткое множество «богатый клуб»:

Теперь выясним, как соотносятся между собой нечеткие множества «надежная оборона» и «богатый клуб»:

Вывод: Необязательно, что понятие «богатый клуб» обеспечивает включение понятия «надежная оборона»:

• одновременно нечетко включается и нечетко не включается в 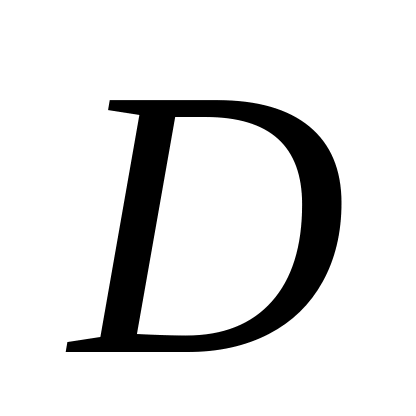( и );

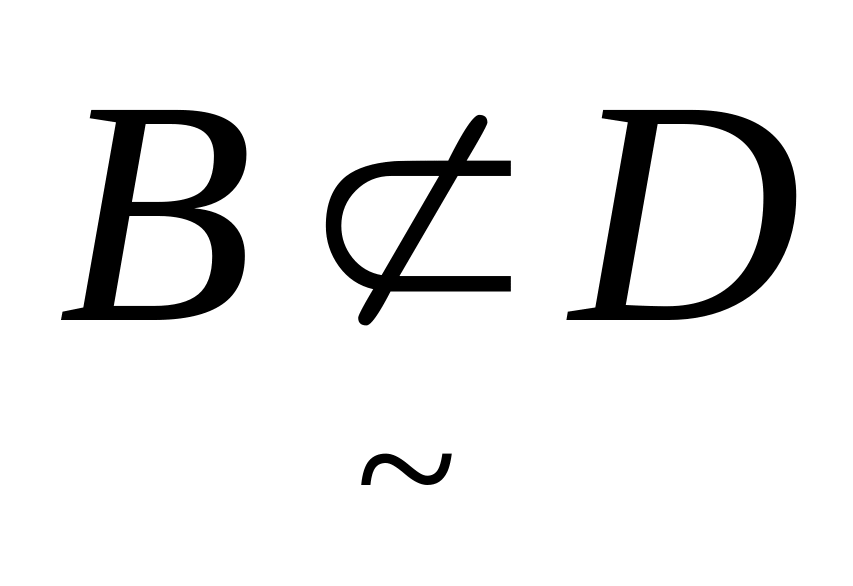• нечетко включается ( );

• и взаимно индифферентны ( ).

Теоретико-множественные операции над нечеткими множествами

Классическая теория множеств	Нечеткие множества
Пересечение множеств ; Объединение множеств ; Отрицание (дополнение) множества .	Заде предложил аналогичный набор через операции с функциями принадлежности: Пусть А <=> А(x), В <=> В(x), тогда результатом теоретико-множественной операции будет нечеткое множество С<=>С(x), причем: если С = А  В, то: С(x) = min(А(x), В(x)); если С = А  В, то: С(x) = max(А(x), В(x)); если С = , то: С(x) = 1 - А(x).

Теоретико-множественные операции над нечеткими множествами. Пример

На универсальном множестве действительных чисел от 0 до 80, определяющем возраст человека, введем нечеткое множество «тренер на пике карьеры»:

Н ечеткое множество «Тренер молодой И на пике карьеры»:

С = А  В

Нечеткое множество «Тренер молодой ИЛИ на пике карьеры»:

С = А  В

Теоретико-множественные операции над нечеткими множествами. Пример. Окончание

Нечеткое множество «НЕ молодой тренер»:

С =

Примечания:

В отличие от четких множеств, для нечетких множеств в общем случае: и .

Пусть А, В, С – нечеткие множества, тогда выполняются следующие свойства:

1. Коммутативность:

2. Ассоциативность:

3. Идемпотентность:

4. Дистрибутивность:

5. Законы де Моргана:

Дополнительные операции над нечеткими множествами

Определение. Пусть A нечеткое множество с функцией принадлежности _А(x), тогда результатом операции возведения в степень , где  – положительное число, будет нечеткое множество A^, характеризующееся функцией принадлежности: .

Примечание:

Частным случаем возведения в степень являются:

• CON(A) = A² – операция концентрирования,

• DIL(A) = A^0,5 – операция растяжения.

Пример. Для нечеткого множества «Надежная оборона» применим операции концентрирования и растяжения: