Примеры Нечетких множеств

Предметная область знаний – Российская футбольная Премьер-Лига (РФПЛ)

1). Рассмотрим термин «Надежная оборона». Представим его в виде нечеткого множества:

• Пусть Х – множество действительных чисел в промежутке от 0 до 3, определяющее значение показателя среднее количество пропущенных мячей за матч;

• Тогда на Х можно определить нечеткое множество А («Надежная оборона») с функцией принадлежности типа:

Примечание:

• Вид функции принадлежности может быть абсолютно произвольным. Основные виды:

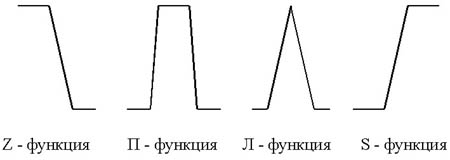
Примеры Нечетких множеств. Продолжение

Замечание:

Теперь, зная значения показателя среднего количества пропущенных мячей за матч для конкретных клубов РФПЛ в данный момент времени:

Клуб	Зенит	ЦСКА	Спартак	Анжи	Кубань	Амкар
Показатель	0.8	1.0	1.2	1.1	0.9	1.3

можно тем самым представить тот же термин «Надежная оборона» в виде нечеткого множества B, определенного уже на новом универсальном множестве Y футбольных клубов РФПЛ:

Примеры Нечетких множеств. Продолжение

2). Рассмотрим термин «Молодой главный тренер». Представим его в виде нечеткого множества:

• Пусть X – теперь множество действительных чисел в промежутке от 0 до 80, определяющее возраст человека;

• Тогда на X можно определить новое нечеткое множество A («Молодой главный тренер») с функцией принадлежности типа:

Примечание:

Учитывая специфику тренерской работы, главного тренера в возрасте до 35 лет следует считать скорее юным тренером, чем молодым.

Примеры Нечетких множеств. Окончание

3). Рассмотрим термин «Точечная селекция». Представим его в виде нечеткого множества:

• Пусть Х – множество натуральных чисел;

• Тогда на Х можно определить нечеткое множество «Точечная селекция» следующим образом:

Определение. Носителем нечеткого множества А называется подмножество множества Х, содержащее те элементы из Х, для которых значения функции принадлежности .

Для последнего примера носителем нечеткого множества S является множество .

– это обычное четкое подмножество множества натуральных чисел.

Нечеткое включение и нечеткое равенство множеств

Определение. Пусть заданы два нечетких подмножеств множества Х. Степень включения (нечеткого множества А в нечеткое множество В) находится по формуле:

.

• Если , то нечеткое множество А нечетко включается в нечеткое множество В и обозначается .

• Если , то нечеткое множество А нечетко не включается в нечеткое множество В и обозначается .

Определение. Нечеткое множество A включается в нечеткое множество B – , если .

Примечание:

Справедливо следующее утверждение: если А включается в В, то выполняется и нечеткое включение . Но, если же выполняется , то из этого не следует, что .