Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Новосибирский государственный технический университет»

Факультет бизнеса

Кафедра экономической информатики

Расчетно-графическая работа

по дисциплине «Математическое моделирование»

Вариант №16

Выполнил:

Группа: ФБИ – 22.

Преподаватель: Соболева О.Н.

Новосибирск 2015

Содержание

1.Задание №1. 3

2.Задание №2. 5

3.Задание №3. 12

1. Задание №1.

Цены двух видов товаров равны соответственно 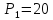и денежных единиц. Определить, при каких количествах x и y продаж этих товаров прибыль будет максимальной, если функция издержек имеет вид

.

Решение:

Сумма оборотов 1 и 2 видов товаров записывается следующим образом:

.

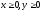Запишем целевую функцию – сумма оборотов двух видов товаров за вычетом издержек: , при ограничениях и x, y – целые числа, т.е. .

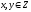В среде приложения MatLab, создадим скрипт для целевой функции, который изображен на рисунке 1.

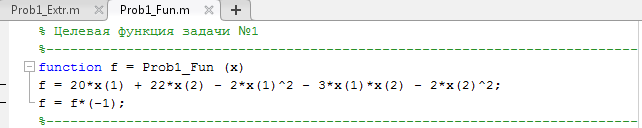
Рисунок 1 – Функция Prob1_Fun

Текст головной программы с использованием функции fminsearchпредставлен на рисунке 2.

Рисунок 2 – Головная программа для функции fminsearch

Результат выполнения головной программы представлен на рисунке 3.

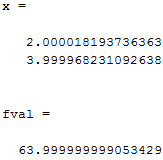
Рисунок 3 – Результат работы функции fminsearch

Второй вариант решения предполагает использование функции quadprog. Необходимым условием применения данной функции является возможность представления целевой функции в следующей матричной записи:

.

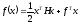Для нашей задачи:

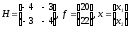
Ввод данных коэффициентов для матриц и использование функции quadprogпривидены на рисунке 4.

Рисунок 4 – Головная программа для функции quadprog

Результат выполнения головной программы представлен на рисунке 5.

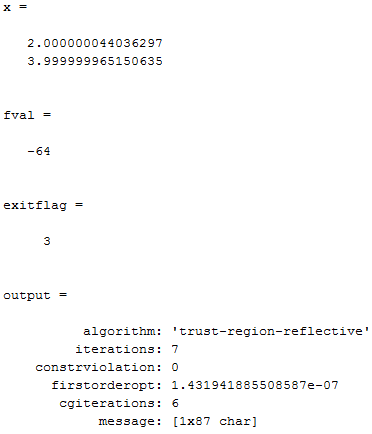
Рисунок 5 – Результат работы функции quadprog

В заключении необходимо домножить значение целевой функции на (-1). Действительно, полученные результаты полностью согласуются с ручными вычислениями:

Условие наличия в точке максимума: – выполняется.

Вычисление значения целевой функции в точке :

Ответ: усл. ед.

2. Задание №2.

Предположим, что для изготовления продукции P1 и P2 требуется использование трех видов ресурсов R1, R2, R3. Количество ресурсов и нормы их расхода на изготовление единицы каждого вида продукции известны и задаются в таблице 1.

Таблица 1 – Нормы расхода ресурсов на изготовление каждого вида продукции

Виды ресурсов	Количество ресурсов	P1	P2
R1	37
R2	70	1	2
R3	35	2	2

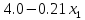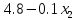Прибыль, получаемая предприятием от реализации единицы продукции P1 и P2, составляет соответственно и денежных единиц. В задаче требуется составить такой план выпуска продукции видов P1 и P2, при котором прибыль предприятия от реализации всей продукции оказалась бы максимальной.

Решение:

Составим математическую модель задачи:

Скрипт для целевой функции и скрипт для нелинейных ограничений в среде MatLabпредставлены на рисунках 6 и 7 соответственно.

Рисунок 6 – Функция Prob2_Fun

Рисунок 7 – Функция Prob_Nonlin

Аналитическое решение задачи произведено с помощью функции fmincon. Головная программа представлена на рисунке 8.

Рисунок 8 – Головная программа для функции fmincon

Результат выполнения головной программы представлен на рисунке 9.

Рисунок 9 – Результат работы функции fmincon

В заключении необходимо домножить значение целевой функции на (-1).

Графическое решение данной задачи можно разделить на следующие этапы:

1. Построение ОДР задачи.

2. Построение линий уровня целевой функции.

3. Определение, находится ли максимум целевой функции внутри ОДР. Вычисление значения целевой функции – искомый результат.

4. Определение точки касания границы ОДР и линии уровня.

5. Нахождение координат точки касания.

6. Вычисление значения целевой функции в точке касания – искомый результат.

Текст скрипта графического решения задачи представлен на рисунке 10.

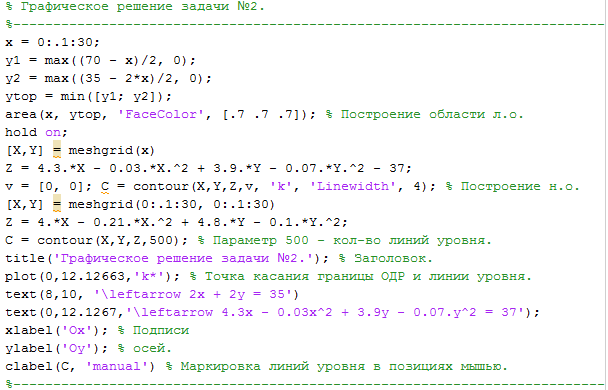
Рисунок 10 – Скрипт для графического решения задачи

Результат графического решения задачи представлен на рисунке 11.

Рисунок 11 – Графическое решение задачи №2

Анализ рисунка №2 позволяет сделать ряд следующих выводов:

1. Глобальный максимум целевой функции не принадлежит ОДР.

2. Граница ОДР задана единственным графиком неявной функции .

3. Целевая функция принимает свое наибольшее значение в точке касания границы ОДР и линии уровня (Z≈ 43,5).

Для определения координат точки касания необходимо произвести увеличение 1-ой координатной четверти в месте непосредственного касания. Касание границы ОДР и линии уровня (Z≈ 43,5) представлено на рисунке 12.

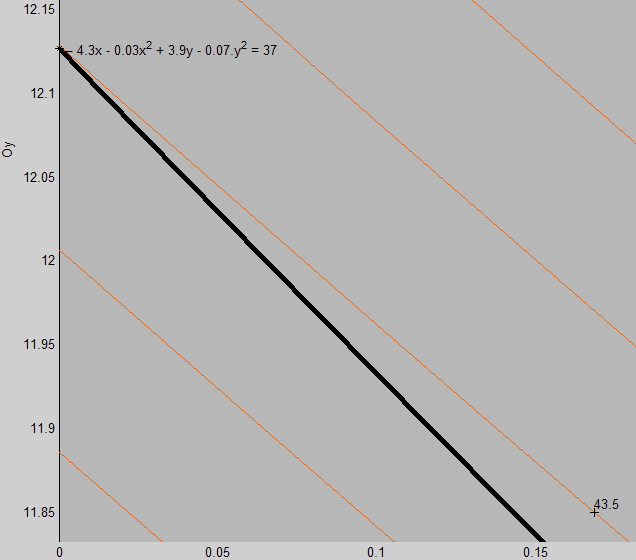
Рисунок 12 – Точка касания граничной кривой и линии уровня (Z= 43,5)

Следовательно, . Решение, полученное графическим способом, согласуется с результатом аналитических вычислений.

Однако решаемая задача является задачей целочисленного линейного программирования (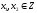), соответственно необходимо произвести округление полученного результата до целых в меньшую сторону: .

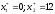Значение целевой функции равно: 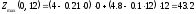усл. ед.

Ответ: 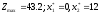усл. ед.