4.2. Розрахунок простої підвіски

При розрахунках приймають наступні|слідуючі| допущення: контактний провід|провід| в прольоті є абсолютно гнучка нитка, тобто маса проводу|проводу| рівномірно розподілена не по його довжині|проводу|, а по довжині прольоту.

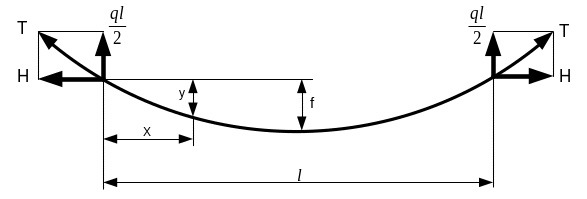
Рис. 4.2 – Схема розрахунку простої підвіски

Стрілу провисання проводу|проводу| «у» в точці|точці|, розташованій|схильній| на відстані «х» від опори (рис.4.2), визначають з виразу|вираженню|:

. (4.6)

Максимальна стріла провисання має місце у середині прольоту, тобто при x=l/2, тоді

, м. (4.7)

Тяжіння проводу|проводи| визначають|ся| за формулою [1,4]:

, Н. (4.8)

Реакція в опорі від навантаження «q» на багато менше горизонтальної складової Н, тобто .

Тому в середині прольоту можна прийняти .

Рівняння стану проводу|проводу| встановлює залежність між натягненнями проводів|проводів| у прольоті при двох різних режимах.

Нехай|нехай| початковий|вихідний| режим, параметру якого присвоєний індекс 1, характеризує натягнення Н₁, температура t₁, питоме навантаження q₁; шуканий режим з|із| індексом і характеризує тяжіння| Н_і, температура t_і і навантаження q_і.

Рівняння стану для цих двох режимів має вигляд|вид| [1]:

, (4.9)

де – питомі навантаження відповідно до початкового|вихідного| й шуканого

режимів, Н/м;

– горизонтальні складові тяжіння| проводів|проводів|, Н;

l – довжина прольоту, м;

– температура, відповідно початкового|вихідного| й шуканого режимів °С;

α – температурний коефіцієнт лінійного розширення;

Е – модуль пружності, МПа|;

S – площа|майдан| перерізу проводу|проводу|, мм².

При зміненому навантаженні на проводі|проводі| рівняння стану вирішують|рішають| щодо|відносно| температури i-го режиму, задаючись значеннями Н_і.

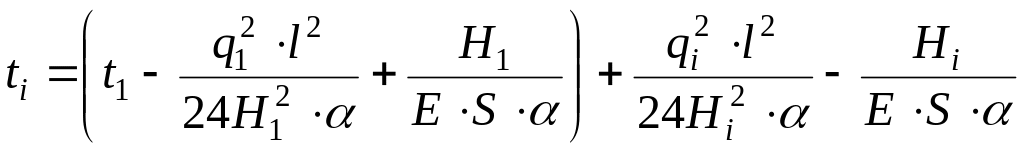, ^оС. (4.10)

Якщо анкерний проліт L_а складається з прольотів різної довжини, то в рівняння стану підставляють значення еквівалентного прольоту, в якому від дії температури і навантажень виникають ті ж тяжіння|, як і в багатопролітній підвісці в цілому|загалом|.

, м. (4.11)

Для визначення початкового|вихідного| режиму (тобто режиму з|із| індексом 1) необхідно знайти величину критичного прольоту l_кр.

, м. (4.12)

Критичний проліт - це такий проліт, в якому тяжіння| проводу|проводу| в режимі ожеледиці і в режимі мінімальної температури – однакові й дорівнюють допустимому. Якщо реальний проліт менше критичного, то початковий|вихідний| режим буде режимом мінімальної температури, якщо реальний проліт більший за l_кр, то початковий|вихідний| режим – режимом ожеледиці.

Порядок|лад| розрахунку простої підвіски:

1. Визначають навантаження q для чотирьох розрахункових режимів.

2. Визначають допустиме тяжіння| проводів|проводи| за таблицями або за формулою (4.7).

3. Знаходять|находять| еквівалентний проліт .

4. Визначають критичний проліт .

5. Порівнюючи l_кр і l_екв, визначають початковий|вихідний| режим||ви.

6. Складають рівняння стану і вирішують|рішають| його щодо|відносно| t_i.

7. Будують залежності H(t) і f(t) – монтажні криві (рис.4.4 ).

4.2.1. Розрахунок маятникової системи

Рис.4.3 - Геометрія маятникової підвіски: Л – довжина проекції на горизонтальну площину проводу в прольоті з урахуванням зігзагообразності його розташування в плані, м; L – реальна довжина проводу в прольоті, м; l – відстань між точками підвісу проводів, вимірювана уздовж осі шляху, м; γ - кут нахилу струни; λ – довжина струни маятникової підвіски; Q – вертикальна складова навантаження від ваги підвіски (враховується Q = q·l).

У маятниковій підвісці від натягнення контактного проводу змінюються нахил струн і, отже, розрахункова (реальна) довжина прольоту Л (рис.4.3). З геометрії підвіски виходить, що:

Л =

Але, внаслідок крихти приватного с² / l² в порівнянні з одиницею можна з достатньою точністю вважати, що

Л = l·(1 + )

Рівняння стану проводу|проводу|, яке вирішується|рішається| щодо|відносно| температури i-го режиму, має вигляд:|вид|

(4.13)

Одержаний вираз (4.13) відрізняється від рівняння полягання простої підвіски тільки наявністю різниці с_і² – с₁² / 2 l². Але, окрім невідомого Н_і, рівняння містить невідому величину с_і. Необхідно знайти залежність між Н і «с», користуючись геометричним співвідношенням (рис.4.3). З проекції підвіски на площину, перпендикулярну її осі, маємо

В = 2·а₁ + с_1;

а₁ = (В – с₁) / 2.

Тут «с₁» беруть з|із| геометрії маятникової системи (рис.4.3), а за початковий|вихідний| режим – режим мінімальної температури.

Щоб вирішити|розв'язати| дане рівняння, необхідно побудувати|спорудити| Н(с) відповідно до виразу:|вираження|

, Н. (4.14)

Величину «В» визначають за умови максимального натягу| КП| в режимі мінімальної температури.

, м. (4.15)

Тут задаються довжиною струн «λ» і максимальним кутом|рогом,кутком| відхилення струни «γ». Стрілу підвісу підвіски знаходять за|лічит формулою:

. (4.16)

За формулою (4.13) будують монтажні криві (рис. 4.4).

	На рис.4.4 пунктирні лінії - для простої підвіски, суцільні лінії - для маятникової підвіски при однаковій довжині прольоту. Звідси видно, що для маятникової підвіски при високих температурах натягнення значно вище.
Рис. 4.4 - Монтажні криві