
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Расчетно-графическая работа
по дисциплине «Численные методы»
Вариант № 29
Выполнил:
Студент
Группа ФБИ-22
Факультет Бизнеса
Преподаватель: Соболева О.Н.
Новосибирск 2014
Задание 1
Запишите порядок выполняемых вами операций, оцените погрешности их результатов, вычислите и запишите искомое значение. Определите число верных знаков.
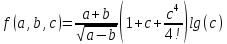
a=0.02456±0.00005; b=0.01823±0.00005; c=0.348±0.001

 -
точное значение
-
точное значение
 -
приближенное значение
-
приближенное значение
Δx-абсолютная погрешность
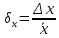 -
относительная погрешность
-
относительная погрешность
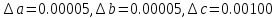
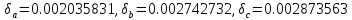
Порядок выполняемых операций:
Находим абсолютную и относительную погрешности
-
(1+c);
-
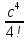 ;
; -
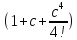 ;
; -
(a+b)
-
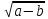
-
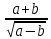
-
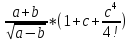 ;
; -

-
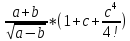 *
*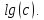
Воспользуемся универсальными оценками:
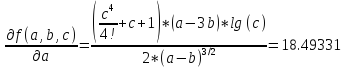
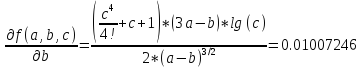
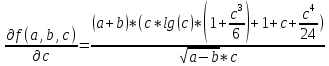 = 1.83595962
= 1.83595962
Предельная абсолютная погрешность:
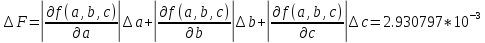
 F=
F=
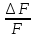 = 0.008814431
= 0.008814431
Определение числа верных знаков:
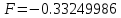 ;
;
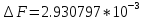 ;
;

6: 5*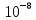 < 2.9308*
< 2.9308*
8: 5*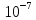 < 2.9308*
< 2.9308*
9: 5*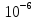 < 2.9308*
< 2.9308*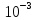
9: 5*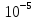 < 2.9308*
< 2.9308*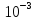
4: 5* < 2.9308*
< 2.9308*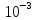
2:
5*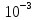 > 2.9308*
> 2.9308*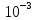
3:
5*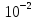 > 2.9308*
> 2.9308*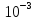
3:
5*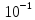 > 2.9308*
> 2.9308*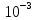
Следовательно 2, 3, 3 верные цифры.
Ответ: m=3,
F=-3.3249986*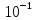 .
.
Задание 2
Выясните погрешность задания исходных данных, необходимую для получения результата с m верными значащими цифрами
m=5, a=0.02456; b=0.01823; c=0.348.
Полагаем верными 5 цифр, тогда
Относительная
погрешность
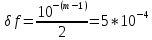
Абсолютная
погрешность
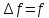 *
*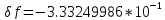 *
*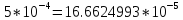
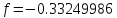 ;
;
a*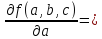 0.02456*
0.02456*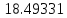 =
0.45419569
=
0.45419569
b*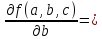 0.01823*
0.01823*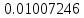 =
0.0001836209
=
0.0001836209
 0.348*1.83595962
= 0.63891395
0.348*1.83595962
= 0.63891395
a* b*
b*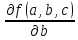 +
+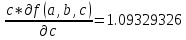
Допустимая погрешность данных
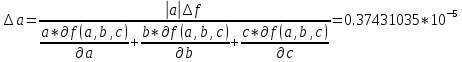
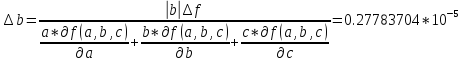
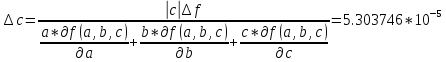
Задание 3
Решить СЛАУ методом Гаусса и с точностью ε=0,001 методом простой итерации.
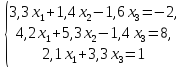
Метод Гаусса:
Перепишем систему уравнений в матричном виде:
A=
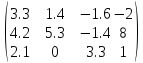
Первую строку делим на 3.3:
A=
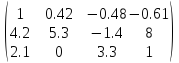
От второй и третьей строк отнимаем первую строку, умноженную на 4.2 и 2.1 соответственно:
A=

Вторую строку делим на 3.536:
A=
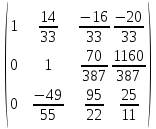
Третью
строку делим на -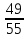 :
:
A=
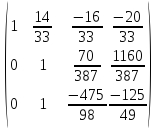
Из 3 строки вычитаем 2:
A=
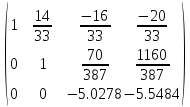
Третью строку делим на -5.0278:
A=
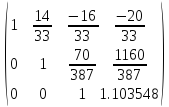
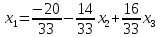
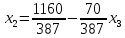
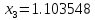
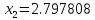
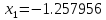
Ответ:
Х=

Метод простой итерации:
Приводим исходную матрицу к матрице с диагональным преобладанием
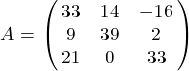 ,
, 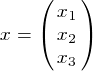 ,
, 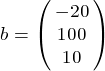 .
.
Преобразуем
исходную систему ![]()
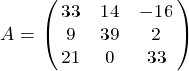 ,
, 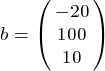
к виду x=Bx+φ.
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,![]() ,
,
![]() ,
, ![]()
Тогда
получим
B=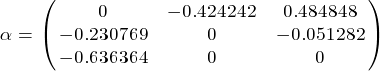 ,
φ=
,
φ=
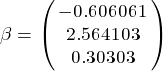
При этом норма матрицы ǁBǁ=0.909091 < 1, следовательно, достаточное условие выполняется.
Зададим
X(0)=φ= .
.
X(1)=BX(0)+φ= *
* +
+
 =
=
 .
.
Ɛ (1) = ǁ X(1)-X(0)ǁ=0.940877 > Ɛ.
X(2)=BX(1)+φ= *
* .+
.+
 =
=
 .
.
Ɛ (2) = ǁ X(2)-X(1)ǁ=0.598741 > Ɛ.
X(3)=BX(2)+φ=
 .
.
Ɛ (3) = ǁ X(3)-X(2)ǁ=0.206575 > Ɛ.
X(4)=BX(3)+φ=
 .
.
Ɛ (4) = ǁ X(4)-X(3)ǁ=0.131457 > Ɛ.
X(5)=BX(4)+φ=
 .
.
Ɛ (5) = ǁ X(5)-X(4)ǁ=0.045371 > Ɛ.
X(6)=BX(5)+φ=
 .
.
Ɛ (6) = ǁ X(6)-X(5)ǁ=0.028873 > Ɛ.
X(7)=BX(6)+φ=
 .
.
Ɛ (7) = ǁ X(7)-X(6)ǁ=0.009768 > Ɛ.
X(8)=BX(7)+φ=
 .
.
Ɛ (8) = ǁ X(8)-X(7)ǁ=0.006216 > Ɛ.
X(9)=BX(8)+φ=
 .
.
Ɛ (9) = ǁ X(9)-X(8)ǁ=0.002062 > Ɛ.
X(10)=BX(9)+φ=
 .
.
Ɛ (10) = ǁ X(10)-X(9)ǁ=0.001312 > Ɛ.
X(11)=BX(10)+φ=
 .
.
Ɛ (3) = ǁ X(3)-X(2)ǁ=0.000427 < Ɛ, следовательно, решение с заданной точностью найдено.
Ответ:
X=
 .
.
Задание 4
Методом вращения с точностью ε=0,00001 вычислить собственные значения и собственные векторы симметрической матрицы А.

Максимальный
по модулю наддиагональный элемент
равен ![]()
Определим угол поворота
![]()
![]()
![]()
Тогда матрица поворота H(0) определяется следующим образом
H(0) =

Отсюда получим
А(1)=(H(0))T*A(0)*H(0)=

Максимальный
по модулю наддиагональный элемент
равен ![]()
Определим угол поворота
![]()
![]()
![]()
Тогда матрица поворота H(1) определяется следующим образом
H(1) =

Отсюда получим
А(2)=(H(1))T*A(1)*H(1)=

Максимальный
по модулю наддиагональный элемент
равен ![]()
Определим угол поворота
![]()
![]()
![]()
Тогда матрица поворота H(2) определяется следующим образом
H(2) =

Отсюда получим
А(3)=

Максимальный
по модулю наддиагональный элемент
равен ![]()
Определим угол поворота
![]()
![]()
![]()
Тогда матрица поворота H(3) определяется следующим образом
H(3) =

Отсюда получим
А(4)=

Максимальный
по модулю наддиагональный элемент
равен ![]()
Определим угол поворота
![]()
![]()
![]()
Тогда матрица поворота H(4) определяется следующим образом
H(4) =

Отсюда получим
А(5)=

Максимальный
по модулю наддиагональный элемент
равен ![]()
Определим угол поворота
![]()
![]()
![]()
Тогда матрица поворота H(5) определяется следующим образом
H(5) =

Отсюда получим
А(6)=

Максимальный
по модулю элемент
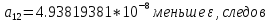 ательно,
для решения задачи потребовалось 6
итераций.
ательно,
для решения задачи потребовалось 6
итераций.
Собственные
числа: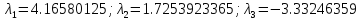 .
.
Найдем собственные векторы:
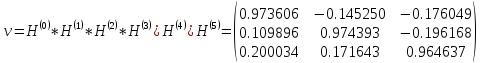 ;
;
Ответ: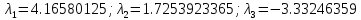 ;
;
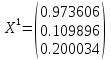 ;
;
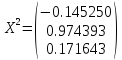 ;
;
Задание 5
Найти степенным методом с точностью ε=0,0001 максимальное по модулю собственное число λ1 матрицы А и соответствующий ему собственный вектор Х(1), так, чтобы ǁХ(1)ǁ2=1. Проверить, вычислив невязку АХ(1)-λ1Х(1). Найти противоположную к λ1 границу спектра собственных чисел.
Решение:
А=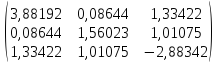
Выбираем начальное
приближение собственного вектора
Х1(0)=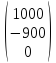 .
Найдем:
.
Найдем:
Х1(1)=А*
Х1(0)=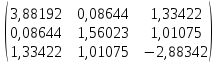
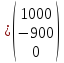 =
=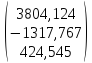 ;
;
λ1(1)=
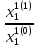 =
=
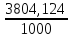 = 3,80412.
= 3,80412.
Вычислим:
Х1(2)=А*
Х1(1)=
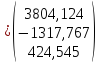 =
= ;
;
λ1(2)=
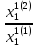 =
=
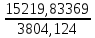 = 4,00088.
= 4,00088.
Так как │ λ1(2)- λ1(1) │= 0,1967533869 > ε , то процесс необходимо продолжить. Результаты вычислений представлены в таблице 1.
Таблица 1. Результаты вычислений
|
k |
x11(k) |
x21(k) |
x31(k) |
λ1(k) |
│ λ1(k)- λ1(k-1) │ |
|
0 |
1000,00000 |
-900,00000 |
0,00000 |
- |
- |
|
1 |
3804,12400 |
-1317,76700 |
424,54500 |
3,80412 |
- |
|
2 |
15219,83369 |
-1298,08227 |
2519,46378 |
4,00088 |
0,1967533869 |
|
3 |
62331,48953 |
1836,84355 |
11729,89759 |
4,09541 |
0,0945346134 |
|
4 |
257774,89655 |
20109,82634 |
51198,28828 |
4,13555 |
0,0401364759 |
|
5 |
1070709,60000 |
105406,68629 |
216628,26107 |
4,15366 |
0,0181127775 |
|
6 |
4454550,12288 |
475967,82685 |
910471,71015 |
4,16037 |
0,0067106369 |
|
7 |
18548119,43708 |
2047929,87615 |
3799162,00747 |
4,16386 |
0,0034872928 |
|
8 |
77248256,79729 |
8638544,07385 |
15862637,32207 |
4,16475 |
0,0008895427 |
|
9 |
321782516,74413 |
36188615,61119 |
66058931,89950 |
4,16556 |
0,0008147453 |
|
10 |
1340399279,45176 |
151046509,89983 |
275430667,30169 |
4,16554 |
0,0000193237 |
|
11 |
5583864336,13239 |
629922956,83201 |
1146875491,80034 |
4,16582 |
0,0002775009 |
|
12 |
23260749402,77740 |
2624698331,49048 |
4779874372,60558 |
4,16571 |
0,0001134576 |
|
13 |
96900651230,82160 |
10937050278,22860 |
19905485543,26930 |
4,16584 |
0,0001357185 |
|
14 |
403664271573,54200 |
45559875760,85230 |
82945535328,73270 |
4,16575 |
0,0000899497 |
Точность достигнута на 14 итерации. │ λ1(14)- λ1(13) │=0,0000899497 < ε .
λ max =4,16575;
Х*= .
.
По условию ǁх(1)ǁ2=1, следовательно, умножаем собственный вектор на 1,8791*10-12.
Х*= .
.
АХ(1)-λ1Х(1)
=
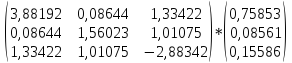 –
4,16575*
–
4,16575* =
=
=
 –
–
 =
=
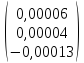 .
.
Так как λ1(А)>0, следовательно, требуется найти λ*=min λ2(A). λ2(B)≤ 0.
λ*– λ1(А)=max λ2(B);
B=
A
– λ1(А)*E= 4,16575*
4,16575*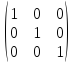 =
=
=

Х1(0)= .
Найдем:
.
Найдем:
Х1(1)=B*
Х1(0)= =
=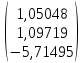 ;
;
λ1(1)=
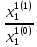 =
=
 =1,05048.
=1,05048.
Вычислим:
Х1(2)=А*
Х1(1)=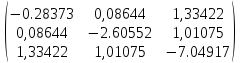
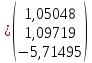 =
= ;
;
λ1(2)=
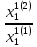 =
=
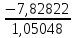 = -7,45197.
= -7,45197.
Так как │ λ1(2)- λ1(1) │= 8,5024552858 > ε , то процесс необходимо продолжить. Результаты вычислений представлены в таблице 2.
Таблица 2. Результаты вычислений
|
k |
x11(k) |
x21(k) |
x31(k) |
λ1(k) |
│ λ1(k)- λ1(k-1) │ |
|
0 |
1,00000 |
0,00000 |
1,00000 |
– |
– |
|
1 |
1,05049 |
1,09719 |
-5,71495 |
1,05049 |
– |
|
2 |
-7,82822 |
-8,54433 |
42,79622 |
-7,45197 |
8,5024552858 |
|
3 |
58,58210 |
64,84204 |
-320,75860 |
-7,48346 |
0,0314910096 |
|
4 |
-438,97909 |
-488,09015 |
2404,78241 |
-7,49340 |
0,0099428414 |
|
5 |
3290,86981 |
3664,41711 |
-18030,75183 |
-7,49664 |
0,0032444506 |
|
6 |
-24673,95598 |
-27487,83170 |
135196,38879 |
-7,49770 |
0,0010568325 |
|
7 |
185006,41921 |
206137,02848 |
-1013726,13941 |
-7,49804 |
0,0003440503 |
|
8 |
-1387207,07631 |
-1545725,89097 |
7601120,15635 |
-7,49816 |
0,0001119842 |
|
9 |
10401546,25275 |
11590341,74179 |
-56994770,04216 |
-7,49819 |
0,0000364473 |
λ1(9)=
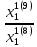 = -7,49819.
= -7,49819.
│ λ1(2)- λ1(1) │= 0,0000364473 < ε;
λ*= -7,49819+4,16575= -3,33244.
