Задание 7
Выписать
интерполяционный многочлен Ньютона
для узловых значений
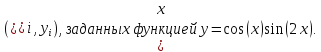 Н
Н .
.
Решение
Значения
функции в точках

|
i
|
0
|
1
|
2
|
3
|
4
|
5
|
|
xi
|
1.0
|
1.2
|
1.4
|
1.6
|
1.8
|
2
|
|
f(xi)
|
0.4913
|
0.2448
|
0.05694
|
0.0017
|
0.10054
|
0.315
|
Вычислим
коэффициенты из формулы:



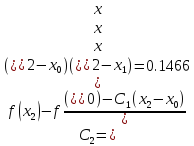



Построим
интерполяционный полином Ньютона по
формуле:



Вычислим
значение функции в точке


Значение
функции
 в этой же точке:
в этой же точке:


Ответ:


Задание 8
Вычислить
решение методом Рунге-Кутты-Мерсона с
точностью
 Построить график решения в Matlab.
Построить график решения в Matlab.



График
представлен на рисунке 1.

Рисунок 1. Графическое
решение методом Рунге-Кутты-Мерсона
Код
программы в Matlab:
Головная
программа
%
Решение задачи №8 (вычисление решения
методом Рунге-Кутты-Мерсона).
%--------------------------------------------------------------------------
clc;
clear;
%--------------------------------------------------------------------------
options
= odeset ('RelTol',
1e-5); %
Задание точности, равной 0.00001.
[T,Y] =
ode45(@RungeKuttyMersona,[0
10], [0.5], options); %
Решение методом ode45.
newplot
= plot(T,Y(:,1),'b'),
grid %
Построение графика решения.
set(newplot,
'LineWidth',
2); %
Установка жирной линии графика newplot.
%
Подписываем название графика, оси и
легенду:
title('Графическое
решение методом Рунге-Кутты-Мерсона.');
xlabel('Ось
X');
ylabel('Ось
Y''');
legend('y''
= -6y^2 + 1/x^2');
%--------------------------------------------------------------------------
Функция
function
dy = RungeKuttyMersona(x,y) %
Сигнатура
функции.
dx =
zeros(1,1); %
Формирование массива нулей 1x1.
k(1) =
-6; %
Задание
k(2) =
1; %
коэффициентов.
dy(1) =
k(1)*y^2+k(2)/x^2;
%--------------------------------------------------------------------------


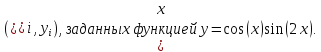 Н
Н .
.



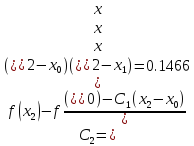








 в этой же точке:
в этой же точке:




 Построить график решения в Matlab.
Построить график решения в Matlab.


