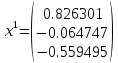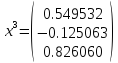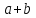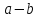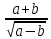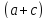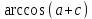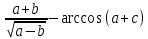Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Новосибирский государственный технический университет»
Кафедра экономической информатики
Расчетно-графическая работа
по дисциплине «Численные методы»
Вариант №28
Выполнила:
Группа: ФБИ-22
Руководитель: Соболева О.Н.
Новосибирск 2014
Задание 1
Запишите порядок выполняемых вами операций, оцените погрешности их результатов, вычислите и запишите искомое значение. Определите число верных знаков.
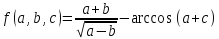
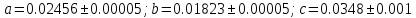
Абсолютные погрешности исходных данных:
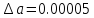
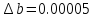
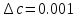
Порядок выполняемых операций:
Воспользуемся универсальными оценками для функции нескольких переменных:
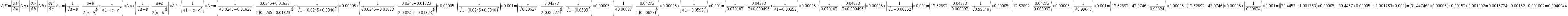
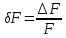
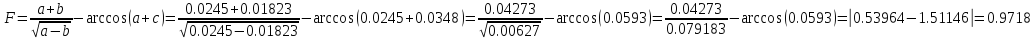
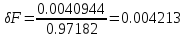
Так
как
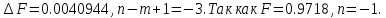
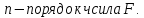
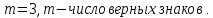
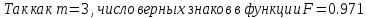
Задание 2
Выясните погрешность задания исходных данных, необходимую для получения результата с m мерными значащими цифрами.
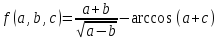
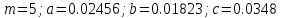
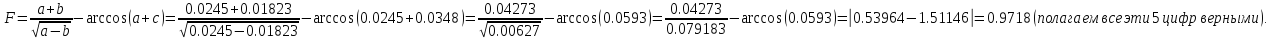
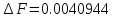
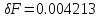
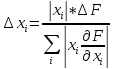
Находим
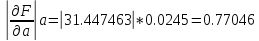
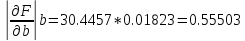
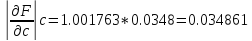
знаменатель
Отсюда допустимая погрешность исходных параметров равна:
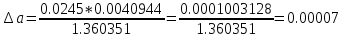
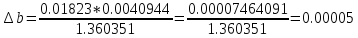
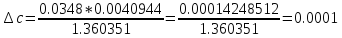
Задание 3
Решить СЛАУ методом Гаусса и, с точностью до = 0.001, методом простой итерации
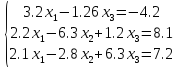
Решение методом Гаусса
Перепишем систему уравнений в матричном виде и решим его методом Гаусса.
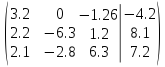
Первую строку делим на 3.2
От второй строки отнимаем первую строку, умноженную на 2.2 и
от третьей строки отнимаем первую строку, умноженную на 2.1
Вторую строку делим на -6.3
От третьей строки отнимаем вторую строку, умноженную на -2.8
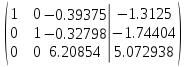
Третью строку делим на 6.20854
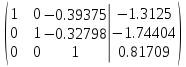
От первой строки отнимаем третью строку, умноженную на -0.39375 и
От второй строки отнимаем третью строку, умноженную на -0.32798
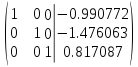
Решением системы
Проверка
Решение методом простой итерации с точностью до = 0.001
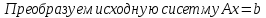
к виду
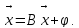
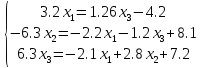
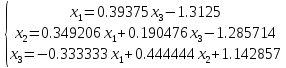
При этом норма
матрицы
,
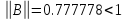достаточное условие сходимости
выполняется.
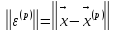
Шаг 1
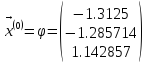
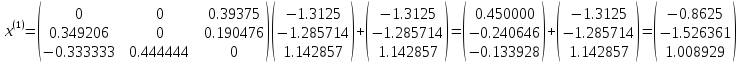
Шаг 2
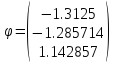
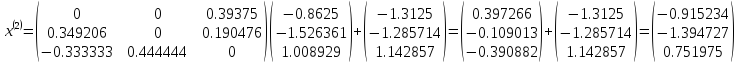
Шаг 3
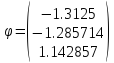
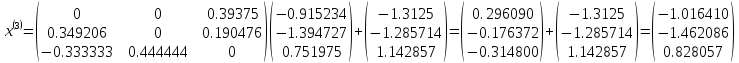
Шаг 4
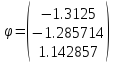
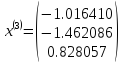
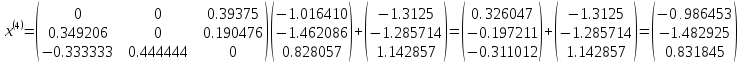
Шаг 5
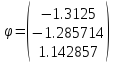
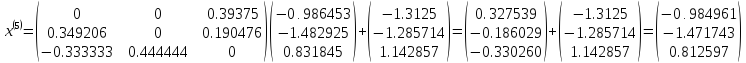
Шаг 6
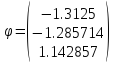
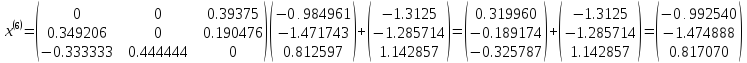
Шаг 7
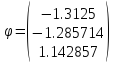
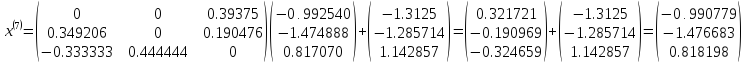
Шаг 8
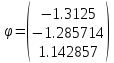
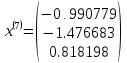
Шаг 9
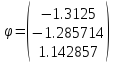
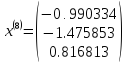
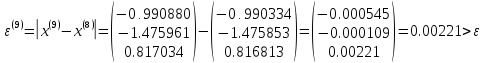
Шаг 10
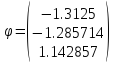
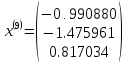
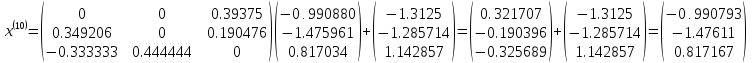
Решением системы
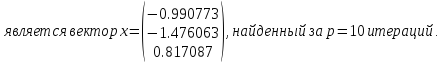
Проверка:
Задание 4
Методом вращения с точностью до = 0.00001 вычислить собственные значения и собственные векторы симметрической матрицы А.
Решение
Шаг 1
Выделим максимальный
по модулю наддиагональный элемент,
равен
,
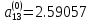так как
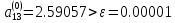
Определим угол поворота
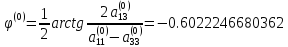
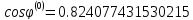
Сформируем
матрицу вращения
Выполним первую итерацию
Шаг 2
Выделим максимальный
по модулю наддиагональный элемент,
равен
,
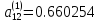так как
Определим угол поворота
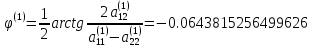
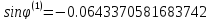
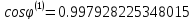
Сформируем
матрицу вращения
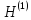
Выполним вторую итерацию
Шаг 3
Выделим максимальный
по модулю наддиагональный элемент,
равен
,
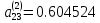так как
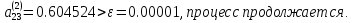
Определим угол поворота
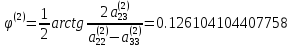
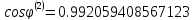
Сформируем
матрицу вращения
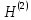
Выполним третью итерацию
Шаг 4
Выделим максимальный
по модулю наддиагональный элемент,
равен
,
так как
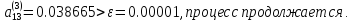
Определим угол поворота
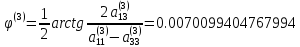
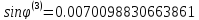
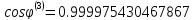
Сформируем
матрицу вращения
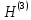
Выполним четвертую итерацию
Шаг 5
Выделим максимальный
по модулю наддиагональный элемент,
равен
,
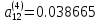так как
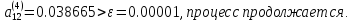
Определим угол поворота
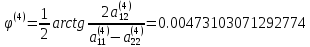
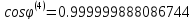
Сформируем
матрицу вращения
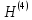
Выполним пятую итерацию
Шаг 6
Выделим максимальный
по модулю наддиагональный элемент,
равен
,
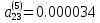так как
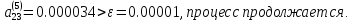
Определим угол поворота
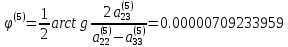
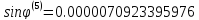
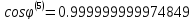
Сформируем
матрицу вращения
Выполним шестую итерацию
Так
как наддиагональные элементы = 0 и
,
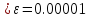следовательно, процесс прекращается и
для решения нам потребовалось 6 итераций.
Ответ:
Собственные значения матрицы A:
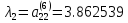
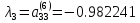
Собственные
векторы определяются как столбцы
матрицы
