Открытые оптические резонаторы

Во многих генераторах СВЧ в качестве колебательной систе­мы используются закрытые резонаторы в виде различной конфи­гурации отрезков волноводов. Причем для существования колеба­ний только одного типа или с небольшим количеством перемен знака поля в резонаторе (малое число мод) размеры последнего должны быть соизмеримы с длиной волны. Это условие для оп­тического диапазона неосуществимо. Поэтому в лазерах приме­няются открытые резонаторы, в которых используются две (или более) отражающие поверхности, между которыми происходит многократное отражение сферической или плоской волны, чем и обеспечивается взаимодействие волны с активным веществом.

Разновидности открытых резонаторов обусловлены формой от­ражающих поверхностей, в качестве которых используются зер­кала различной формы (плоские, сферические, параболические), грани призм полного внутреннего отражения, многослойные тон­костенные пластинки, границы раздела сред с различными пока­зателями преломления показаны на рис. 15, а: 1— активная сре­да; 2— плоские зеркала; 3 — сферические зеркала; 4 — призма.

Расстояние между зеркалами зависит от размеров активного вещества и в современных квантовых генераторах составляет де­сятые доли миллиметра в полупроводниковых лазерах и до де­сятков метров — в газовых. В последнем случае резонатор содер­жит несколько секций (рис. 15,б).

В случае криволинейных отражающих поверхностей зеркала должны быть конфокальными, т. е. их фокусы расположены в центре резонатора. Причем радиус кривизны зеркал R равен рас­стоянию между зеркалами L.

Теория и практика использования многослойных тонкостенных пластинок вместо зеркал с целью дополнительного разрешения спектра открытых резонаторов полностью не разработана.

Рассмотрим структуру поля в открытом резонаторе. Предпо­ложим вначале, что резонатор пассивный (активная среда отсут­ствует). Вдоль оси резонатора распространяется плоская волна

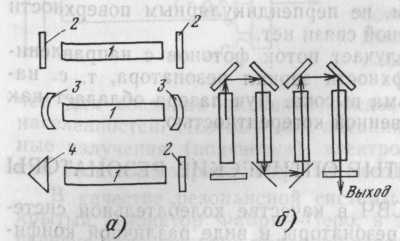
Рис. 15 Разновидности открытых резо­наторов

Рис. 16 К пояснению модовых режимов лазера

(или почти плоская), которая, интерферируя с отраженной от зеркала волной, создает q пучностей и узлов, количество которых зависит от соотношения длины волны  и длины резонатора L. Числом q определяется тип (мода) продольной структуры волны, обычно q= 10⁵...10⁷.

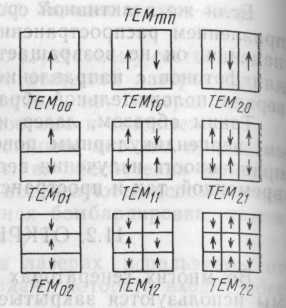
Поперечная структура волны аналогично типам волн в волно­воде определяется количеством перемен знака вектора поля в плоскости, перпендикулярной оси резонатора. Число т — количе­ство перемен знака по оси х, а n — по оси у. Таким образом, при­нято обозначение типа волны TEM_mnq. Для поперечных мод часто индекс q опускается. Волна с индексами т= п = 0

Рис. 17 Сечения луча лазера для разных мод

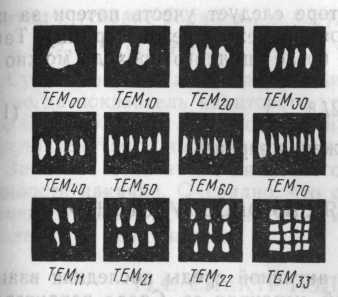
является основ­ной (рис. 16) и обозначается TEM_OOq или ТЕМ₀₀ — это одномо-довый режим. Следует отметить, что чем выше порядок, тем боль­ше поперечное сечение луча. Это легко обнаружить при визуальном наблюдении луча, падающего на плоскую поверхность. На рис. 17 приведены сечения луча для разных мод.

Остановимся на потерях мощности в резонаторе. Если предпо­ложить, что зеркала представляют собой абсолютно гладкие отражающие поверхности неограниченных размеров, то плоская волна, многократно отражаясь от зеркал, могла бы существовать вечно, т. е. имела бы место ситуация, аналогичная существованию незатухающих колебаний в контуре без потерь. В реальном резо­наторе существуют потери, обусловленные следующими факто­рами.

Любая поверхность не может обладать стопроцентной отражающей способностью по множеству причин (рассеивание, погло­щение и др.), т. е. коэффициент отражения г > 1. Кроме того, одно из зеркал полупрозрачно

Рис. 18. Зависимость ди­фракционных потерь от числа Френеля и моды

и часть энергии уходит на излучение.

Другим фактором является дифракция волны. Если на зерка­ло падает плоская волна, то из-за дифракции на краях отражен­ная волна распространяется в пределах некоторого малого угла:

/D (57)

где D — диаметр зеркала.

Вследствие дифракции часть энергии теряется при каждом отражении. Дифракционные потери определяются показателем потерь _дифр, который обратно пропорционален числу Френеля:

N  D²/L. (58)

Дифракционные потери растут с увеличением поперечных ин­дексов моды. На рис. 18 приведены зависимости _дифр от числа Френеля и моды. Сплошными линиями показаны зависимости для резонаторов с конфокальными зеркалами, а штриховыми — с плос­кими зеркалами. Для снижения потерь стремятся понизить порядок поперечной моды. При малых значениях индексов т и п энергия поля сосредоточена вблизи оси резонатора и падает до нуля на краях зеркала.

Потери возрастают с уменьшением числа Френеля, т. е. с ростом длины резонатора L либо при уменьшении диаметра зерка­ла D. В конфокальных резонаторах потерь меньше. Это позволяет при той же выходной мощности использовать меньший объем активного вещества. Помимо всего, в конфокальных резонаторах менее жесткие требования к юстировке зеркал, нежели в резонаторе с плоскими зеркалами. Однако направленность излучения в конфокальных резонаторах хуже.

Для оценки поля в резонаторе следует учесть потери за пол­ный проход волны (два расстояния между резонаторами). Таким образом, для амплитуды поля после полного прохода можно за­писать

Е_т (2L) = Е_т (0) r₁ r₂ ехр (- 2Lβ_дифр), (59)

где r₁ r₂ — коэффициенты отражения зеркал.