Возможность усиления и генерации в квантовых приборах

Определим условия, при которых в квантовых приборах воз­можны усиление либо генерация. Для этого исследуем поведение двухуровневой квантовой системы с энергетическими уровнями W₂>W₁ и населенностями в исходном состоянии N₂<N₁ (на верх­нем уровне W₂ меньше частиц, чем на нижнем). Облучим эту си­стему электромагнитным полем, подлежащим усилению, на час­тоте перехода: v₂₁= (W₂-W₁)/ ћ. Выясним, при каких условиях об­лучающее поле будет усиливаться за счет энергии, стимулированно излученной частицами. Обозначим текущие значения населенностей нижнего и верхнего уровней N*₁ и N*₂ и с помощью (28) и (29) найдем результирующую мощность Р, которой об­менивается облучающее поле с квантовой системой:

Р=(BρN*₂ - BρN*₁)ћν₂₁ =Bρ(N*₂ -N*₁)ћν_21. (30)

Из (30) видно, что знак мощности Р зависит от соотношения между населенностями верхнего и нижнего уровней. В частности, для положительных значений Р, т.е. для усиления облучающего поля, необходимо и достаточно выполнение условия

n*₂>n*₁ (31)

Таким образом, усиление и генерация в квантовых приборах прин­ципиально возможны в том, и только в том случае, когда текущее значение населенности верхнего уровня больше, чем нижнего.

Состояние квантовой системы, при котором населенность верх­него уровня больше населенности нижнего, называется состояни­ем с инверсной населенностью, а среда с инверсной населенностью называется инверсной или активной.

Что же касается возможного равенства населенностей верхне­го и нижнего уровней (n*₂= n*₁), то из (30) видно, что в этом случае Р = 0, т.е. сигнал в среде не усиливается и не ослабляется. Среда для сигнала является прозрачной. Такое состояние с рав­ными населенностями уровней называют насыщением перехода.

Только активная среда обеспечивает увеличение мощности об­лучающего поля.

Структурная схема квантового усилителя показана на рис. 4. Принцип его действия сводится к тому, что входным сигналом, подлежащим усилению, облучаются частицы активной среды. Ес­ли частота сигнала совпадает с частотой квантового перехода, то частицы верхнего уровня стимулированно излучают энергию и уве­личивают мощность входного сигнала. Поэтому

Pвых = Рвх + Pа, (32)

где Р_а — результирующая мощность, излученная активной средой. Из (32) видно, что мощность выходного сигнала Pвых возраста­ет по сравнению с Рвх на Pа.

Рассмотрим закон изменения мощности усиливаемого сигнала вдоль направления распространения волны. Через единичное сечение активной среды (рис. 5,а) распространяется плоская волна. При прохождении через среду поток энергии S изменяется. Изменение dS в слое dz за 1с равно

dS = Pdz, (33)

где мощность определяется по (30).

Рис. 4. Структурная схема квантового усилителя

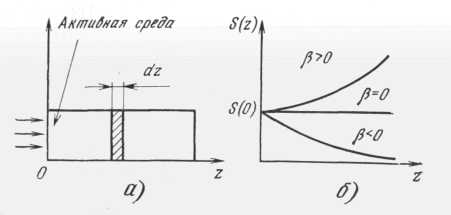
Рис. 5. К выводу закона Бугера

С другой стороны, поток энергии равен произведению объемной плотности энергии ρ на групповую скорость v_гp:

S = ρ v_гp (34)

Подставляя (30) в (33), с учетом (34) получаем

dS/S = (Bρ(N*₂ -N*₁)ћν₂₁/v_гp) dz (35)

или

dS/S =  dz, (36)

где

(37)

Выражение (36) в оптике называется дифференциальным зако­ном Бугера, а коэффициент β —коэффициентом поглощения. Интегрируя (9.36) в пределах от 0 до z, получаем интегральный за­кон Бугера:

S(z) = S(0)exp(z). (38)

В пассивной среде коэффициент поглощения отрицателен, так как N₂<N₁. Следовательно, S(z) будет убывать вдоль z. При N₂=Ni среда абсолютно прозрачна, а при N₂>N₁ будет наблюдать­ся усиление.

Согласно (38) поток энергии при β>0 должен неограничен­но возрастать по экспоненте (рис. 5,б). Здесь не учтены два обстоятельства: наличие потерь α на стенках и неоднородностях среды и зависимость β от объемной плотности энергии ρ, которая, в свою очередь, зависит от z.

Таким образом, в общем, виде дифференциальный закон Бугера можно записать в виде

dS (z)/dz=- S (z) [() - ]. (39)

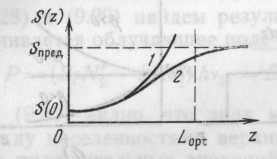
Рис. 6. К пояснению влияния дли­ны активной среды

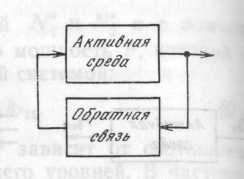
Рис. 7. Структурная схема генера­тора

Из анализа (39) можно сделать полезные выводы. Из (37) видно, что при малых уровнях  (в начале оси z) разность N₂^* - N₁^* велика и () » . Нарастание S вдоль оси z идет по экспоненци­альному закону. Далее S и  (34) возрастают, что приводит к увеличению вынужденных излучений, а значит, к уменьшению разности N₂^* - N₁^* Согласно (37) () при этом будет умень­шаться, стремясь к . Темп нарастания потока энергии S(z) замедляется.

Выражение (39) представляет собой производную зависимо­сти S(z) от z. Очевидно, что при достижении () =  производная становится равной нулю, т. е. рост S{z) прекращается из-за насыщения перехода (N₂^* = N₁^*).

На рис. 6 показаны зависимости S(z): кривая 1 при условии, что  = const, и кривая 2 с учетом убывания N₂^* - N₁^* вдоль оси z. Видно, что S(z) стремится к некоторому пределу S_пред. Отсюда можно сделать важный вывод, что удлинение пути волны ( длины активной среды L) не приводит к существенному эффекту. При заданных уровнях входной мощности S(0) существует некоторая оптимальная длина, которая учитывается при проектировании прибора.

Для построения генератора необходимо выход усилителя соединить с входом элементом обратной связи (рис. 7).

Если в усилителе поле, облучающее активную среду, возбуждается входным сигналом, подлежащим усилению, то в квантовом генераторе такое поле первоначально возникает в результате флуктуаций, и в частности из-за спонтанного излучения.

Для создания активной среды в современных квантовых приборах используются два основных метода: сортировка частиц по энергетическим состояниям и создание инверсии населенностей.