Ширина спектральной линии

Применительно к двухуровневой системе (3) можно предста­вить в виде

v₂₁= (W₂-W₁)/ ћ. (13)

откуда вытекает, что при строго фиксированных W₂ и W₁ излуча­ется энергия на одной-единственной частоте, т. е. излучение монохроматично. Однако в реальных системах уровни W₂ и W₁ не яв­ляются бесконечно тонкими. В силу ряда причин они имеют конеч­ную ширину, или «размытость». Кроме того, с повышением темпе­ратуры размытость энергетического уровня увеличивается. Поэто­му частота v₂₁ не является строго фиксированной, и поглощение энергии квантовой системой либо излучение наблюдается в неко­торой полосе частот ∆v. Эта полоса тем уже, чем больше время жизни частиц на верхнем уровне.

Из теории колебаний известно, что если длительности сигнала ∆t соответствует полоса частот ∆v, то

∆t ∆v ≈1, (14)

Из (3) можно установить, что какому-либо изменению энергии ∆W частицы сопутствует изменение частоты перехода

∆v = ∆W/h. (15)

Подставляя (15) в (14), получаем

∆W∆t ≈ h (16)

Выражение (16) является одним из соотношений неопределен­ностей Гейзенберга, сформулированных им в 1927 г.

Поскольку постоянная Планка h есть числовой коэффициент, то из (16) видно, что некоторой размытости уровня ∆W соответствует неопределенность момента времени ∆t перехода частицы с одного уровня на другой. Поскольку спонтанные переходы имеют статистический характер, то неопределенность ∆t выражается в произвольности времени жизни τ₂ частицы на верхнем уровне, т. е. ∆t= τ. Тогда (16) можно представить в виде

∆W τ ≈ h. (17)

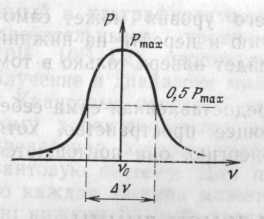
Рис. 3. Спектральная линия излучения

Монохроматическому излучению соот­ветствует равенство ∆v = 0, которое выполнимо лишь при ∆W=0. Но для этого, как следует из (17), требует­ся, чтобы τ → ∞, т.е. время жизни частиц на верхнем уровне должно быть неограниченным. Поскольку это невозможно, размытость уровня ∆W является конечной величиной и, следовательно, излучение не является монохроматичным.

Таким образом, частицы излучают целый спектр частот, обра­зующий спектральную линию (рис. 3).

Из рис. 3 видно, что максимум мощности Рmax излучается (поглощается) на средней частоте перехода v₀. Однако из-за раз­мытости уровней имеется излучение (поглощение) и на других частотах. Ширина спектральной линии ∆v отсчитывается на уров­не половинной мощности 0,5Рmax.

Если частицы не подвержены внешним воздействиям, то ∆v, определяемая по (15) и (16), обусловлена только временем жизни частиц τ на верхнем уровне. Такое значение ∆v называется естественной шириной спектральной линии, которая фактически обусловлена только спонтанным излучением.

Естественная ширина спектральной линии с ростом частоты существенно увеличивается. Так, для молекулы аммиака с часто­той перехода 23870 МГц спектральная линия имеет естественную ширину порядка 10^-3 Гц, а для рубина с частотой перехода 4.10¹⁴ Гц естественная ширина спектральной линии составляет 10¹¹ Гц.

Форма спектральной линии при естественной ее ширине может быть представлена так называемой лоренцевой кривой, совпадаю­щей с резонансной характеристикой колебательного контура.

В реальных условиях наблюдается «уширение» спектральных линий, т. е. они становятся шире естественных. Если при уширении форма спектральной линии остается лоренцевой, а меняется лишь ее ширина, то такое уширение называется однородным. Различают так­же неоднородное уширение, при котором изменяется форма спект­ральной линии. Основные причины уширения спектральной линии: соударения молекул между собой и со стенками резонатора, эффект Доплера, влияния электрических и магнитных полей, эффект насыщения. В кристаллах, кроме того, наблюдается уширение спектральной линии из-за колебаний кристаллической решетки.

В газообразном веществе частицы из-за хаотического теплово­го движения непрерывно сталкиваются между собой и со стенка­ми сосуда (резонатора). При этом может измениться энергетиче­ское состояние частицы. Следовательно, может уменьшиться вре­мя релаксации τ, а это в соответствии с (17) и (15) приводит к увеличению ширины спектральной линии ∆ν.

При больших давлениях газа, когда число частиц в единице объема велико, уширение определяется в основном столкновения­ми частиц, а при малых давлениях (разреженный газ) основную роль в уширении играют столкновения частиц со стенками резо­натора. Например, для аммиака при давлении 40 Па уширение достигает 10⁷ Гц, а в разреженном газе из-за соударений со стен­ками сосуда ширина спектральной линии 3.10⁴ Гц.

Для борьбы с описанным видом уширения используют разре­женный газ, остро направленные пучки молекул, проходящие ре­зонатор «навылет». Кроме того, стенки резонатора покрывают спе­циальными пленками, чтобы при соударении не изменялось энер­гетическое состояние молекул.

Причиной уширения спектральной линии является также эф­фект Доплера: частота излучения частиц газа, воспринимаемая приемником энергии, зависит от скорости и направления их дви­жения (доплеровское уширение). При хаотичности движения ши­рина спектральной линии увеличивается. Например, для молекул аммиака при комнатной температуре доплеровское уширение составляет 70 кГц.

Основной метод борьбы с доплеровским уширением — исполь­зование атомных и молекулярных пучков, пролетающих в направ­лении, перпендикулярном направлению приема излучения. При этом уширение снижается до 2...3 кГц.

Что же касается влияния электрических полей, то в них из-за эффекта Штарка энергетические уровни смещаются. То же самое происходит в магнитных полях (эффект Зеемана). При этом из-за появляющейся размытости уровней происходит уширение спект­ральной линии.