32

Московский энергетический институт (Технический университет) Кафедра «Электронные приборы»

В.Н. Бодров, Г.И. Обидин

Физические основы квантовых приборов

учебное пособие

к расчетному заданию по курсу

"Квантовые и оптоэлектронные приборы и устройства ".

(учебный план 2003г, индекс СД07)

Москва, 2005г.

АННОТАЦИЯ

В учебном пособии излагаются физические основы оптических квантовых генераторов электромагнитного излучения видимого и ИК - диапазонов длин волн, рассматриваются общие вопросы квантовой электроники, такие как энергетические уровни системы частиц, разрешенные квантовые переходы, факторы, определяющие ширину спектральной линии, вопросы взаимодействия квантовых систем с электромагнитным излучением, возможность усиления и генерации излучения в квантовых приборах, способы создания инверсии населенностей, принцип действия и структурная схема лазера, открытые оптические резонаторы, условия самовозбуждения и спектр излучения лазера. На примере гелий-неонового лазера рассмотрено устройство, конструктивные особенности и основные характеристики оптических квантовых генераторов.

СОДЕРЖАНИЕ

Энергетические уровни системы частиц………………………………………….4

Квантовые переходы……………………………………………………………….6

Ширина спектральной линии……………………………………………………...8

Взаимодействие квантовых систем с электромагнитным излучением………10

Возможность усиления и генерации в квантовых приборах………………….12

Способы создания инверсии населённостей……………………………………15

КВАНТОВЫЕ ГЕНЕРАТОРЫ ОПТИЧЕСКОГО ДИАПАЗОНА……………..20

Структурная схема лазера………………………………………………………...20

Открытые оптические резонаторы……………………………………………….22

Условия самовозбуждения лазера…………………………………………….....25

Спектр излучения лазера……………………………………………………........26

Газовые лазеры…………………………………………………………………….28

Вопросы для самоконтроля………………………………………………………30

Список литературы…………………………………………………………………..31

Энергетические уровни системы частиц

В квантовых приборах для усиления и генерации электромагнитного излучения используется внутренняя энергия таких частиц, как атомы, молекулы и ионы. Отсюда вытекает основная особенность физических свойств квантовых приборов в сравнении с электронными.

В электронных приборах, как известно, используется движение свободных электронов в вакууме, газе либо твердом теле. При этом движущийся свободный электрон может быть уподоблен бегущей волне. Если электрон движется со скоростью v, то его длина волны по формуле де Бройля

λ=ћ/mv, (1)

где m - масса электрона; ћ =6,63.10^-34 Дж с =4,14.10^-15 эВ с — постоянная Планка. Поскольку скорость свободного электрона может быть произвольной, то произвольными являются длина волны и энергия электрона.

В квантовых же приборах используется движение связанных электронов. Движущийся связанный электрон можно уподобить стоячей волне. При этом длина волны не может быть произвольной: Для нее допустимы лишь некоторые дискретные значения. Следовательно, скорость связанного электрона, а значит, и его энергия могут принимать только ряд дискретных значений, т. е. кван­туются.

Возможные значения энергии частицы называются уровнями энергии (энергетическими уровнями), совокупность которых является энергетическим спект­ром частицы.

Если энергия атома, молекулы либо иона изменяется от W_к до W_i, то говорят, что частица совершила переход с уровня W_к на уровень W_i. При W_к >W_i наблюдается излучение кванта

ћ_ki= (W_к-W_i) (2)

где v_ki — частота, на которой излучается квант, или частота энергетического пе­рехода.

Из третьего постулата Бора (2) следует, что частота перехода определяется только энергетическим расстоянием W_к >W_i, т. е.

_ki= (W_к-W_i)/ ћ. (3)

Графически уровни энергии можно изобразить по аналогии с потенциальной энергией тела, поднятого на различные высоты (уровни), где каждому зна­чению энергии W, отложенному по вертикали, соответствует горизонтальная прямая (рис. 1).

Самый нижний уровень, соответствующий наименьшей возможной энергии, называется основным, а все остальные являются возбужденными, так как для перехода на них с основного уровня частица должна возбудиться — поглотить определенную энергию. В дальнейшем совокупность частиц будем называть квантовой системой.

Согласно принципу Паули в квантовой системе не может быть более двух электронов с одинаковыми энергиями. Поэтому энергетический уровень одно­именных взаимодействующих между собой частиц расщепляется на множество различных уровней. Для того чтобы одноименные уровни каждой частицы в системе были одинаковыми, частицы не должны взаимодействовать между со­бой, т. е. их следует разнести на определенные расстояния друг от друга. Только такие системы будем рассматривать в дальнейшем.

Уровни энергии одноэлектронных атомов в основном определяются средней удаленностью электрона от ядра, которая характеризуется главным квантовым числом n=1, 2, 3,...:

W_n =-R/n²+W_∞, (4)

где R — постоянная; W_∞ —энергия ионизации атома.

Энергетические уровни, описываемые (4), не являются одиночными. Они расщепляются на ряд подуровней. Это объясняется тем, что каждому значению главного квантового числа соответствует свой орбитальный момент количества движения, обусловленный движением электрона вокруг ядра. Этот момент опре­деляется орбитальным квантовым числом l

l = n - 1. (5)

Кроме того, электрон, вращаясь вокруг собственной оси, обладает еще спино­вым моментом количества движения (спином). Полный момент количества движения j атома равен сумме орбитального и спинового моментов и определяется квантовым числом полного момента количества движения:

j = l+ s, (6)

где s — спиновое квантовое число.

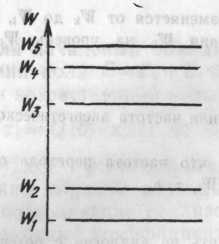
Рис. 1. Уровни энер­гии частиц при слабом взаимодействии между атомами

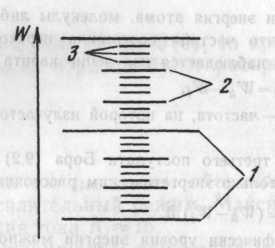
Рис. 2. Электронные, ко­лебательные и вращатель­ные энергетические уровни в молекуле

В многоэлектронном атоме орбитальные моменты отдельных электронов складываются в суммарный орбитальный момент, а спиновые моменты — в сум­марный спиновый, суммируются также соответствующие квантовые числа:

(7)

Квантовое число полного момента количества движения атома определяется по формуле

j = L+S. (8)

Что же касается многоатомной молекулы, то ее энергетический спектр гораздо сложнее атома. Но в первом приближении полную внутреннюю энергию молекулы можно представить суммой трех слагаемых:

W=W_эл+W_кол+W_вр, (9)

где W_эл — электронная энергия, обусловленная движением электронов; W_кол — колебательная энергия, обусловленная колебательным движением атомов друг относительно друга; W_вр — вращательная энергия, которая определяется вращательным движением молекулы как целого.

В соответствии со структурой (9) в энергетическом спектре молекулы различают уровни: 1 — электронные; 2—колебательные; 3 — вращательные (рис. 2).