
- •§ 1. Линейные пространства. Базисы
- •Определение линейного пространства
- •7) При любом и любых ;
- •Решение. Докажем, что для множества с введенными операциями не выполнено свойство 7) линейного пространства, т.Е. .
- •Линейная зависимость векторов
- •Базис. Размерность линейного пространства Определение 5. Всякую систему векторов линейного пространства X называют базисом, или базой, этого пространства, если:
- •Рассмотренные в примерах базисы называются стандартными. Если – базис в линейном пространстве X, то любые n линейно независимых векторов также образуют базис в X.
- •Иначе – находим произвольный вектор , для которого не существует такое, что выполняется равенство (*), то есть:
- •Упражнения к § 1
- •§ 2. Линейные подпространства. Прямая сумма подпространств. Произведение пространств
- •Если n – четное, то в пространстве число таких векторов ; если n – нечетное, то . Объединив эти два случая, получим, что число векторов .
- •Упражнения к § 2
- •§ 3. Определители и линейная независимость векторов
- •Упражнения к § 3
- •§ 4. Линейные нормированные пространства
- •§ 5. Пространства со скалярным произведением. Евклидовы пространства
- •Упражнения к § 5
- •Литература
Упражнения к § 2
Доказать, что все n-мерные векторы, у которых первая и последняя координаты равны между собой, образуют линейное подпространство. Найти его базис и размерность.
Доказать, что все n-мерные векторы, у которых координаты с четными номерами равны между собой, образуют линейное подпространство. Найти его базис и размерность.
Доказать, что все симметрические матрицы образуют линейное подпространство пространства всех квадратных матриц порядка n. Найти его размерность и базис.
Доказать, что линейное пространство есть прямая сумма двух линейных подпространств:
 ,
,
 .
.
Доказать, что пространство всех квадратных матриц есть прямая сумма пространств симметрических матриц и кососимметрических матриц.
Доказать, что решения любой системы однородных линейных уравнений с n неизвестными ранга r образуют линейное подпространство n- мерного пространства размерности n-r.
§ 3. Определители и линейная независимость векторов
Пусть
X
– конечномерное линейное пространство
и
![]() – система векторов из X.
– система векторов из X.
Определение
1. Векторы
![]() ,
,
![]() называются базисными
для системы векторов
,
если они линейно независимы и каждый
из векторов
является их линейной комбинацией.
называются базисными
для системы векторов
,
если они линейно независимы и каждый
из векторов
является их линейной комбинацией.
Число
базисных векторов называется рангом
системы векторов
.
Базисные векторы образуют базис в
линейной оболочке векторов
,
т.е. в подпространстве
![]() .
.
Для
того чтобы векторы
![]() (
(![]() )
образовывали базис в
,
необходимо и достаточно, чтобы определитель
матрицы
)
образовывали базис в
,
необходимо и достаточно, чтобы определитель
матрицы
![]() был отличен от нуля.
был отличен от нуля.
Столбцы
матрицы A,
на которых расположен базисный минор
матрицы A,
являются базисными векторами для системы
векторов
![]() .
.
Задача
1. Найти базисные
векторы в системе векторов
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Решение.
Составим
матрицу из координат векторов
![]() .
.
Найдем какой-либо базисный минор матрицы A.
Рассмотрим
![]() ;
;
 .
.
Следовательно,
rang(A)=3.
Так как базисный минор расположен на
векторах
![]() ,
то данные векторы являются базисными
векторами системы
,
то данные векторы являются базисными
векторами системы
![]() .
.
Упражнения к § 3
1. Найти размерность и базис линейных подпространств, натянутых на следующие системы векторов:
=(1, 0, 0, -1), =(2, 1, 1, 0), =(1, 1, 1, 1),
 =(1,
2, 3, 4),
=(1,
2, 3, 4),
![]() =(0,
1, 2, 3);
=(0,
1, 2, 3);
=(1, 2, 3), =(4, 5, 6), =(7, 8, 9), = (10, 11, 12).
§ 4. Линейные нормированные пространства
Определение
1. Линейное
пространство над полем K
(K=R
или K=C)
называется
нормированным,
если задана функция
![]() ,
обозначаемая
,
обозначаемая
![]() и удовлетворяющая следующим условиям:
и удовлетворяющая следующим условиям:
 ,
,
 ;
; ;
; ;
;
для любых векторов и любого числа .
Величина
![]() называется нормой вектора x.
называется нормой вектора x.
Задача 1. Доказать, что линейное пространство , где K=R или K=C является нормированным, если в качестве нормы выбрана одна из следующих функций:
 (октаэдрическая
норма);
(октаэдрическая
норма); (кубическая
норма)
(кубическая
норма) (евклидова
норма),
(евклидова
норма),
где
![]() .
.
Решение.
Докажем, что для
 выполняются аксиомы нормы.
выполняются аксиомы нормы.
Так как
 для любого
для любого
 ,
то
,
то
 .Условие
.Условие
 равносильно
равносильно
 ,
а так как
,
то равенство нулю суммы возможно лишь
тогда и только тогда, когда
,
а так как
,
то равенство нулю суммы возможно лишь
тогда и только тогда, когда
 ,
,
 ,
т.е.
,
т.е.
 .
. .
. ,
а так как по свойству модуля
,
а так как по свойству модуля
 ,
то
,
то
 .
.
Таким образом, является нормой в .
II.
Докажем, что
![]() является нормой в
.
является нормой в
.
Так как , то
 .
Условие
.
Условие
 равносильно
равносильно

 ,
а так как, с другой стороны,
,
а так как, с другой стороны,
 ,
то получаем:
,
то получаем:
 .
. .
.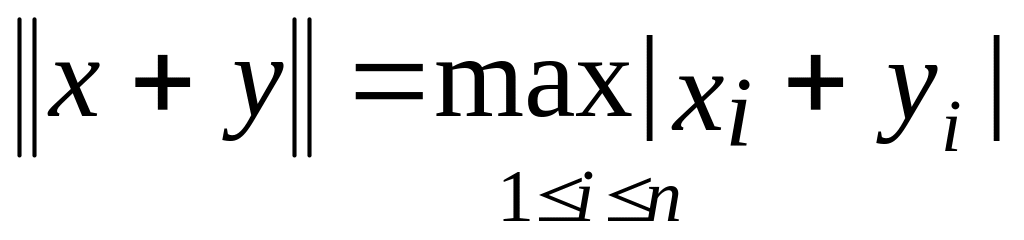 .
Так как
,
то
.
Так как
,
то
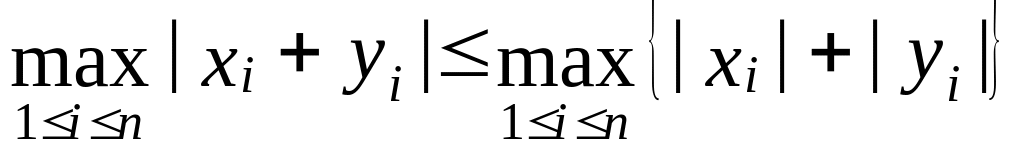 .
Так как
.
Так как
 , то
, то
 .
Аналогично,
.
Аналогично,
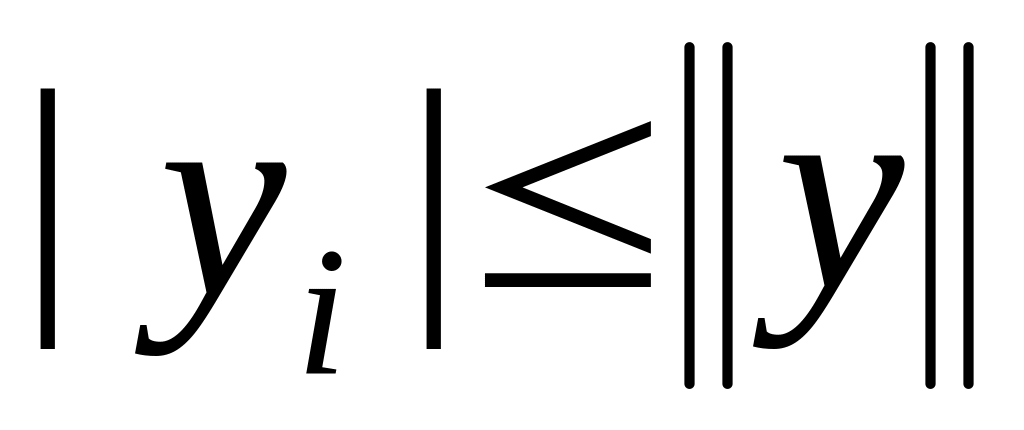 ,
,
 .
Следовательно,
.
Следовательно,
 .
.
Таким образом, является нормой в .
Аналогично
проверяется (доказательство проведите
самостоятельно), что
![]() является
также нормой в пространстве
.
является
также нормой в пространстве
.
Задача
2.Докажите
неравенство
![]() .
.
Решение.
1)
![]() ,
следовательно,
,
следовательно,
![]() ;
;
2)
![]() ,
следовательно,
,
следовательно,
![]() ,
а так как
,
а так как
![]() ,
то последнее неравенство преобразуется
к виду:
,
то последнее неравенство преобразуется
к виду:
![]() .
.
Из пунктов 1) и 2) следует, что .
