
- •§ 1. Линейные пространства. Базисы
- •Определение линейного пространства
- •7) При любом и любых ;
- •Решение. Докажем, что для множества с введенными операциями не выполнено свойство 7) линейного пространства, т.Е. .
- •Линейная зависимость векторов
- •Базис. Размерность линейного пространства Определение 5. Всякую систему векторов линейного пространства X называют базисом, или базой, этого пространства, если:
- •Рассмотренные в примерах базисы называются стандартными. Если – базис в линейном пространстве X, то любые n линейно независимых векторов также образуют базис в X.
- •Иначе – находим произвольный вектор , для которого не существует такое, что выполняется равенство (*), то есть:
- •Упражнения к § 1
- •§ 2. Линейные подпространства. Прямая сумма подпространств. Произведение пространств
- •Если n – четное, то в пространстве число таких векторов ; если n – нечетное, то . Объединив эти два случая, получим, что число векторов .
- •Упражнения к § 2
- •§ 3. Определители и линейная независимость векторов
- •Упражнения к § 3
- •§ 4. Линейные нормированные пространства
- •§ 5. Пространства со скалярным произведением. Евклидовы пространства
- •Упражнения к § 5
- •Литература
Иначе – находим произвольный вектор , для которого не существует такое, что выполняется равенство (*), то есть:
![]() ,
,
![]() .
.
Полагаем
![]() .
Отметим, что векторы
.
Отметим, что векторы
![]() – линейно независимы в силу нарушения
(*).
– линейно независимы в силу нарушения
(*).
Если для любого вектора существуют
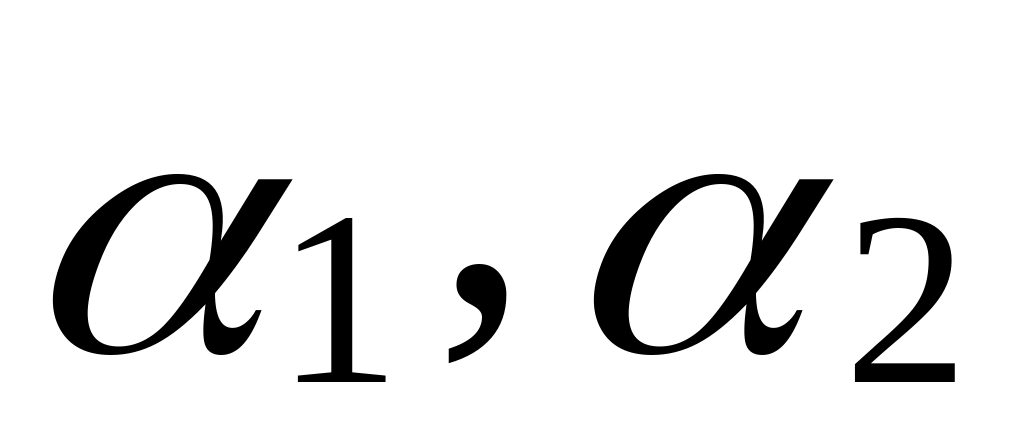
 такие, что:
такие, что:
![]() ,
(**)
,
(**)
то останов, dim X=2; – базис в X.
Иначе
– находим вектор
![]() ,
для которого не выполнено равенство
(**):
,
для которого не выполнено равенство
(**):
![]() ,
,
![]() .
.
Полагаем
![]() ;
– линейно независимые векторы.
;
– линейно независимые векторы.
Продолжая данный процесс для конечномерного линейного пространства, через конечное число шагов алгоритма будет найден базис в пространстве X.
Задача
12. Систему
многочленов
![]() ,
,
![]() ,
,
![]() ,
,
![]() дополните до базиса пространства
дополните до базиса пространства
![]() .
.
Решение.
Так
как размерность пространства многочленов
степени не выше 5 :
равна 6, то необходимо найти многочлены
![]() ,
являющиеся линейно независимыми как
между собой, так и с многочленами
,
являющиеся линейно независимыми как
между собой, так и с многочленами
![]() .
.
Найдем
произвольный многочлен
![]() ,
являющийся линейно независимым с
системой
.
Очевидно, что в качестве такого многочлена
можно выбрать
,
являющийся линейно независимым с
системой
.
Очевидно, что в качестве такого многочлена
можно выбрать
![]() .
.
Для
нахождения последнего многочлена базиса
воспользуемся алгоритмом 1, т.е. найдем
многочлен
,
являющийся линейно независимым с
системой
![]() ,
т.е. для которого не существуют числа
,
т.е. для которого не существуют числа
![]() такие, что выполняется равенство:
такие, что выполняется равенство:
![]()
![]()
![]()
![]()
![]()
Неизвестными
системы являются
;
![]() - параметры системы. Система не имеет
решения, например, для следующих значений
параметров:
- параметры системы. Система не имеет
решения, например, для следующих значений
параметров:
![]() .
Тогда в качестве базисного многочлена
выберем
.
Тогда в качестве базисного многочлена
выберем
![]() .
.
Система
многочленов
![]() линейно независима и образует базис в
пространстве
.
линейно независима и образует базис в
пространстве
.
Упражнения к § 1
Доказать, что множество всех функций со значениями в данном поле K, определенные на множестве из n элементов, составляют n-мерное векторное пространство над полем K по отношению к действиям сложения функций и умножения на константу поля K.
В множестве
 положительных действительных чисел
определены операции:
положительных действительных чисел
определены операции:
«сложения»
 ;
;«умножения на действительное число»
 .
.
Проверить, что множество с указанными операциями образует линейное пространство.
Будет ли множество всех многочленов
 ,
удовлетворяющих следующим условиям,
линейным пространством относительно
обычных операций сложения и умножения
на число:
,
удовлетворяющих следующим условиям,
линейным пространством относительно
обычных операций сложения и умножения
на число:
f(0)=1; f(1)=0;
2f(0)-3f(1)=0.
Пусть
 – множество всех упорядоченных пар
действительных чисел
– множество всех упорядоченных пар
действительных чисел
 с операциями:
с операциями:
 ;
; .
.
Будет ли действительным линейным пространством?
Доказать, что система векторов, содержащая нулевой вектор, линейно зависима.
Выяснить, являются ли следующие системы векторов арифметических пространств линейно зависимыми:
 (-3,
1, 5);
(-3,
1, 5);
 =
(6, -2, 15);
=
(6, -2, 15);(1, 2, 3); =(2, 5, 7);
 =(3,
7, 11);
=(3,
7, 11); =(2,
-3, 1);
=(3,
-1, 5);
=(1,
-4, 3).
=(2,
-3, 1);
=(3,
-1, 5);
=(1,
-4, 3).
Найти все значения параметра , при которых вектор b линейно выражается через векторы

 ,
,
 :
:
 =(3,
4, 2);
=(3,
4, 2);
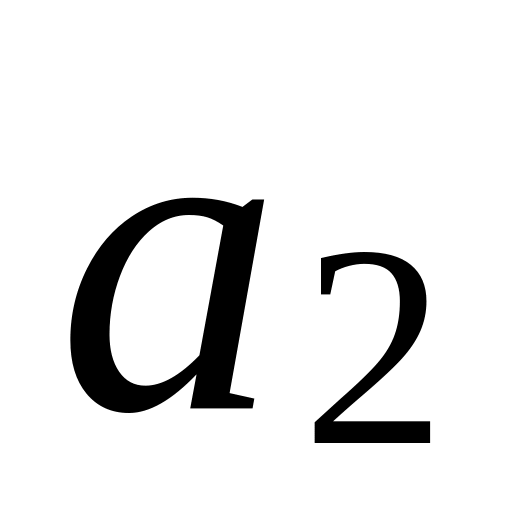 =(6,
7, 8);
b=(9,
12, );
=(6,
7, 8);
b=(9,
12, );=(3, 2, 5); =(2, 4, 7); =(5, 7, ); b=(1, 3, 5).
Являются ли многочлены
 линейно независимыми:
линейно независимыми:
 ,
,
 ,
,
 ?
?
Векторы и x заданы своими координатами в некотором базисе. Показать, что сами образуют базис и найти координаты вектора x в этом базисе:
=(2, 1, -3),
 =(3,
2, -5),
=(3,
2, -5),
 =(1,
-1, 1), x=(6,
2, -7);
=(1,
-1, 1), x=(6,
2, -7);= (1, 2, -1, -2); =(2, 3, 0, -1); =(1, 2, 1, 4);
![]() =(1,
3, -1, 0); x=(7,
14, -1, 2);
=(1,
3, -1, 0); x=(7,
14, -1, 2);
=(2, 2, -1), =(2, -1, 2), =(-1, 2, 2), x=(1, 1, 1);
4) =(1, 5, 3), =(2, 7, 3), =(3, 9, 4), x=(2, 1, 1).
Систему векторов =(1, 2, -1); =(2, 1, 0) дополните до базиса в пространстве .
Показать, что следующие системы векторов являются базисами пространства
 :
:
= (1, 2, 3, …, n); = (0, 2, 3, …, n); = (0, 0, 3, …, n); …;
![]() =(0,
0, 0, …, n);
=(0,
0, 0, …, n);
= (1, 1, …, 1, 1, 1); =(1, 1, …, 1, 1, 0);
=(1, 1, …, 1, 0, 0); =(1, 0, …, 0, 0, 0).
Проверить, какая из следующих систем векторов является базисом пространства
 :
:
=(1, 2, -1, -2), =(2, 3, 0, -1), =(1, 2, 1, 3),
![]() =(1,
3, -1, 0);
=(1,
3, -1, 0);
=(1, 2, -1, -2), =(2, 3, 0, -1), =(1, 2, 1, 4),
=(1, 3, -1, 0).
Найти координаты многочлена
 в каждом из следующих базисов пространства
в каждом из следующих базисов пространства
 :
:
1, t+1,
 ,
,
 ,
,
 ,
,
 ;
; ,
,
 ,
,
 ,
,
 ,
,
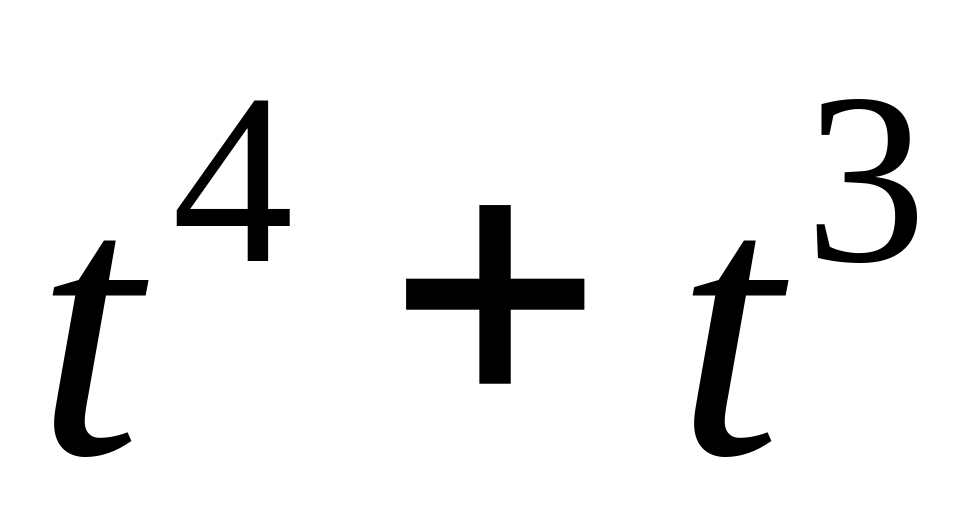 ,
,
 .
.
