9.3. Методы устранения автокорреляции

1.Обобщенный МНК (ОМНК)

Рассмотрим исходную модель в моменты времени t и t–1:

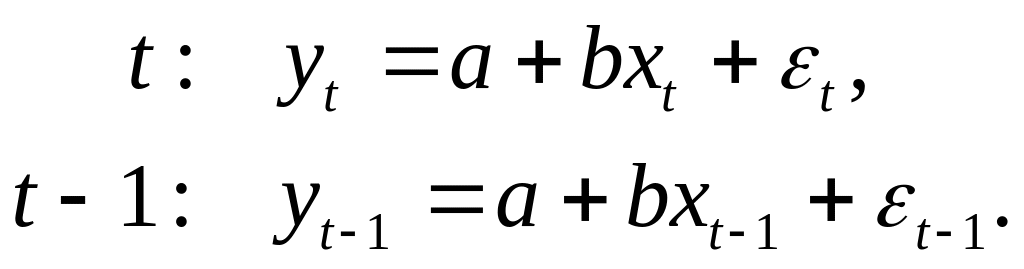
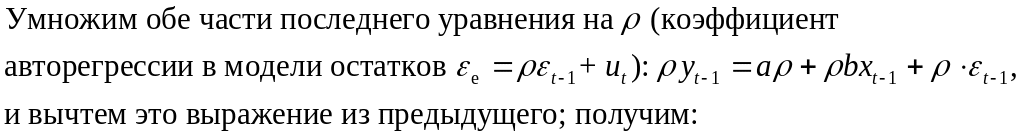
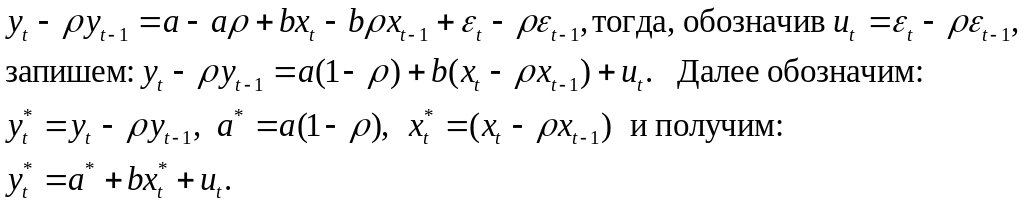
– есть случайная величина, так как и – случайные величины,

, так как и .

Остаток не коррелирует ни с одним регрессором, следовательно, можно применить классический МНК. Оценка параметра b вычисляется непосредственно, а оценка параметра a вычисляется так: .

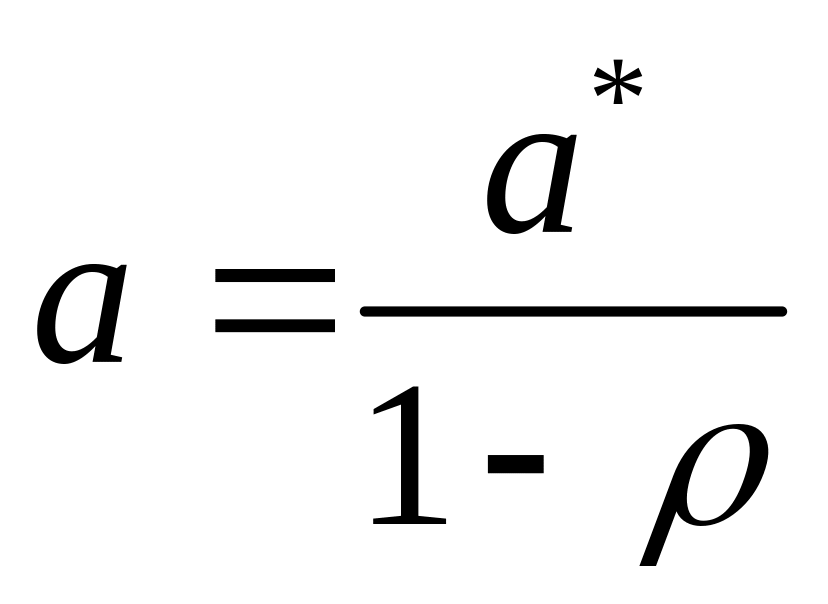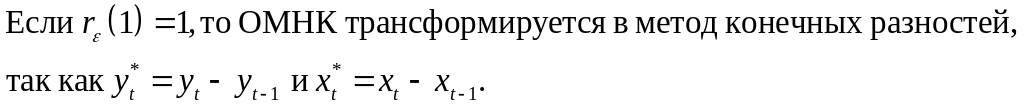
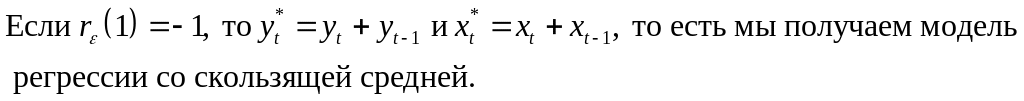
ОМНК может применяться для данных, начиная с момента , т.е. первое наблюдение теряется; его можно восстановить для и , используя поправку Прайса–Уинстена:

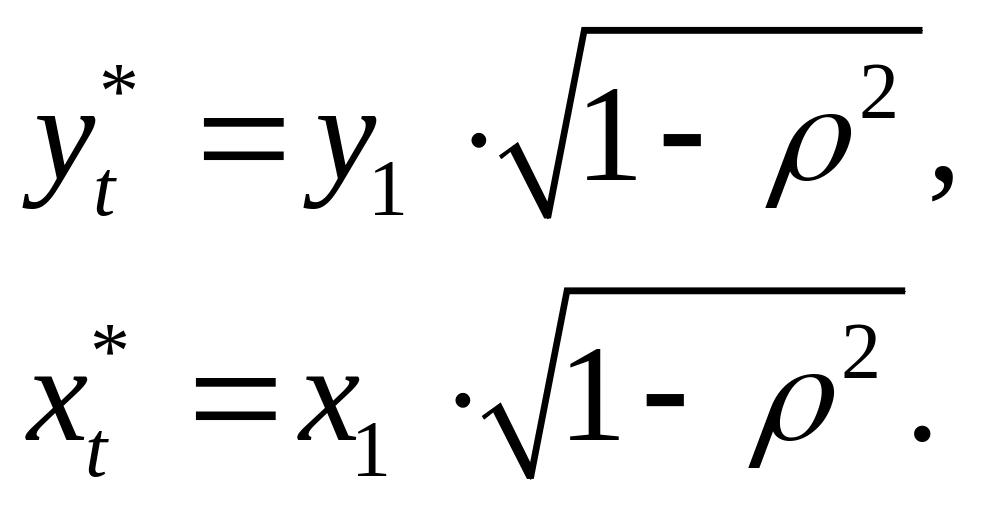
Если наше предположение о том, что остатки описанные – моделью первого порядка соответствуют действительности, то можно показать, что .

При большой протяженности временного ряда значения и действительно оказываются близки друг к другу. В матричной форме отыскание столбца B с помощью ОМНК выражается так:

B = (X^TΩ_ρX)^-1X^TΩ_ρY, где

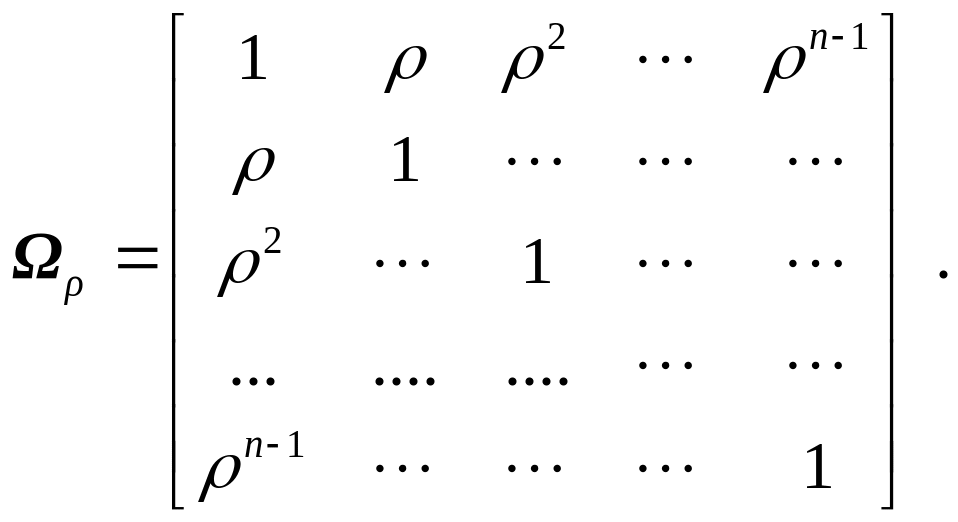
2. Метод Кохрана – Оркатта (итерационный)

Первая итерация: вначале по МНК оценивается регрессия . Определяются столбец остатков и столбец . Далее оценивается авторегрессия остатков по схеме :

, отсюда находится оценка .

Вторая итерация: Введем новые переменные: w_t = y_t – ρy_t-1, z_t = x_t – ρx_t-1.

Построим регрессию По ней определим (ε₁)_t и (ε₁)_t-1. Далее опять построим авторегрессию остатков , отсюда находим оценку ρ₁.

Третья итерация: Опять введем новые переменные (w₁)_t = w_t – ρ₁w_t–1,

(z₁)_t = z_t – ρ₁z_t–1 и построим регрессию По ней определим

остатки (ε₂)_t и (ε₂)_t-1. Построим авторегрессию остатков и по ней найдем оценку ρ₂.

Итерационный процесс продолжается до тех пор, пока разность между предыдущей и последующей оценками ρ не станет по модулю меньше любого наперед заданного числа. После того, как определено значение ρ, строится регрессия по уже знакомой модели:

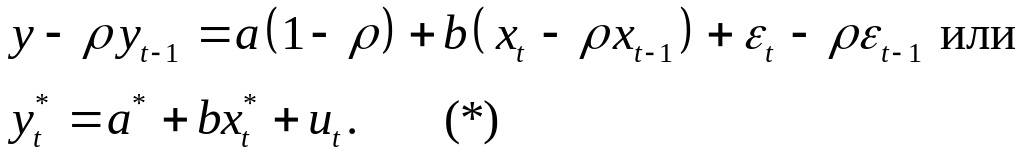
Применяя к этому уравнению классический МНК находим и , рассчитываем значение

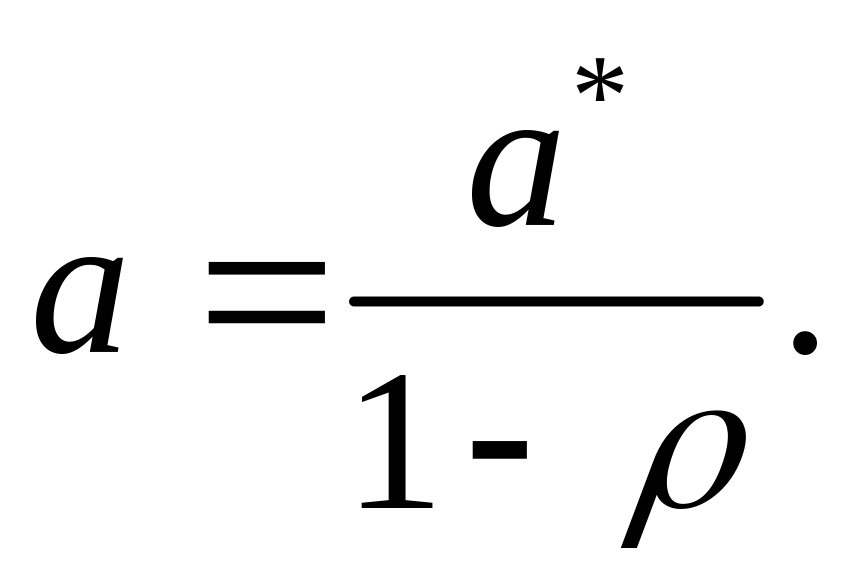
3. Метод Хилдрета-Лу

Этот метод предполагает перебор значений с достаточно малым шагом, например, 0,01 и подстановку его в уравнение (*). Та величина , при которой стандартная ошибка регрессии в данной модели будет наименьшей, принимается в качестве наилучшей оценки

10. Системы одновременных уравнений

10.1. Виды переменных и уравнений соу

В экономических, социальных и финансовых науках объекты статистических исследований достаточно сложны. Каждое отдельное взятое уравнение множественной регрессии не может характеризовать истинные взаимосвязи между переменными модели системы.

Отсюда возникает необходимость создания СОУ (системы одновременных уравнений); ее особенность такова, что в одних уравнениях некоторая переменная рассматривается, как объясняющая, а в другое уравнение входит как объясняемая, т.е. зависимая переменная.

Примеры СОУ:

1. Модель спроса – предложения ( см. рис. 10.1):

P

S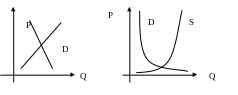

рис. 10.1

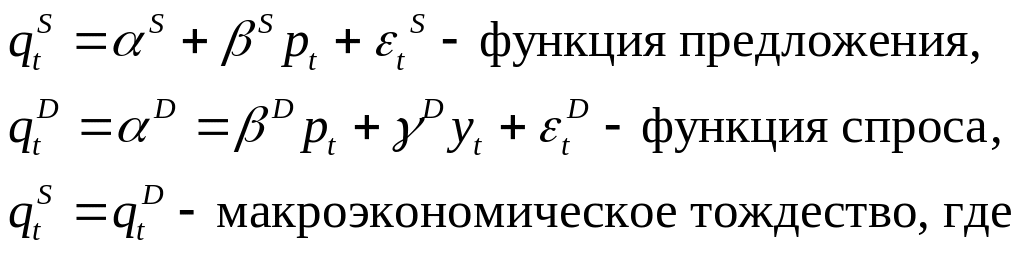
– предложение, - потребление, - доход.

2. Кейнсианская модель – модель формирования дохода (закрытая экономика без государственных расходов):

- потребление, - инвестиции, - доход.

Переменные делят на 2 больших класса:

– экзогенные – переменные внешние по отношению к модели (объясняющие или факторные переменные),

– эндогенные – переменные, значения которых определяются внутри модели.

Экзогенные всегда предопределенны, то есть определены заранее, до рассмотрения уравнения. К предопределенным переменным также относят лаговые значения эндогенных переменных. Уравнения, описывающие модель рассмотренным выше образом, называются структурными уравнениями и тогда имеет смысл говорить о структурной форме модели (СФМ). Уравнения подразделяются на:

– поведенческие (функциональные),

– уравнения – тождества.

Первые из них описывают взаимодействие между переменными и содержат случайные составляющие, а также параметры, подлежащие оцениванию. Уравнения – тождества этого не содержат и выполняются в любом случае. Можно создать систему независимых уравнений, в которой каждая эндогенная переменная будут выражена только через экзогенные и предопределенные переменные плюс случайная составляющая. Такие уравнения называются уравнениями в приведенной форме, и говорят, что системы таких уравнений имеют приведенную форму (ПФМ).

СФМ (неполная): ПФМ (полная):

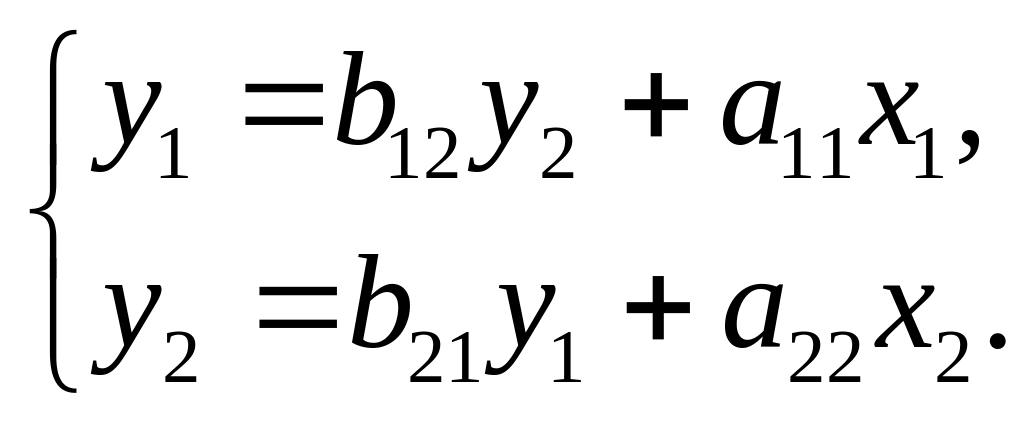
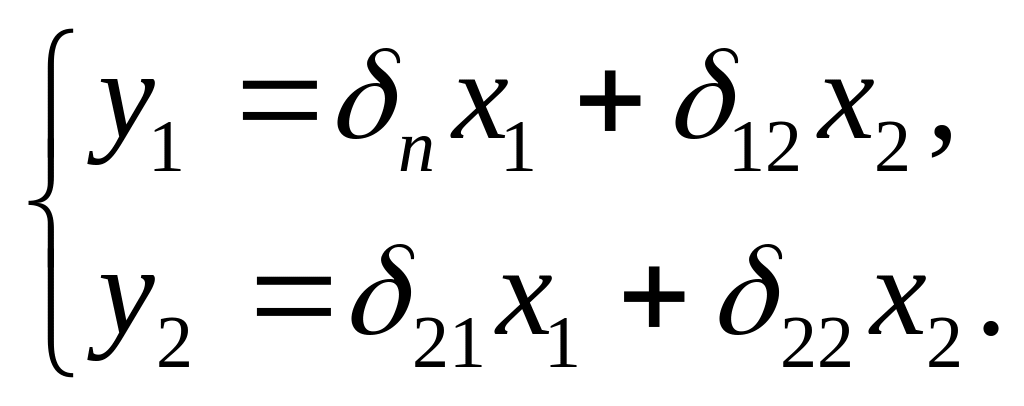
Структурную и приведенную формы, описываемые данными уравнениями, можно представить в виде графовой модели, как показано на рис.10.2. Видно, что СФМ представляет собой систему с перекрестными связями, а ПФМ – линейную систему с параллельными каналами.

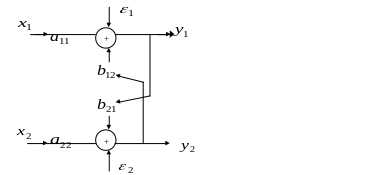
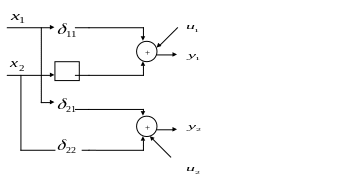
Рис. 10.2

В записанных выше системах для простоты случайные составляющие не включены, а все переменные взяты центрированными, чтобы в уравнении не было свободных членов. Напомним, что центрирование – это вычитание из истинного значения переменной ее среднего значения.

Для оценки параметров ПФМ можно использовать классический МНК, так как все уравнения независимы и для них выполняются условия Гаусса – Маркова.

К уравнениям СФМ применять непосредственно классический МНК нельзя, так как объясняющие переменные коррелируют со случайными составляющими. В связи с этим оценки могут получаться несостоятельными и смещенными. Следовательно, нужно использовать специальные методы методы оценки.