
Тема 6. Схема бернулли. Предельные теоремы в схеме бернулли
Если производятся испытания, при которых вероятность появления некоторого события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми относительно события А. Наступление события А при испытании часто называют “успехом”, в противном случае говорят о “неудаче”. Вероятности этих исходов обозначают p и q = 1 – p (0 p, q 1) соответственно. Если независимые испытания проводятся в одних и тех же условиях, то вероятность “успеха” в каждом испытании одна и та же. Описанная выше последовательность независимых испытаний с двумя исходами (“успехом” и “неудачей”) и постоянной вероятностью “успеха” в каждом испытании называется схемой Бернулли.
В схеме Бернулли основной интерес представляет вероятность Pn(k) того, что в n независимых испытаниях будет ровно k “успехов”. Если вероятность “успеха” в каждом испытании равна р, то вероятность Pn(k) определяется формулой Бернулли:
![]() (k
= 0, 1, …, n;
q = 1 –
p),
(6.1)
(k
= 0, 1, …, n;
q = 1 –
p),
(6.1)
где
– Число сочетаний из n по k.
Из формулы Бернулли (6.1) вытекает формула для вероятности Pn(k1; k2) того, что в n испытаниях событие А наступит не менее не менее k1, но не более k2 раз (от k1 до k2 раз):
Pn(k1;
k2)
=
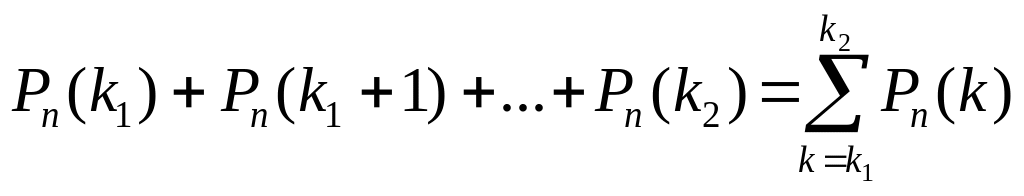 .
(6.2)
.
(6.2)
В качестве частного случая последней формулы получается следующая формула для вероятности того, что в n испытаниях событие А наступит хотя бы один раз:
![]() ,
(6.3)
,
(6.3)
где q = 1 – p.
При большом числе испытаний n вычисление вероятностей Pn(k) и Pn(k1, k2) по точным формулам (6.1) и (6.2) становится затруднительным. Поэтому возникает задача замены точных формул приближенными, снижающими вычислительные трудности без значительной потери точности вычислений. Предельные теоремы в схеме Бернулли дают такие формулы для приближенного вычисления вероятностей Pn(k) и Pn(k1, k2).
Локальная теорема Муавра – Лапласа. Если число испытаний n в схеме Бернулли достаточно велико, а вероятность “успеха” p не близка ни к 0, ни к 1, так что npq 9, то
Pn(k)
![]() ,
(6.4)
,
(6.4)
где
![]() и
и
![]() .
.
При решении задач, требующих применения локальной теоремы Муавра-Лапласа, пользуются специальными таблицами значений функции (х). Значения этой функции при х[0; 4] приведены в различных таблицах (см., например, в таблицу 1 Приложения 2 в [1] или таблицу 1.1 в [2]). Для отрицательных значений аргумента x пользуются теми же таблицами, поскольку функция (х) четная, т.е. ( –х) = (х). С увеличением значений аргумента x функция (х) 0 , так что при x 4 практически значения функции (х) 0.
Интегральная теорема Муавра – Лапласа. Если число испытаний n в схеме Бернулли достаточно велико, а вероятность “успеха” p не близка ни к 0, ни к 1, так что npq 9, то
Pn(k1; k2) Ф0(x2) – Ф0(x1), (6.5)
где
