
- •Тема 1. Геометрические векторы
- •1.1. Основные определения
- •1.2. Линейные операции
- •1.3. Координаты вектора
- •Примеры решения типовых задач Линейные операции над векторами
- •Разложение векторов
- •Тема 2. Векторные пространства
- •2.1. Линейные (векторные) пространства
- •2.2. Координатное -мерное пространство
- •2.3. Линейная зависимость векторов
- •2.4. Базис, координаты, размерность
- •2.5. Подпространства, линейные оболочки
- •Примеры решения типовых задач Линейная зависимость и независимость векторов
- •Базис, координаты
- •Тема 3. Линейные формы
- •3.1. Сопряженное пространство
- •3.2. Задание подпространств с помощью линейных форм
- •3.3. Матричная запись линейных форм
- •Примеры решения типовых задач Сопряженное пространство
- •Задание подпространств с помощью линейных форм
- •Тема 4. Линейные операторы
- •4.1. Определение линейного оператора
- •4.2. Матрица линейного оператора
- •4.3. Алгебра линейных операторов
- •Примеры решения типовых задач Линейные операторы
- •Операторы в геометрических пространствах
- •Операторы в функциональных пространствах
- •Матричная запись действия оператора
- •Тема 5. Определители
- •5.1. Определители второго и третьего порядков
- •5.2. Основные свойства определителя
- •5.3. Методы вычисления определителей
- •Тема 6. Алгебра матриц
- •6.1. Операции над матрицами
- •6.2. Обратная матрица
- •6.3. Матричные уравнения
- •Примеры решения типовых задач Операции над матрицами
- •Обратная матрица
- •Матричные уравнения
Тема 1. Геометрические векторы
1.1. Основные определения
Геометрическим
вектором
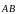 называется направленный отрезок прямой,
соединяющий точку
называется направленный отрезок прямой,
соединяющий точку
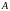 с точкой
с точкой
 .
Векторы принято обозначать также жирными
буквами
.
Векторы принято обозначать также жирными
буквами
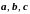 или буквами с чертой (стрелкой) сверху
или буквами с чертой (стрелкой) сверху
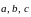 .
.
Длина
(модуль) вектора
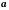 обозначается
обозначается
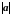 ,
длина вектора
,
длина вектора
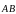 обозначается
обозначается
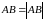 .
Векторы
.
Векторы
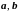 называются коллинеарными,
если они лежат на одной или на параллельных
прямых (обозначается
называются коллинеарными,
если они лежат на одной или на параллельных
прямых (обозначается
 ).
Коллинеарные векторы могут быть
сонаправлены (обозначается
).
Коллинеарные векторы могут быть
сонаправлены (обозначается
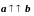 )
или противоположно направлены (
)
или противоположно направлены (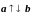 ).
Два вектора равны, если они коллинеарные,
сонаправлены и имеют одинаковую длину.
Это определение означает, что параллельное
перемещение не меняет вектора. Такие
векторы называются свободными.
).
Два вектора равны, если они коллинеарные,
сонаправлены и имеют одинаковую длину.
Это определение означает, что параллельное
перемещение не меняет вектора. Такие
векторы называются свободными.
1.2. Линейные операции
Суммой
 векторов
векторов
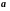 и
и
 называется вектор
называется вектор
 ,
соединяющий начало вектора
,
соединяющий начало вектора
 с концом вектора
с концом вектора
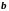 ,
при условии, что начало вектора
совпадает с концом вектора
.
Так, если
,
при условии, что начало вектора
совпадает с концом вектора
.
Так, если
 ,
то
,
то
 ,
так как
,
так как
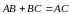 .
.
Произведением
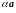 вектора
на число
вектора
на число
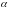 ,
называется вектор
,
коллинеарный вектору
,
длина которого
,
называется вектор
,
коллинеарный вектору
,
длина которого
 ,
сонаправленный вектору
,
если
,
сонаправленный вектору
,
если
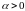 и противоположно направленный если
и противоположно направленный если
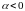 .
.
Операции сложения векторов и умножения вектора на число называются линейными.
Линейные операции обладают следующими свойствами:
L1.
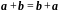 ; L2.
; L2.
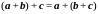 ;
;
L3.
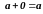 ;
L4.
;
L4.
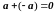 ;
;
L5.
 ; L6.
; L6.
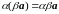 ;
;
L7.
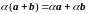 ;
L8.
;
L8.
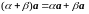 .
.
Эти свойства называются аксиомами линейного пространства.
1.3. Координаты вектора
Обозначим
символами
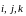 единичные векторы, лежащие на координатных
осях декартовой прямоугольной системы
координат. Для любого вектора
имеет место разложение
единичные векторы, лежащие на координатных
осях декартовой прямоугольной системы
координат. Для любого вектора
имеет место разложение
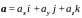 ,
где коэффициенты
,
где коэффициенты
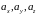 называются координатами вектора. Вектор,
таким образом, однозначно задается
своими координатами. Принято также
обозначение
называются координатами вектора. Вектор,
таким образом, однозначно задается
своими координатами. Принято также
обозначение
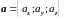 .
.
Векторы равны тогда и только тогда, когда равны их координаты.
Координаты векторов обладают свойством линейности, т.е. при сложении векторов их координаты складываются, а при умножении вектора на число его координаты умножаются на это число. Таким образом, линейные операции над векторами можно заменить линейными операциями над координатами.
Отсюда, в частности, следует, что координаты коллинеарных векторов пропорциональны.
Примеры решения типовых задач Линейные операции над векторами
Задача
1. Для
неколлинеарных векторов
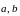 построить вектор
построить вектор
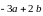
Р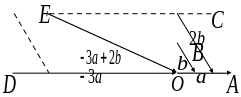 ешение.
Пусть
ешение.
Пусть
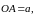 (см.рис.).
(см.рис.).
Вектор
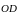 лежит на той же прямой, что и вектор
лежит на той же прямой, что и вектор
 ,
втрое длиннее вектора
и направлен в сторону, противоположную
вектору
.
Следовательно
,
втрое длиннее вектора
и направлен в сторону, противоположную
вектору
.
Следовательно
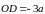 .
Вектор
.
Вектор
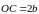 ,
а вектор
,
а вектор
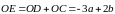 .
.
Задача
2. Даны векторы
 .
Найти вектор
.
.
Найти вектор
.
Решение.
Применив свойства линейных операций
над векторами, получим:
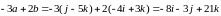 .
.
Задача
3. Даны векторы
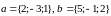 .
Найти вектор
.
.
Найти вектор
.
Решение.
При сложении векторов, заданных
координатами, их координаты складываются,
а при умножении вектора на число все
его координаты умножаются на это число.
Следовательно
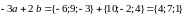 .
.
Задача
4. При каких
значениях
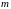 и
и
 векторы
векторы
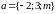 и
и
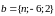 коллинеарны.
коллинеарны.
Решение.
Векторы, заданные координатами,
коллинеарны, если их координаты
пропорциональны, то есть
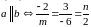 .
Получаем:
.
Получаем:
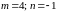 .
.
Задача
5. Найти
медиану
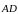 треугольника с вершинами в точках
треугольника с вершинами в точках
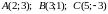 .
.
Решение.
Координаты точки
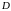 (середины отрезка
(середины отрезка
 )
равны полусумме координат точек
и
)
равны полусумме координат точек
и
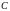 ,
то есть
,
то есть
 .
Координаты вектора
равны разности координат точек
и
,
то есть
.
Координаты вектора
равны разности координат точек
и
,
то есть
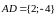 .
.
