3. Методика преподавания практических занятий

3.1. Перечень задач

1. Найти кислородный баланс тротила, гексогена, тэна, октогена.

2. Найти углеродный баланс тротила, гексогена, тэна, октогена.

3. Найти кислородный баланс алюминия и железа.

4. Найти кислородный баланс смеси тротила и гексогена в массовом соотношении 1:1.

5. Найти массовое соотношение смеси алюминия и перманганата калия, имеющей нулевой кислородный баланс.

6. Найти массовое и объемное отношение смеси метана и воздуха, имеющей нулевой кислородный баланс.

7. Найти массовое соотношение компонентов аммонита, состоящего из тротила и селитры и имеющего нулевой кислородный баланс. Ответ дать в процентах.

8. Ведется синтез детонационных алмазов в установке объемом 2 м³, заполненной смесью нейтрального газа аргон и воздух, из заряда ТГ50/50 (массовое отношение тротила и гексогена 1:1) массой 1 кг. Установлен выход конденсированного продукта 0,08 кг. Определить процентное содержание воздуха в смеси.

9. Ведется синтез детонационных алмазов во взрывной камере. Используется заряд ТГ 60/40 массой 0,5 кг. Получено 0,03 кг конденсированного продукта, содержащего 40 %. Определить процентный выход конденсированного продукта и алмазов от теоретически возможного

10. Найти мощность тротила плотностью 1,6·10³ кг/м³ и сравнить ее с мощностью Красноярской ГЭС.

11. Оценить, во сколько раз энергия, запасенная в 1 м³ тротила, больше электрической энергии конденсатора такого же объема.

12. Давление в детонационной зоне тротила составляет около 180·10³ атм. Что произойдет с тротилом, если его сжать статическим прессом до такого давления?

13. Конденсированный продукт детонационного синтеза имеет удельную поверхность около 400 м²/г. Какой объем кислорода, находящегося при н. у., может адсорбировать 1 кг порошка?

14. Оценить температуру во взрывной камере объемом 2 м³, заполненной воздухом при атмосферном давлении, после взрыва 500 г тротила, гексогена.

15. Оценить температуру во взрывной камере объемом 2 м³, заполненной воздухом при атмосферном давлении, после взрыва 500 г тротила, гексогена при условии, что заряд окружен водяной оболочкой объемом 2 л и вода после взрыва превращается в пар.

16. Оценить время остывания продуктов взрыва во взрывной камере после детонации 500 г тротила, гексогена.

17. Сколько надо времени для испарения 1 кг железа и алюминия в печи мощностью 5 кВт?

18. По проводу, сопротивление которого R = 6 Ом, протекло количество электричества q = 30 Кл. Определить количество теплоты, выделившееся в проводе в следующих случаях: а) по проводу в течение t = 24 с протекал постоянный ток; б) ток в проводе убывал до нуля таким образом, что за каждые t = 24 с он убывал вдвое.

19. Через свинцовую проволоку диаметром d = 0,2 мм пропускается ток I = 0,5 А. Определить: а) какой промежуток времени пройдет до того момента, когда проволочка начнет плавиться. Удельная теплоемкость свинца 126 Дж/(кгК), удельное сопротивление 0,22 мкОмм, плотность 11,3 г/см³, температура плавления t = 327 С. Пренебречь потерей теплоты во внешнее пространство. Принять начальную температуру проволочки равной 0 С; б) какой промежуток времени пройдет до начала плавления проволоки, если по ней идет ток I = 0,5cos(100t) А.

20. При Т = 473 К и Р = 0,999·10⁵ Н/м² 7,1610^–4 кг органическое вещество, испаряясь, занимает объем 2,42610^–4 м³. Вычислить молярную массу соединения и определить его формулу, если С : Н : О = 2,25 : 0,375 :1.

21. Какое количество тепла Q нужно сообщить 75 г водяных паров, чтобы нагреть их от 100 до 250 С при постоянном объеме?

22. 1 м³ водорода при 0 С находится в цилиндрическом сосуде, закрытом сверху легкоскользящим невесомым поршнем. Атмосферное давление 730 мм рт. ст. Какое количество тепла Q потребуется на нагревание водорода до 300 С?

23. Смешано m = 4,032 г водорода с m₁ = 32 г кислорода. Их удельные теплоемкости c_P = 3,50 кал/(гС) и c_P1 = 0,218 кал/(гС). Определить уменьшение внутренней энергии U этой смеси при охлаждении ее на t = 20 С при постоянном объеме. Для обоих газов  = 1,40.

24. В объеме V₀ при температуре t = 0 С содержится  молей водорода и /2 молей кислорода. Найти выражение для максимального давления Р_m при той же температуре водяного пара, полученного при взрыве смеси, если молярная теплоемкость водяного пара С, а молярная теплота образования воды из кислорода и водорода Q.

25. Два теплоизолированных сосуда с объемами V₁ = 1 л и V₂ = 3 л соединены трубкой с краном. До открытия крана в первом сосуде содержался азот под давлением P₁ = 0,5 атм при температуре t₁ = 0 С, а во втором – аргон под давлением P₂ = 1,5 атм при температуре t₂ = 100 С. Определить, какие давление и температура установятся в смеси газов, если открыть кран.

26. Определить удельную теплоемкость c_V смеси 50 % по весу водорода и гелия, заключенной в объеме V = 1 л при температуре 27 С и давлении Р = 800 мм рт. ст. Молярные теплоемкости водорода H₂ C_Vl = 5 кал/(мольС) и гелия C_V2 = 5 кал/(мольС).

27. Найти молярную массу молекул идеального газа, если известны его удельные теплоемкости: c_V = 0,65 Дж/(гК) и c_P = 0,91 Дж/(гК).

28. Подсчитать по классической теории удельную теплоемкость при постоянном давлении газа следующего молярного состава:

Не – 20 %; Н₂ – 30 %; СН₄ – 50 %.

(Молярный состав указывает отношение количества молей данного газа к общему количеству молей всей смеси газов.)

29. Вычислить удельную теплоемкость воздуха при постоянном объеме, считая его смесью кислорода О₂ и азота N₂ с отношением масс компонентов 23:77. Удельная теплоемкость газообразного кислорода при постоянном объеме равна 0,158 кал/гград, а газообразного азота 0,176 кал/гград.

30. В сосуде емкостью V = 10 л находится кислород О₂ под давлением Р₀ = 1 атм. Стенки сосуда могут выдержать давление до Р₁ = 10 атм. Какое максимальное количество тепла Q можно сообщить газу?

31. Воздух, находящийся в трубке «воздушного огнива» при температуре t₁ = 17 °С, подвергается адиабатному сжатию от давления Р₁ = 1 атм до давления Р₂ = 10 атм. Найти температуру воздуха после сжатия, если отношение для воздуха равно 1,4. Считать применимым уравнение адиабаты. «Воздушным огнивом» называется закрытый с одного конца цилиндр с толстыми адиабатическими стенками, внутрь которого можно быстро вдвигать поршень и таким путем воспламенять пары эфира, подмешанные к воздуху. (Вместо эфира можно взять кусочек пироксилиновой ваты, положенный на дно цилиндра или прикрепленный к поршню.)

32. Для определения иногда применяется следующий метод. Определенное количество газа, начальная температура, объем и давление которого соответственно равны t₀, V₀ и Р₀, нагревается платиновой проволокой, через которую проходит электрический ток в течение энного времени: один раз при постоянном объеме, причем газ достигает температуры t₁ и давления Р₁ (объем V₀), другой раз при постоянном давлении, причем температура становится равной t₂, а объем V₁ (давление Р₀). Показать, что

33. Для определения отношения удельных теплоемкостей c_P и c_V газа измерили период T₁ малых колебаний ртути в U-образной стеклянной трубке с незапаянными концами. После этого на обе ветви трубки были насажены большие одинаковые полые стеклянные шары с исследуемым газом, вследствие чего период колебаний изменился и стал равным T₂. Считая процесс сжатия и разрежения газа в шарах адиабатическим, вывести формулу для . Объем каждого шара равен V см³, давление газа в них в состоянии покоя h см рт. ст., а площадь поперечного сечения трубки S см². Объемом незаполненной части трубки можно пренебречь по сравнению с объемом шара V.

34. Рассмотреть вертикальный столб воздуха бесконечной высоты и постоянного сечения. Вычислить его теплоемкость, считая воздух идеальным газом, находящимся в постоянном гравитационном поле.

35. Согласно теории теплоемкостей Дебая свободная анергия твердого тела при низких температурах выражается формулой

,

где U₀ – внутренняя энергия тела при абсолютном нуле (нулевая энергия), а A – положительный коэффициент, зависящий только от объема V. Пользуясь этой формулой, показать, что при низких температурах отношение коэффициента объемного расширения тела  к теплоемкости C_V не зависит от температуры (закон Грюнейзена).

36. Для получения газов при сверхвысоких температурах и давлениях иногда применяют установку, состоящую из закрытого с одного конца цилиндра-ствола и поршня-пули, влетающей в цилиндр с открытой стороны. При хорошей обработке ствола и пули удается добиться малой утечки газа через зазор. Благодаря очень высоким температурам сильно сжатые газы в этих условиях еще можно считать идеальными. Оценить верхний предел температуры T, давления P и плотности  аргона, подвергнутого сжатию в такой установке, если пуля массой m  100 г влетает в ствол, имеющий объем V  200 см³, с начальной скоростью v  250 м/с. Начальная температура и давление соответственно равны: T₀  300 К и P₀  1 атм.

37. В длинной вертикальной цилиндрической трубке, закрытой с нижнего конца, может ходить без трения поршень, масса М которого велика по сравнению с массой газа, заключенного внутри трубки. В положении равновесия расстояние между поршнем и дном трубки равно l₀. Определить период малых колебаний, которые возникнут при отклонении поршня из положения равновесия, в предположении, что они являются изотермическими, а газ идеальным. Площадь поперечного сечения трубки равна S, нормальное атмосферное давление P₀. Рассмотреть предельный случай, когда P₀ = 0.

38. Решить предыдущую задачу в предположении, что колебания – адиабатические. Будет ли сказываться на результате зависимость показателя адиабаты  для газа от температуры?

39. Пылинки, взвешенные в воздухе, имеют массу 10^–18 г. Во сколько раз уменьшается их концентрация при увеличении высоты на 1 м? Температура воздуха Т = 300 К.

40. Определить массу одной из пылинок, взвешенных в воздухе, если в толщине слоя воздуха 3 см их концентрация различается на 35 % при температуре 22 С.

41. Найти массу моля коллоидных частиц, если при вращении центрифуги с угловой скоростью  вокруг вертикальной оси концентрация этих частиц на расстоянии r₂ от оси вращения в  раз больше, чем на расстоянии r₁ (в одной горизонтальной плоскости). Плотности частиц и растворителя равны соответственно  и ₀.

42. Горизонтально расположенную трубку с закрытыми торцами вращают с угловой скоростью  вокруг вертикальной оси, проходящей через один из ее торцов. В трубке находится углекислый газ при T = 300 К. Длина трубки l = 100 см. Найти , при котором отношение концентраций молекул у противоположных торцов трубки  = 2,0.

43. Частицы некоторого твердого вещества взвешены в жидкости. Среднее их число в слоях, расстояние между которыми 54 мкм, отличается друг от друга в два раза. Температура среды 330 К. Диаметр частиц 0,4 мкм. На сколько плотность вещества частиц больше плотности жидкости?

44. В некоторой жидкости взвешены частицы твердого вещества, плотность которого 2 г/см³. Концентрации частиц в слоях, расстояние между которыми 16 мкм, отличаются друг от друга в 3 раза. Температура жидкости 277 К. Радиус частиц 0,2 мкм. Определить плотность жидкости.

45. В центрифуге находится некоторый газ при температуре 300 К. Ротор центрифуги радиуса 0,4 м вращается с угловой скоростью 500 рад/с. Определить массу одного моля газа, если давление у стенки ротора в 1,38 раза больше давления в его центре.

46. Ротор ультрацентрифуги радиуса 0,2 м заполнен атомарным ураном при температуре 3000 К. Уран состоит из двух изотопов: урана-235 и урана-238. Доля урана-235 в центре ротора центрифуги составляет 7 %. Определить долю урана-235 вблизи стенок ротора, если ему сообщить угловую скорость вращения 10⁴ рад/с.

47. Цилиндрическая центрифуга вращается с частотой n = 2500 с^-1. Диаметр цилиндра равен 2r₀ = 0,2 м. В цилиндре находится эмульсия из УДА и воды. Относительная молярная масса УДА и плотность УДА соответственно μ = 12 г/моль; ρ_УДА = 3,5 г/см³. Определить отношение плотностей распределения на периферии (r = r₀ ) и на оси (r = 0).

48. Для определения коэффициента объемного расширения  стекла взвешивают небольшой стеклянный баллон с оттянутым кончиком – сначала густой, а затем с количеством ртути, необходимым для наполнения всего баллона при двух температурах, например 0 С и t. Пусть m₀ и m₁ – массы ртути при указанных температурах. Определить коэффициент объемного расширения стекла ее, если коэффициент объемного расширения ртути ₁.

49. Стеклянный шарик с коэффициентом объемного расширения α взвешивают в жидкости при температурах t и t₁. Массы вытесненной жидкости соответственно m и m₁. Определить коэффициент объемного расширения жидкости ₁ в интервале температур от t до t₁.

50. Пикнометр при некоторой температуре t заполнен спиртом, масса которого равна m. Затем пикнометр вместе со спиртом нагревают до температуры t₁, излишек спирта против прежнего уровня удаляют фильтровальной бумагой. После этого масса спирта оказалась равной m₁. Определить средний коэффициент объемного расширения спирта , если коэффициент линейного расширения стекла .

51. Для определения истинного коэффициента объемного расширения жидкостей применяют следующий метод. Два сообщающихся сосуда наполняют жидкостью, расширение которой исследуют; при одинаковой температуре обоих сосудов жидкость в них находится на одной высоте. Если один из сосудов охлаждать тающим льдом, а другой нагревать в парах кипящей при нормальном атмосферном давлении воды, то при равновесии уровни жидкостей будут различны. Эта разность уровней дает возможность вычис­лить коэффициент объемного расширения . Вывести выражение для .

52. Колесо паровоза имеет радиус r₀ = 1 м при t₀ = 0 °C. Определить разницу в числах оборотов колеса летом при температуре t₁ = 25 С и зимой при температуре t₂ = –25 С на пути пробега паровоза l = 100 км. Коэффициент линейного расширения металла колеса  = 0,000012 С^–1.

53. Из кварца параллельно его оси вырезана круглая пластинка, радиус которой при температуре t₁ равен r. Определить площадь пластинки S при температуре t₂. Коэффициент линейного расширения кварца параллельно оси – , а перпендикулярно к ней – .

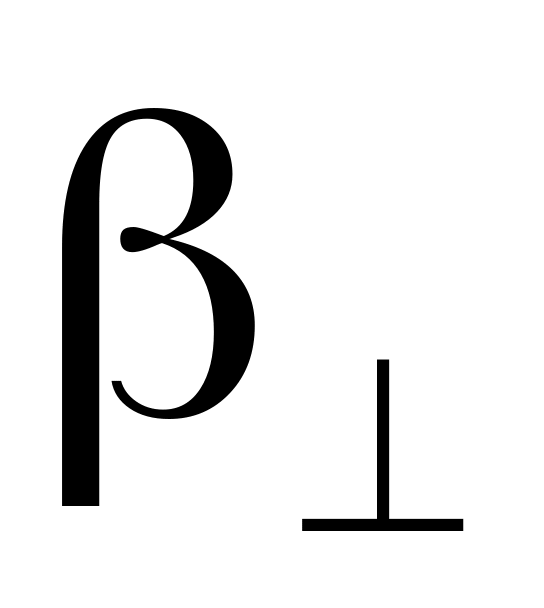54. Из кварца вырезан цилиндр, ось которого параллельна оси кварца. При температуре t₁ = 18 С радиус цилиндра r =10 мм, а высота l = 50 мм. Определить объем этого цилиндра V₂ при температуре t₂ = 300 С. Для кварца коэффициент линейного расширения = 0,000072 С^–1, a = 0,0000132 С^–1.

55. Коэффициент объемного расширения ртути  при 0 С и атмосферном давлении равен 0,00018 С^–1. Сжимаемость  = 0,0000039 атм^–1. Вычислить температурный коэффициент давления  для ртути.

56. На сколько надо увеличить внешнее давление, чтобы сохранить постоянным объем ртути при нагревании ее от 0 до 10 С. (См. предыдущую задачу.)

57. Какую силу F надо приложить к стальному стержню сечением в 1 см², чтобы растянуть его настолько же, насколько он удлиняется при нагревании на t = 1 С. Коэффициент линейного расширения  = 1210^–6 С^–1. Модуль Юнга E = 2,110⁷ Н/см².

58. Стальной бандаж надевают на вагонное колесо при температуре t₁ = 300 С. Определить силу натяжения Т в бандаже при температуре t₀ = 20 С, если сечение бандажа S = 20 см². Модуль Юнга E = 2,110⁷ Н/см² и коэффициент линейного расширения  = 1210^–6 С^–1.

59. Найти плотность  морской воды на глубине 5 км, если на поверхности океана плотность ₀ = 1,03 г/см³, а сжимаемость воды в пределах давлений от 1 до 500 атм равна  = 45,710^–7 атм^–1.

60. Какое максимальное давление может произвести вода при замерзании? Плотность льда ₀ = 0,917 г/см³, модуль Юнга для льда E = 2,810¹¹ дин/см², коэффициент Пуассона  = 0,3.

61. Какое давление необходимо приложить к торцам стального цилиндра, чтобы длина его не изменилась при повышении температуры на 100 °С?

62. Доказать, что внутреннюю энергию и и энтальпию h единицы массы идеального газа с постоянной удельной теплоемкостью можно записать в форме , , где – скорость звука (р – давление,  – плотность, производная вычисляется для адиабатического процесса),  – отношение удельной теплоемкости при постоянном давлении к удельной теплоемкости при постоянном объеме.

63. Найти конечную температуру Т₂ и верхний предел скорости v стационарного потока углекислого газа СО₂, вытекающего через сопло в атмосферу из баллона, где он имел температуру T₁ = 300 К и находился под давлением P₁ = 10 атм, если давление наружного воздуха Р₂ = 1 атм. Показатель адиабаты для СО₂ равен  = 1,30, удельная теплоемкость с_Р = 0,202 кал/(гС).

Указание: применить уравнение Бернулли.

64. Воздух, сжатый в большом баллоне при температуре T₁ = 273 К, вытекает в атмосферу по трубке, в конце которой он приобретает скорость v = 400 м/с. Найти температуру вытекающего воздуха T₂ в конце трубки, а также давление P₁ воздуха в баллоне. Процесс истечения газа считать адиабатическим.

65. Определить максимальную скорость, которую может достигнуть газ при адиабатическом истечении из баллона, если абсолютная температура газа в баллоне равна Т.

66. Найти конечную температуру T₂ и верхний предел скорости v стационарного потока перегретого пара, вытекающего через сопло в атмосферу из камеры, где он имел температуру T₁ = 600 К и находился под давлением P₁ = 5 атм, если давление наружного воздуха P₂ = 1 атм. Перегретый пар считать идеальным газом с молярной теплоемкостью С_P = 4R.

67. Допустим, что температура горения химического горючего для ракетных двигателей T = 3000 К, средняя относительная молекулярная масса продуктов горения  = 30 и истечение продуктов горения происходит в вакууме адиабатически. Найти, во сколько раз стартовая масса одно­ступенчатой ракеты M₀ должна превышать ее конечную массу М, чтобы ракета могла достичь первой космической скорости v = 8 км/с. Молярную теплоемкость продуктов горения ориентировочно принять равной С_P = 8 кал/(моль°С). При вычислении скорости ракеты силу тяжести и трение о воздух не учитывать.

68. Тело (например, космический корабль) движется в идеальном газе со скоростью v. В какой точке тела температура газа будет максимальной? Определить эту температуру, если температура окружающего газа равна Т.

69. Вольфрамовая нить, испаряясь в высокий вакуум при температуре Т = 2000 К, уменьшается в массе, как показали измерения, со скоростью q = 1,1410^–13 г/(ссм²). Вычислить давление насыщенного пара вольфрама при этой температуре.

70. Какова была бы мгновенная скорость испарения воды с каждого квадратного сантиметра ее поверхности, если бы над этой поверхностью был вакуум, а температура воды в этот момент равнялась Т = 300 К? Табличное значение упругости насыщенного водяного пара при этой температуре Р = 27 мм рт. ст. Сравнить полученную величину с величиной скорости испарения воды при обычных условиях (т. е. когда над ее поверхностью находится воздух при нормальном давлении) и объяснить получившееся расхождение.

71. Для определения поверхностного натяжения воды взвешивают капли, отрывающиеся от капилляра, и измеряют диаметр d шейки капли в момент отрыва. Оказалось, что масса 318 капель воды равна 5 г, a d = 0,7 мм. Найти поверхностное натяжение воды.

72. Как велико поверхностное натяжение о жидкость, если петля из резинового шнура длиной l с поперечным сечением S, положенная на пленку этой жидкости, растянулась в окружность радиуса R после того, как пленка была проколота внутри петли? Считать, что при малых растяжениях для резины справедлив закон Гука и модуль Юнга резины равен E.

73. Найти выражение для внутренней энергии U пленки.

74. Определить изменение температуры пленки при адиабатическом расширении.

75. Мыльная пленка имеет толщину h = 10^–3 мм и температуру T = 300 К. Вычислить понижение температуры этой пленки, если ее растянуть адиабатически настолько, чтобы площадь пленки удвоилась. Поверхностное натяжение мыльного раствора убывает на 0,15 дин/см при повышении температуры на 1 К.

76. В сосуде с адиабатическими стенками находится мыльный пузырь радиуса r = 5 см. Общее количество воздуха в сосуде и в пузыре  = 0,1 моля, его температура T = 290 К (предполагается, что она одинакова внутри и вне пузыря). При этой температуре поверхностное натяжение  = 70 дин/см, d/dT = –0,15 дин/(смК). Как изменится температура воздуха в сосуде, если пузырь лопнет? Теплоемкостью образовавшихся капелек пренебречь.

77. Чему равно капиллярное давление P в капельке ртути диаметром d = l мкм при температуре 15 С, если поверхностное натяжение ртути при этой температуре  = 487 дин/см?

78. Чему равно добавочное давление Р внутри мыльного пузыря диаметром d = 0,8 см, если поверхностное натяжение мыльной воды  =  = 40 дин/см?

79. В дне сосуда имеется трещина шириной a = 0,02 мм. До какой высоты h можно налить ртуть в сосуд, чтобы она не вытекала через трещину? Плотность ртути  = 13,6 г/см³. Поверхностное натяжение (при 15 С)  =  = 487 дин/см.

80. Оценить максимальное количество воды, которое можно налить в решето с парафинированным дном диаметром D = 20 см, если последнее сделано из металлического листа с круглыми отверстиями диаметром d = 1 мм. Поверхностное натяжение воды  = 70 дин/см. Как зависит максимальное количество наливаемой жидкости от ее плотности?

81. Чтобы стряхнуть ртуть в медицинском термометре, нужно ускорение a ~ 10g. Оценить диаметр перетяжки в капилляре термометра. Поверхностное натяжение ртути  = 490 дин/см, длина столбика ртути выше перетяжки h ~ 5 см, плотность ртути  = 13,6 г/см³.

82. На дне пруда глубиной h = 2 м выделяются пузырьки газа диаметром d₁ = 0,05 мм. Чему будут равны диаметры d₂ этих пузырьков, когда они поднимутся к поверхности воды? Поверхностное натяжение воды  = 73 дин/см.

83. На какую величину T температура воздуха внутри мыльного пузыря должна превышать температуру окружающего воздуха Т, чтобы пузырь стал подниматься? Радиус пузыря равен r, поверхностное натяжение мыльной пленки . Массой пленки можно пренебречь. Учесть, что давление воздуха внутри пузыря мало отличается от атмосферного давления P.

84. Мыльный пузырь выдут через цилиндрическую трубку внутреннего радиуса r = 1 мм и длиной l = 10 см. В тот момент, когда радиус пузыря достигает значения R₀ = 10 см, перестают дуть, и воздух из пузыря начинает выходить через трубку. Через какое время, начиная с этого момента, пузырь исчезнет? Поверхностное натяжение мыльного раствора  = 50 дин/см, вязкость воздуха  = 1,810^–4 динс/см². Изменением плотности воздуха за время процесса пренебречь.

85. В стенке шарового мыльного пузыря сделано круглое отверстие радиуса a =1 мм (такое отверстие, например, можно получить, поместив на стенку пузыря петельку из нити, а затем проткнув мыльную пленку внутри этой петельки). Найти время, в течение которого весь воздух выйдет из пузыря, если его начальный радиус r₀ = 10 см. Температура воздуха вне и внутри пузыря t = 20 С. Поверхностное натяжение мыльного раствора при этой температуре  = 50 дин/см. Атмосферное давление P = 750 мм рт. ст. Среднюю относительную молекулярную массу воздуха принять равной  = 29. При истечении через отверстие воздух рассматривать как идеальную несжимаемую жидкость.

86. Какова разность уровней жидкости в двух сообщающихся капиллярах диаметрами d₁ и d₂. Поверхностное натяжение жидкости равно . Краевые углы менисков равны нулю. Плотность жидкости .

87. Насколько изменится разность уровней h₁–h₂ воды в двух сообщающихся капиллярах диаметрами d₁ = 0,1 мм и d₂ = 0,3 мм при нагревании от 20 до 70 С, если поверхностное натяжение воды для этих температур равно соответственно 73 и 64 дин/см?

88. Капля воды массой m = 0,1 г введена между двумя плоскими и параллельными между собой стеклянными пластинками, смачиваемыми водой, причем краевой угол  = 0°. Как велика сила притяжения между пластинками F, если они находятся друг от друга на расстоянии d = 10^–4 см? Поверхностное натяжение воды (при 18 С)  = 73 дин/см.

89. Грамм ртути помещен между двумя плоскими стеклянными пластинками. Какую силу F надо приложить к верхней пластинке, чтобы ртуть приняла форму круглой лепешки однородной толщины и радиуса R = 5 см. Поверхностное натяжение ртути (при 15 С)  = 487 дин/см, краевой угол между ртутью и стеклом  = 40°.

90. В закрытом сосуде при 0 С находится один моль (18 г) воды. Какое количество тепла надо затратить, чтобы повысить температуру системы до 100 С и чтобы при этом вся вода превратилась в насыщенный пар. Удельная теплота испарения воды при 100 С и постоянном давлении составляет 539 кал/г. Упругостью насыщенного пара при 0 С и теплоемкостью стенок сосуда пренебречь. Пренебречь также объемом воды по сравнению с объемом ее насыщенного пара.

91. На дне сосуда, откачиваемого до высокого вакуума, наморожен плоскопараллельный слой льда толщиной l = 7 мм, нижняя поверхность которого поддерживается при постоянной температуре t₀. Определить эту температуру, если известно, что при откачке сосуда на верхней поверхности слоя льда установилась температура t₁ = –50 С. Теплопроводность льда  = 5,310^–3 кал/(ссмС). Удельная теплота сублимации льда q = 680 кал/г. Упругость насыщенного пара над льдом при t₁ = –50 С в отсутствие откачки равна P = 0,03 мм рт. ст.

92. Найти коэффициент объемного расширения , изотермическую сжимаемость _т и теплоемкость C_P неоднородной равновесной системы, состоящей из жидкости и ее насыщенного пара.

93. Рассмотрите систему, состоящую из жидкости и ее насыщенного пара, и выразите производную давления насыщенного пара по температуре dP/dT через удельные объемы пара и жидкости v_п, v_ж и удельную теплоту парообразовании q.

94. Найти изменение температуры T плавления льда при повышении давления на P = 1 атм. Удельный объем воды при 0 С v_ж = 1 см³/г, удельный объем льда v_ж = 1,091 см³/г, удельная теплота плавления льда q = 80 кал/г. По найденному значению T рассчитать приближенно температуру тройной точки воды.

95. Ромбическая сера превращается в моноклинную при t = 96,5 С. При атмосферном давлении удельная теплота превращения q = 2,2 кал/г. Скачок удельного объема серы при фазовом превращении v = 0,014 см³/г. Найти смещение T точки фазового перехода серы при изменении давления на P = 1 атм.

96. Найти давление насыщенного водяного пара при температуре 101 С. Считать пар идеальным газом.

97. В закрытом сосуде объемом V₀ = 5 л находится 1 кг воды при температуре t =100 С. Пространство над водой занято насыщенным водяным паром (воздух выкачан). Найти увеличение массы насыщенного пара m при повышении температуры системы на T = 1 К. Удельная теплота парообразования q = 539 кал/г.

Указание: при расчетах пар считать идеальным газом. Удельным объемом воды пренебречь по сравнению с удельным объемом пара.

98. При 0 С упругость водяного пара над льдом P₁ = 4,58 мм рт. ст. Удельная теплота плавления льда при 0 С q₁ = 80 кал/г. Теплота испарения воды при 0 С q₃ = 596 кал/г. Найти упругость водяного пара над льдом при температуре t = –1 С.

99. Найти удельную теплоту испарения бензола q_исп вблизи его тройной точки, если известно, что при этих условиях его удельная теплота плавления q_пл = 30,2 кал/г, температура тройной точки T = 279 К, равновесное давление пара в тройной точке P = 36 мм рт. ст. и для кривой возгонки в той же точке dP/dT = 2,43 мм рт. ст/K. Считать пар бензола идеальным газом.

100. Уксусная кислота при атмосферном давлении плавится при температуре t = 16,6 °С. Разность удельных объемов жидкой и твердой фаз уксусной кислоты v = 0,16 см³/г. Точка плавления уксусной кислоты смещается на T = 1 К при изменении давления на P = 41 атм. Найти удельную теплоту плавления q уксусной кислоты.

101. Кусок льда помещен в адиабатическую оболочку при температуре 0 С и атмосферном давлении. Как изменится температура льда, если его адиабатически сжать до давления P = 100 атм? Какая доля льда m/m при этом расплавится? Удельные объемы воды v_в = l см³/г, льда v_л = 1,09 см³/г. Теплоемкости воды и льда связаны соотношением с_л 0,6с_в.

102. Найти зависимость давления насыщенного пара от температуры в следующих упрощающих предположениях: удельную теплоту парообразования q считать не зависящей от температуры; удельный объем жидкости пренебрежимо мал по сравнению с удельным объемом пара; к жидкости применимо уравнение состояния Клапейрона. (Эти упрощения допустимы вдали от критической температуры, если интервал изменения температур не слишком широк.)

103. Вывести формулу, выражающую зависимость давления насыщенного пара от температуры при следующих предположениях: 1) пар подчиняется уравнению состояния Клапейрона; 2) удельная теплота испарения q является линейной функцией температуры, т. е. q = q₀–T; 3) удельный объем жидкости пренебрежимо мал по сравнению с удельным объемом насыщенного пара.

104. Найти повышение температуры кипения воды при увеличении давления ее насыщенного пара на одну избыточную атмосферу вблизи точки кипения воды в нормальных условиях. Удельная теплота испарения воды в этих условиях q = 539 кал/г.

105. В закрытом сосуде при температуре t = 20 °С находился влажный воздух с относительной влажностью f = 80 %. На сколько градусов надо понизить температуру стенок сосуда, чтобы на них начала выпадать роса? Удель­ная теплота парообразования воды при 20 °С q = 500 кал/г. Водяной пар рассматривать как идеальный газ.

106. В тонкостенный металлический шар радиуса r = 10 см, из которого выкачан воздух, налита вода. Давление воздуха вне шара равно атмосферному. До какой максимальной температуры можно нагреть воду, чтобы стенки шара не разорвались, если предельное натяжение на разрыв, которое они могут выдержать,  = 88 Н/см. Количество воды в шаре таково, что при этой температуре еще не вся вода испаряется, однако объем воды мал по сравнению с объемом пара.

107. Стакан наполнен водой до высоты 10 см. На дне его лежат капиллярные трубки, запаянные с одного конца и заполненные воздухом. Когда вода кипит, на открытых концах капилляров образуются пузырьки пара, диаметр которых в момент отрыва равен 0,2 мм. Чему равна температура воды на дне сосуда во время кипения, если атмосферное давление равно 760 мм рт. ст.? Поверхностное натяжение кипящей воды 57 дин/см, а уп­ругость водяного пара вблизи 100 °С возрастает на 2,7 см рт. ст. при повышении температуры на 1 С.

108. Вычислить давление насыщенного водяного пара над сферической поверхностью капли воды радиуса: 1) r₁ = 10^–5 см (капелька тумана), 2) r₂ = 10^–7 см при 20 С. При такой температуре для воды  = 72,7 дин/см, v_ж  = 1,002 см³/г, P₀ = 17,5 мм рт. ст.

109. Найти стационарный поток пара от сферической капли жидкости радиуса a в процессе ее испарения (или конденсации пара на капле). Коэффициент диффузии паров жидкости в воздухе равен D, плотность пара на большом расстоянии от капли _, плотность насыщенного пара _н. Найти также плотность пара  в зависимости от расстояния r от центра капли. Зависимость упругости насыщенного пара от кривизны поверхности жидкости не учитывать.

110. При прохождении через перегретую жидкость ионизующей частицы вдоль ее траектории образуются мельчайшие пузырьки пара. Те из пузырьков, радиус которых больше «критического радиуса» R_кр, быстро вырастают до видимых размеров, а пузырьки меньших размеров захлопываются силами поверхностного натяжения. Определить R_кр для жидкого пропана (C₃H₈), если в камере он находится под давлением Р_ж = 5 атм при температуре Т = 328 К. Давление насыщенного пара пропана при этой температуре Р_н = 15 атм, поверхностное натяжение пропана _п = 4,46 дин/см.

111. 1 г водорода, сгорая и превращаясь в воду, выделяет 34000 кал тепла. Сколько угля надо сжечь для диссоциации 1 г воды, если из выделяемой углем теплоты используется 50 %? Удельная теплота сгорания угля равна 3000 кал/г.

112. При сгорании 12 г твердого углерода в углекислый газ CO₂ выделяется 410 кДж, а при сгорании 28 г окиси углерода CO выделяется 290 кДж. Какое количество тепла выделилось бы при сгорании 12 г твердого углерода, если бы в результате сгорания получалась только чистая окись углерода?

113. При сгорании водорода при 100 C с образованием одного моля водяного пара выделяется Q₁ = 58000 кал. При конденсации одного моля водяного пара при 100 С выделяется Q₂ = 9700 кал. Найти теплоту образования одного моля жидкой воды Q из водорода и кислорода при той же температуре.

114. При полном сгорании моля метана в углекислоту и воду выделяется Q₁ = 887 кДж. При образовании из элементов моля воды выделяется Q₂ = 287 кДж, а при полном сгорании углерода с образованием моля СО₂ выделяется тепло Q₃ = 407 кДж. Определить теплоту Q образования моля метана из твердого углерода и газообразного водорода.

115. Стальной стержень длиной l = 20 см и площадью поперечного сечения S = 3 см² нагревается с одного конца до температуры t₁ = 300 °C, а другим концом упирается в лед. Предполагая, что передача тепла происходит исключительно вдоль стержня (без потерь через стенки), подсчитать массу т льда, растаявшего за время  = 10 мин. Теплопроводность стали  = 0,16 кал/(ссмС).

116. Три пластинки одинакового размера сложены вместе, образуя столбик. В середине – свинцовая пластинка, по краям – серебряные. Внешняя сторона одной серебряной пластинки поддерживается при постоянной температуре t = 100 С. Внешняя сторона другой серебряной пластинки имеет температуру t₃ = 0 С. Найти температуры t₁ и t₂ в местах соприкосновения свинцовой пластинки с серебряными. Теплопроводности свинца ₁ = 30 ккал/(чм°С), серебра ₂ = 360 ккал/(чм°С).

117. Пространство между двумя коаксиальными цилиндрами радиусов R₁ и R₂ заполнено проводящим тепло однородным веществом. Найти распределение температуры в этом пространстве, если температура внутреннего цилиндра t₁, а внешнего t₂.

118. Найти распределение температуры в пространстве между двумя концентрическими сферами радиусов R₁ и R₂, заполненном проводящим тепло однородным веществом, если температуры обеих сфер постоянны и равны t₁ и t₂.

119. Стержень сечения S упирается концами в твердые пластины, расстояние L между которыми поддерживается постоянным. Затем температуру одной из пластин повышают, и в стержне устанавливается постоянный поток тепла Q. Какое давление Р действует на единицу поперечного сечения стержня, если начальное напряжение в стержне было равно нулю? Теплопроводность стержня , коэффициент линейного расширения , модуль Юнга Е.

120. Сферический кусок льда (начальный радиус R₀ = 1 см) погружен в большую массу воды температурой 10 °С. Предполагая, что теплопередача в жидкости связана только с ее теплопроводностью, определить время , в течение которого лед полностью растает. Теплопроводность воды  = 610^–3 Дж/(ссмС), удельная теплота плавления льда q = 330 Дж/г.

121. Определить толщину льда, образующегося в течение заданного времени t на спокойной поверхности озера. Считать, что температура Т окружающего воздуха все время постоянна и равна температуре наружной поверхности льда (T < T_пл, где Т_пл – температура плавления льда). Произвести численный расчет, предполагая, что Т = –10 С. Для льда  = 2,2210⁵ эрг/(ссмС), q = 3,3510⁹ эрг/г,  = 0,9 г/см³.

122. На концах длинного однородного стержня, поперечные размеры которого малы по сравнению с его длиной, задаются температуры t₁ и t₂, которые могут меняться во времени. Температура однородной среды, окружающей стержень, равна t₃. Показать, что благодаря теплообмену температура в стержне подчиняется уравнению

,

где , , р – периметр поперечного сечения стержня, S – площадь этого сечения, с – удельная теплоемкость вещества стержня,  – его плотность,  – коэффициент теплообмена,  – теплопроводность.

123. Найти установившееся распределение температуры вдоль длинного и очень тонкого стержня длиной l, если температуры его концов t₁ и t₂, а также температура окружающей среды t₃ поддерживаются постоянными. Остальные величины: , , р – периметр поперечного сечения стержня, S – площадь этого сечения, с – удельная теплоемкость вещества стержня,  – его плотность,  – коэффициент теплообмена,  – теплопроводность.

124. Решить предыдущую задачу в предположении, что t₃ = t₂. Рассмотреть случай очень длинного стержня.

125. Вычислить температуру средней точки круглого стержня длиной l = 80 см, радиуса r = 2 см с теплопроводностью  = 0,8 кал/(ссмС) и коэффициентом теплообмена  = 510^–4 кал/(ссм²С), если оба конца стержня поддерживаются при одной и той же температуре t₁ = t₂ = 100 °C, а температура комнаты t₃ = 20 °C.

126. Для определения теплопроводностей жидкостей используются три медные пластинки, расположенные горизонтально одна над другой. Нижняя пластинка омывается потоком холодной воды (температура t₁), верхняя – теплой (температура t₃). Пространство между нижней и средней пластинками заполнено жидкостью с теплопроводностью ₁, а пространство между средней и верхней – жидкостью с теплопроводностью ₂. Расстояние средней пластинки от нижней равно d₁, а от верхней – d₂. Выразить теплопроводность ₂ через ₁, если в установившемся состоянии температура средней пластинки равна t₂. В случае, когда в качестве известной жидкости взята вода ( = 0,00143 кал/(ссмС), а в качестве испытуемой – бензол, для расстояний d₁ = 1 мм и d₂ = 1,2 мм получились температуры: t₁ = 80 С, t₂ = 68,6 °С, t₃ = 10 С. Найти ₂ для бензола.

127. Полупространство x > 0 заполнено веществом с температуропроводностью . В плоскости x = 0 происходят гармонические колебания температуры с периодом Т, тогда

,

где t₀ и t₁ – постоянные, а . Найти температуру среды в зависимости от координаты x и времени .

Указание: искать решение уравнения теплопроводности в комплексной форме: , а затем перейти к вещественной форме.

128. Определить количество тепла Q, теряемое 1 м² стены в течение времени , равного одним суткам, при температуре воздуха в помещении t₁ = 20 С и температуре наружного воздуха t₄ = –10 С. Толщина стены l = 20 см. Теплопроводность материала стены  = 0,003 кал/(ссмС). Коэффициент теплообмена на границе стена – воздух  = 0,0002 кал/(ссм²С). Определить также температуры внутренней t₂ и внешней t₃ поверхностей стены.

129. Горизонтально расположенный медный стержень длиной l = 1,0 м вращают вокруг вертикальной оси, проходящей через его середину. При какой частоте вращения он может разорваться?

130. Кольцо радиуса r = 25 см, сделанное из свинцовой проволоки, вращают вокруг неподвижной вертикальной оси, проходящей через его центр и перпендикулярной плоскости кольца. При какой частоте вращения данное кольцо может разорваться?

131. Стальная проволока диаметром d = 1,0 мм натянута в горизонтальном положении между двумя зажимами, находящимися на расстоянии l = 2,0 м друг от друга. К середине проволоки – точке О – подвесили груз массой т = 0,25 кг. На сколько сантиметров опустится точка О?

132. Однородный упругий брусок движется по гладкой горизонтальной плоскости под действием постоянной силы F₀, равномерно распределенной по торцу. Площадь торца S, модуль Юнга материала Е. Найти относительное сжатие бруска в направлении действия данной силы.

133. Тонкий однородный медный стержень длиной l и массой т равномерно вращается с угловой скоростью  в горизонтальной плоскости вокруг вертикальной оси, проходящей через один из его концов. Найти силу натяжения в стержне в зависимости от расстояния r до оси вращения, а также удлинение стержня.

134. Сплошной медный цилиндр длиной l = 65 см поставили на горизонтальную поверхность и сверху приложили вертикальную сжимающую силу F = 1000 H, которая равномерно распределена по его торцу. На сколько кубических миллиметров изменился объем цилиндра?

135. Медный стержень длиной l подвесили за один конец к потолку.

Найти:

а) удлинение стержня под действием собственного веса;

б) относительное приращение его объема V/V.

136. Сферический баллон радиуса R со стенками толщиной  << R разрывается внутренним давлением Р. Определить предел прочности материала стенок.

137. В сферической стальной (Ст3) оболочке радиуса R = 64,2 см и толщиной  = 4,5 см взрывается центрально расположенный сферический заряд гексогена (₀ = 1,2 г/см³, Q = 1350 кал/г) массой G = 2 кг. Найти частоту и период колебаний, период циркуляции упругой волны, величину радиальных смещений, скорость смещений, ускорение движения стенки оболочки камеры и эквивалентное напряжение в материале оболочки.

138. В цилиндрической стальной камере (длина обечайки 400 см, радиус R = 80 см, толщина стенки оболочки =9 см) с полусферическими днищами взрывается цилиндрический заряд длиной тротила плотностью ρ₀ = = 1,6 г/см³, теплотой взрыва Q₀ = 4200 кДж/кг. Заряд ВВ (5 кг/пог. м) расположен строго по оси камеры так, что торец его перекрывает сечение стыковки днища с обечайкой в направлении днища на . Определить частоту и период колебаний, величину смещений, скорости смещений, ускорения движения и напряжения в элементах оболочки камеры.