53

Общие сведения

Тематика практических работ направлена на закрепление и углубление теоретических знаний, полученных студентами на лекциях, и выработку умений и навыков в выполнении оценок, физических и технологических расчетов по высокоэнергетическим методам получения малых частиц. По дисциплине запланированы практические занятия в объеме 17 часов (табл. 1).

Практические занятия способствуют формированию следующих компетенций:

инструментальных компетенций (ИК):

ИК-5 - умение проводить расчеты и делать выводы;

общепрофессиональных компетенций (ОПК):

ОПК-2 - моделировать физические, химические и технологические процессы;

ОПК-3 - прогнозировать свойства материалов и эффективность процессов;

специальных профессиональных компетенций (СПК):

СПК-1 - умение разрабатывать технологические процессы;

СПК-6 - умение осуществлять выбор материалов для изделий различного назначения с учетом эксплуатационных требований;

СПК-8 - умение анализировать технологический цикл получения и обработки материалов.

Преподаватель, ведущий практические занятия, формирует индивидуально для каждого студента 3 комплекта по 5 задач. Выдача заданий и их защита осуществляется в соответствии с графиком учебного процесса и самостоятельной работы студентов по дисциплине, либо в близкие сроки, установленные преподавателем, во время практических занятий или в другое время, назначенное преподавателем. Задачи оформляются по требованиям, предъявляемым к оформлению задач по курсу общей физики.

1. Содержание практических занятий

Содержание практических занятий отражено в табл. 1.

Таблица 1

№ п/п	Номер раздела дисциплины	Темы занятий (трудоемкость)
1	Раздел 1	Высокоэнергетические методы воздействия на материалы (2 часа – 0,06 з. е.)
2	Раздел 2	Ударно-волновой синтез. Детонационный синтез. Термодинамика превращения. Состав продуктов взрыва (4 часа – 0,11 з. е.)
3	Раздел 2	Взрывчатые вещества и их состав. Свойства ВВ и кислородный баланс (2 часа – 0,06 з. е.)
4	Раздел 2	Свойства ВВ и кислородный баланс (2 часа – 0,06 з. е.)
5	Раздел 2	Взрывные камеры и расчет основных характеристик (4 часа – 0,33 з. е.)
6	Раздел 3	Перспективы развития методов получения и областей применения наноматериалов (3 часа – 0,08 з. е.)

Примеры решения задач

20. Вычисляем молярный вес вещества по уравнению состояния идеального газа , где m – масса исследуемого вещества;  – молярная масса исследуемого вещества; R – универсальная газовая постоянная.

Имея формулу соединения в общем виде и используя данные о его молярной массе и весовом соотношении входящих в него элементов, составляем три уравнения:

z·16 + z·16·0,375 + z·16·2,25 = 116;

y·1 = z·16·0,375;

x·12 = z·16·2,25,

где 16, 1, 12 – атомные веса О, Н и С соответственно. Решение уравнений дает: z = 2, y = 12, x = 6 и С_xН_yО_z = С₆Н₁₂О₂.

34. Так как плотность воздуха  зависит от высоты z, столб воздуха нельзя считать однородной системой. Тем не менее в состоянии теплового равновесия температура Т должна быть однородной. Если неоднородную систему можно разбить на такие части (подсистемы), что каждую из них допустимо считать однородной, а взаимодействие между ними пренебрежимо малым, то энергия полной системы будет равна сумме энергий ее частей. Цилиндрический объем, лежащий между z и z+dz, можно считать однородной подсистемой такого рода с внутренней энергией и потенциальной энергией , где S – площадь поперечного сечения цилиндра, – внутренняя энергия единицы массы воздуха, рассматриваемого как идеальный газ, a g – ускорение силы тяжести. Так как суммарная энергия слоя, лежащего между z и z+dz, равна , то полная энергия всего воздуха в цилиндрическом объеме от до имеет вид

Зависимость  от высоты определяется уравнением . Чтобы исключить p(z), продифференцируем уравнение состояния ; тогда

,

откуда

,

или

.

Вместо плотности воздуха (0) вблизи поверхности Земли при z = 0 удобнее ввести полную массу воздуха в цилиндрическом объеме:

,

что дает

.

С помощью этого соотношения получаем энергию рассматриваемого объема воздуха:

.

Отсюда видно, что энергия является функцией только температуры. Теплоемкость определяется выражением

Воспользовавшись соотношением Майера , получаем

.

47. Находящиеся в воде частицы УДА испытывают действие архимедовой подъемной силы. Тогда эффективная масса (масса частицы за вычетом массы жидкости в объеме частицы) равна .

При вращении цилиндра на частицы действует центробежная сила инерции . Чтобы переместить частицу из периферийной области в точку, находящуюся на расстоянии r от оси, необходимо затратить энергию

.

Обозначим через N_o плотность числа частиц (плотность распределения) на периферии (r = r₀ ). Тогда в соответствии с законом распределения Больцмана можно записать

,

где N(r) – плотность распределения числа частиц на расстоянии r от оси цилиндра, k – постоянная Больцмана.

Отношение .

Подставив числовые данные, получим

.

Таким образом, плотность распределения УДА на периферии в 67 раз больше плотности на оси.

62. Используя соотношения:

,

получаем, что или . Кроме того, известно, что и

Таким образом мы пришли к искомому результату.

68. В системе отсчета, в которой тело покоится, течение газа можно считать стационарным. Уравнение Бернулли в этой системе запишем в виде . Температура максимальна в точке, где v = 0. Она равна

,

или

,  

где  – число Маха (c_зв – скорость звука).

69.  Скорость испарения определяется выражением

,

где n – концентрация атомов насыщенного пара вольфрама. Его давление будет

.

При максвелловском распределении

где  – относительная атомная масса, равная для вольфрама 184. Окончательно получаем

.

Подставив сюда численные значения, найдем для давления насыщенных паров вольфрама при Т = 2000 К: Р = 8,610^–9 дин/см² = 6,410^–12 мм рт. ст.

73. При изотермическом растяжении к пленке надо подводить тепло. Пусть – удельная теплота образования пленки при изотермическом растяжении. По первому началу термодинамики

.

Свободная энергия пленки , тогда . Отсюда следует

.

С учетом и определения q получаем

Если процесс образования пленки изотермический, то согласно полученному соотношению . Таким образом, при изотермическом увеличении поверхности пленки . За параметры, определяющие состояние пленки, можно принять площадь A и температуру Т. Энергия, приходящаяся на единицу поверхности пленки, от величины A не зависит. Поэтому

.

74. При адиабатическом расширении . Элементарное изменение внутренней энергии

Так как , где c_A – теплоемкость единицы поверхности пленки при постоянном значении A, и , получаем

.

Таким образом, при адиабатическом расширении пленка охлаждается.

75. Считая (c_V – удельная теплоемкость воды), получаем

.

Коэффициент «2» учитывает то обстоятельство, что пленка – двухсторонняя.

88. Капля примет форму диска с вогнутой периферийной поверхностью. Кривизной сечения этой поверхности плоскостью, параллельной пластинкам, можно пренебречь. Радиус кривизны нормального к нему сечения . Средняя кривизна боковой поверхности диска

.

Давление жидкости между дисками меньше атмосферного на . Площадь диска , где  – плотность жидкости. Пластинки будут прижиматься друг к другу с силой

.

93. Обозначим через и удельные свободные энергии Гиббса вещества в этих фазах. Свободная энергия Гиббса , ее приращение для элементарного квазистатического процесса , где u, s, v – удельные энергия, энтропия и объем. При смещении вдоль кривой испарения или

Последнее соотношение запишем в виде

.

Фазовые превращения, вообще говоря, сопровождаются выделением или поглощением тепла. Например, при переходе единицы массы вещества из газообразного состояния в жидкое выделяется тепло

.

При обратном переходе из жидкого состояния в газообразное такое же тепло поглощается. Предполагается, что переход совершается квазистатически при постоянной температуре, а следовательно, и при постоянном давлении. Тепло q называется удельной теплотой парообразования или испарения. В общем случае оно называется удельной теплотой фазового превращения (плавления, возгонки и т. п.). Таким образом,

.

Это соотношение называется уравнением Клапейрона – Клаузиуса.

98. Удельная теплота возгонки q = q₁ + q₂ = 676 кал/г. Подставляя формулу в уравнение Клапейрона – Клаузиуса

и определяя удельный объем водяного пара из уравнения , легко найти, что при Т = –1 К P = 0,38 мм рт. ст., а давление насыщенного пара над льдом при t = –1 С равно P_–1 С = 4,20 мм рт. ст.

105. Для приближенной оценки в уравнении

заменим производную dP/dT отношением конечных приращений. Получим

где P₁ и P₂ – давления насыщенного пара при температурах Т₁ и T₂. Давление пара в воздухе при температуре Т₁ и относительной влажности f будет fP₁, а потому . Подставляя эти значения в предыдущее соотношение, находим

.

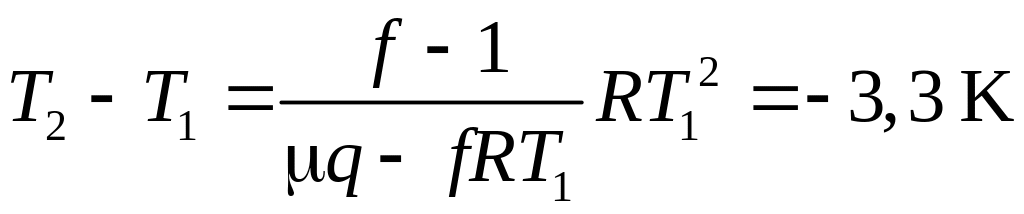109. Стационарный поток пара через любую сферическую поверхность радиуса r, концентрическую относительно поверхности капли, равен

,

откуда

.

Величину q можно найти из условия, что на поверхности капли (r = a) пар должен быть насыщенным. Это дает

,

где  – относительная молярная масса пара, Р_н – давление насыщенного пара при температуре капли жидкости, Р_ – парциальное давление паров жидкости вдали от капли. Подставляя значение q в предыдущую формулу, получаем

.

112. Применив термохимическую символику (фигурные скобки – газ, круглые – жидкость, квадратные – твердое вещество), запишем:

,

Исключая {СО₂}, находим

Отсюда .

120. Если таяние льда идет не очень быстро, то мгновенное распределение температуры в окружающей воде будет таким же, что и в стационарном случае при тех же граничных значениях температуры. Оно в рассматриваемом случае имеет вид

,

где R – мгновенное значение радиуса куска льда, Т₀ и T_ – постоянные температуры воды на поверхности шара и в бесконечности (по условию задачи Т₀ – T_ = 10 С). Количество тепла, поступающее к шару от окружающей среды за время dt, равно

.

Это тепло идет на расплавление льда и потому может быть также представлено выражением

.

Приравнивая оба выражения, получаем

.

Отсюда интегрированием находим искомое время таяния льда:

.

121. Обозначим буквой х толщину образовавшегося слоя льда к моменту времени t. Если замерзание идет не очень быстро, как это в действительности имеет место в естественных условиях, то в слое льда установится линейное падение температуры от T_пл до T. В этом случае тепло, уходящее наружу от единицы поверхности льда за время dt, определим по выражению

Но ту же величину можно представить в виде , где dx – толщина слоя льда, образовавшегося за время dt;  – плотность льда; q – удельная теплота плавления льда. Получаем уравнение

.

Умножая x и интегрируя, находим

.

Примем за начало отсчета времени момент, когда образование льда на поверхности воды только что началось. Тогда x = 0 при t = 0, а потому A = 0. В результате получим

.

122. Рассмотрим тепловой баланс в объеме стержня между сечениями х и x + dx. Слева за время d входит количество тепла – . Справа выходит – . Кроме того, благодаря теплообмену из объема через его боковую поверхность уходит тепло . Тепло, поступившее в рассматриваемый объем стержня, равно . Итак,

.

Отсюда

.

137.

1. Частота

2. Период колебаний

3. Время действия давления за отраженной ударной волной

4. Отношение времени действия давления за отраженной ударной волной к периоду колебаний оболочки равно

5. Период циркуляции упругой волны

6. Радиальные максимальные смещения

7. Максимальная скорость радиальных смещений

Здесь приведенный радиус заряда r₀ определяется из формулы

8. Максимальные радиальные ускорения движения стенки оболочки камеры

9 . Напряжения в толщине оболочки (радиальные)

Здесь берем для продуктов взрыва равную трем.

10. Касательные напряжения в оболочке

11. Эквивалентные напряжения в материале оболочки

=

12. Максимальная скорость деформирования материала оболочки равна

13. Динамический предел текучести для наших условий при

равен

Отсюда видно, что эквивалентные напряжения меньше динамического предела текучести,

Ускорения движения стенки оболочки для случая цилиндрической оболочки

138.

1. Частоту определим по формуле для обечайки:

Период колебаний

Для днища:

=

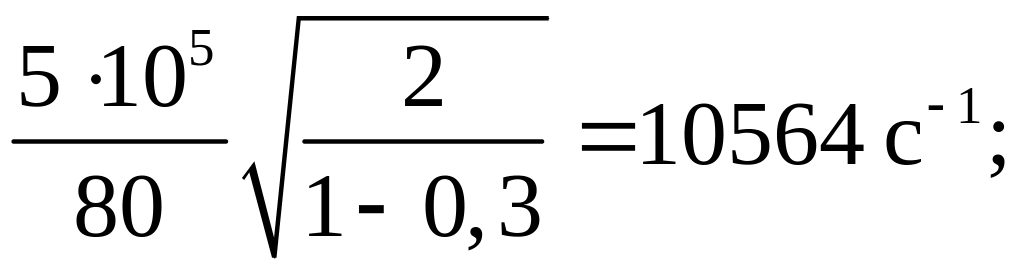
2. Радиальные смещения обечайки

где

Радиальные смещения у днища

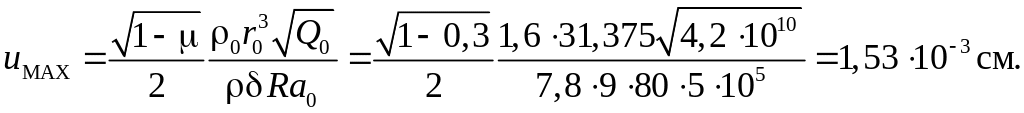
3. Скорость смещений обечайки

Максимальная радиальная скорость смещений у днища

4. Максимальные ускорения движения обечайки камеры

Максимальные ускорения движения у днища камеры

5. Радиальная компонента равна , которую найдем из формулы , . Учитывая, что для цилиндрического случая , получаем:

Касательная компонента тензора напряжений для цилиндрической оболочки

Цилиндрическая компонента (напряжения вдоль образующей обечайки камеры) равна сферической компоненте или . Ее найдем с учетом того, что импульс взрыва, действующий на полусферическое днище, есть импульс цилиндрического заряда длины Таким образом, только эта часть заряда создает импульс давления на полусферическое днище цилиндрической камеры:

.

Сферическая компонента

6. Мы видим, что сферические радиальные напряжения на порядок меньше цилиндрических. Поэтому их можно не учитывать при определении полных эквивалентных напряжений.

7. Максимальная скорость деформирования материала обечайки = , а материала днища

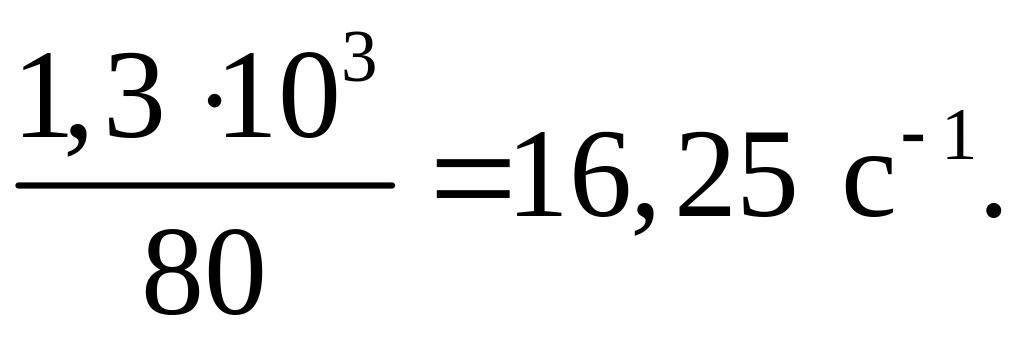
Для наших условий . Тогда – для обечайки и = = – для днища.

8. Коэффициент запаса прочности – для обечайки и – для днища.

Задача решена в полном объеме.