Лабораторная работа № 2. Интерполяция

Цель работы: научится применять интерполяционные многочлены

Интерполяция — способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.

Многим из тех, кто сталкивается с научными и инженерными расчётами часто приходится оперировать наборами значений, полученных экспериментальным путём или методом случайной выборки. Как правило, на основании этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Такая задача называется аппроксимацией кривой. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных.

Р

(2.1)

ассмотрим систему несовпадающих точек из некоторой области D. Пусть значения функции f известны только в этих точках:

З

(2.2)

адача интерполяции состоит в поиске такой функции F из заданного класса функций, что

• Точки называют узлами интерполяции, а их совокупность — интерполяционной сеткой.

• Пары называют точками данных или базовыми точками.

• Разность между «соседними» значениями  — шагом интерполяционной сетки. Он может быть как переменным, так и постоянным.

• Функцию F(x) — интерполирующей функцией или интерполянтом.

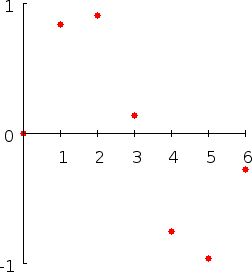
Рис. 2.1

Точки данных (из приведённой таблицы), в декартовой системе координат.

1. Пусть мы имеем табличную функцию, наподобие описанной ниже, которая для нескольких значений x определяет соответствующие значения f:

	0	1	2	3	4	5	6
	0	0.8415	0.9093	0.1411	-0.7568	−0,9589	−0,2794

Табл. 2.2

Интерполяция помогает нам узнать какое значение может иметь такая функция в точке, отличной от указанных, например, при x = 2,5?

2. Найти промежуточное значение

6000	15.5
6378	?
8000	19.2

Табл. 2.3

(2.3)

Интерполяция многочленами

На практике чаще всего применяют интерполяцию многочленами. Это связано, прежде всего, с тем, что многочлены легко вычислять, легко аналитически находить их производные и множество многочленов плотно в пространстве непрерывных функций (теорема Вейерштрасса).

Кусочно-линейная интерполяция.

При решении ряда задач требуется восстановить функцию y=f(x) для произвольного значения x на отрезке [a,b], если известны ее значения в некотором конечном числе точек этого отрезка (найденных, например, в результате эксперимента). Кроме того, функция y=f(x) может быть задана формулой, вычисление значений которой очень трудоемко, например:

(2.4)

и требуется иметь для f(x) более простую формулу, которая позволяла бы находить значения f(x) в любой точке с заданной точностью e. Данная задача решается путем интерполяции.

Математическая постановка.

Пусть известные значения некоторой функции y=f(x) образуют на отрезке [a,b] следующую табличную функцию:

x	x0	x1	...	xN
f	f0	f1	...	fN

Табл. 2.4

Табличная функция.

где a ≡ x₀ < x₁ < ... < x_N ≡ b.

Т

(2.5)

ребуется построить интерполянту - функцию F(x), совпадающую с f(x) в точках x_i:

F(xi ) = fi , i=0, ..., N

Нахождение функции-интерполянты F(x) называют интерполяцией, а точки x₀ , x₁ , ... , x_N - узлами интерполяции. Величины h_i=x_i - x_i-1 , i = 1, ..., N - называют шагами табличной функции.

Так как основная цель интерполяции - получить быстрый алгоритм вычисления значений F(x) для xÎ[a,b], не содержащихся в таблице данных,

Простейшим видом интерполяции является кусочно-линейная интерполяция.

Кусочно-линейная интерполяция состоит в том, что заданные точки (x_i , f_i ), i = 0, ..., N соединяются прямолинейными отрезками, и функция f(x) приближается полученной ломаной.

(2.6)

Уравнения каждого отрезка ломаной в общем случае разные. Поскольку имеется N интервалов (x_i-1 , x_i), то для каждого их них в качестве уравнения интерполянты используется уравнения прямой, проходящей через две точки. В частности, для i-го интервала можно написать уравнение прямой, проходящей через точки (x_i-1 , f_i-1 ) и (x_i , f_i ), в виде

(y - f_i-1 )/(f_i - f_i-1 ) = (x - x_i-1 )/(x_i - x_i-1 )

Отсюда

y = aix + bi ≡ F(x), x (xi-1, xi) ai = (fi - fi-1 )/(xi - xi-1 ), bi = fi-1 - aixi-1 , i = 1, ..., N

Следовательно, при использовании кусочно-линейной интерполяции сначала нужно определить номер i интервала, в который попадает значение аргумента x, затем подставить x и i в формулу (3.2) и найти приближенное значение функции в точке x.

Е

(2.7)

сли f(x) C ² [a, b], то оценка погрешности при кусочно-линейной интерполяции имеет вид

|f(x) - F(x)| ≤ M₂ h²/2,

где Линейная интерполяция.

Линейная интерполяция состоит в том, что заданные точки М(x_i, y_i) (i = 0, 1, ..., n) соединяются прямолинейными отрезками, и функция f(x) приближается к ломаной с вершинами в данных точках

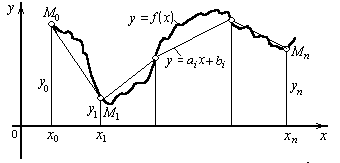
Рис. 2.2

У

(2.8)

равнения каждого отрезка ломаной линии в общем случае разные. Поскольку имеется n интервалов (x_i , x_{i + 1}), то для каждого из них в качестве уравнения интерполяционного полинома используется уравнение прямой, проходящей через две точки. В частности, для i - го интервала можно написать уравнение прямой, проходящей через точки (x_i , y_i) и (x_i + 1, y_i + 1), в виде:

Отсюда

Следовательно, при использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение аргумента x, а затем подставить его в формулу и найти приближенное значение функций в этой точке.

 

Квадратичная интерполяция

В случае квадратичной интерполяции в качестве интерполяционной функции на отрезке (x_{i - 1},x_{i + 1}) принимается квадратный трехчлен.

У

(2.9)

равнения квадратного трехчлена

y = aix2 + bix + ci,, xi – 1 x xi + 1,

содержат три неизвестных коэффициента a_i, b_i, c_i, для определения которых необходимы три уравнения.

Ими служат условия прохождения параболы через три точки (x_{i - 1}, y_{i - 1}), (x_i, y_i), (x_{i + 1}, y_{i + 1}). Эти условия можно записать в виде:

Интерполяция для любой точки проводится по трем ближайшим точкам.

Контрольные вопросы:

1.Что такое интерполяция?

2.В чем состоит принцип кусочно-линейной интерполяции?

3. В чем состоит принцип линейной интерполяции?